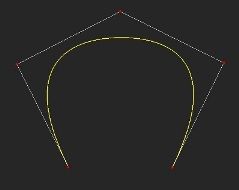
B-Spline knot insertion

B-Spline knot insertion

 

 

 

这里给大家介绍二个B-Spline曲线很重要的基本算法，knot insertion和knot refinement。Knot insertion就是指增加曲线knot个数，或者说改变曲线的knot vector空间，但是不改变曲线的形状。knot refinement指重定义曲线的knot vector，在每两个knot之间插入一个新的knot，同样不改变曲线的形状。这两种算法都可以增加曲线灵活性。一个B-Spline曲线，控制点越多曲线就可以进行更加细部的形状改变。

 

          

 

     图1                                                        图2

          

 

    图3                                                       图4

 

上面4幅图中是一条三次B-Spline曲线，图1是原始曲线，图3是经过2次knot refinement的曲线，曲线的形状没有改变，控制点由原来的5个增加为knot refinement后的11个。图2是在原始曲线上移动一个控制点后，曲线形状的改变。图4是knot refinement后移动控制点曲线形状的改变。从图2和图4中明显可以看出控制点多的曲线在改变形状是更为灵活。下面就开始介绍knot insertion和knot refinement算法。

 

knot insertion

 

一条B-Spline曲线的knot增加后，我们来看看它有什么变化。假设有一曲线

 

 

 

 

定义在上。现在有一个新的knot， ，我们现在把这个knot插入到现有的U中，于是可以得到新的knot空间，我们把新的knot记为，那么有

 

 

 

 

曲线的knot增加后，于是可以写成

 

 

 

 

 

 

为knot增加后的曲线的控制点。注意到，knot添加前和knot添加后曲线的形状是没有改变的，也就是说，曲线上的点是没有变化的，所以有

 

 

 

 

进一步可以得到

 

 

 

 

如果把上面这个公式展开，可以得到一个线性方程组。对于所有的u，当 时，很明显

 

 

 

 

而对于原来曲线和knot添加后曲线的控制点，有

 

 

 

 

 

当i=k-p，…，k时，有下面的公式

 

 

 

曲线每当添加一个knot后，它的控制点也要增加一个。所以，当曲线的knot增加后，实际上就转化为了求knot增加后的曲线的控制点的问题。有了上面knot增加前的基函数和knot增加后的基函数的关系，就可以推导出knot在增加前后控制点之间的关系。实际上，它们之间是通过线性插值来得到的。现在只给出公式

 

 

 

 

现在看个例子。

 

曲线次数p=3次，U={0，0，0，0，1，2，3，4，5，5，5，5}。控制点为P0,P2,…P7。现在增加一个knot u=2.5，求出knot增加后的所有控制点Qi。

 

因为要添加u=2.5， 所以u在[u5，u6]之间，那么k=5。根据上面的公式有

 

 

同样的道理可以求出所有控制点。只要知道了控制点的位置和新的knot，就可以得到新的knot添加后的曲线了。

 

Knot refinement

 

只要实现了knot的添加操作，要实现knot refinement就比较简单了。Knot refinement就是在已有的所有knot之间的中点处插入新的knot。比如：

U={ 0，0，0，0，1，2，3，4，5，5，5，5 }

那么进行一次knot refinement后，就变为

U={ 0，0，0，0，0.5，1，1.5，2，2.5，3，3.5，4，4.5，5，5，5，5 }

Knot增加了5个，相应的控制点也增加5个。有了上面knot insertion的算法，要进行knot refinement的话，只需要找出原来knot的间隔，然后在每个间隔进行一次中点knot insertion就可以了。

 

*原创文章，转载请注明出处*