POJ 2398 Toy Storage【叉积+二分】

链接:

http://poj.org/problem?id=2398

http://acm.hust.edu.cn/vjudge/contest/view.action?cid=29328#problem/E

Toy Storage

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 3344		Accepted: 1924

Description

Mom and dad have a problem: their child, Reza, never puts his toys away when he is finished playing with them. They gave Reza a rectangular box to put his toys in. Unfortunately, Reza is rebellious and obeys his parents by simply throwing his toys into the box. All the toys get mixed up, and it is impossible for Reza to find his favorite toys anymore. 
Reza's parents came up with the following idea. They put cardboard partitions into the box. Even if Reza keeps throwing his toys into the box, at least toys that get thrown into different partitions stay separate. The box looks like this from the top: 

We want for each positive integer t, such that there exists a partition with t toys, determine how many partitions have t, toys.

Input

The input consists of a number of cases. The first line consists of six integers n, m, x1, y1, x2, y2. The number of cardboards to form the partitions is n (0 < n <= 1000) and the number of toys is given in m (0 < m <= 1000). The coordinates of the upper-left corner and the lower-right corner of the box are (x1, y1) and (x2, y2), respectively. The following n lines each consists of two integers Ui Li, indicating that the ends of the ith cardboard is at the coordinates (Ui, y1) and (Li, y2). You may assume that the cardboards do not intersect with each other. The next m lines each consists of two integers Xi Yi specifying where the ith toy has landed in the box. You may assume that no toy will land on a cardboard. 

A line consisting of a single 0 terminates the input.

Output

For each box, first provide a header stating "Box" on a line of its own. After that, there will be one line of output per count (t > 0) of toys in a partition. The value t will be followed by a colon and a space, followed the number of partitions containing t toys. Output will be sorted in ascending order of t for each box.

Sample Input

4 10 0 10 100 0
20 20
80 80
60 60
40 40
5 10
15 10
95 10
25 10
65 10
75 10
35 10
45 10
55 10
85 10
5 6 0 10 60 0
4 3
15 30
3 1
6 8
10 10
2 1
2 8
1 5
5 5
40 10
7 9
0

Sample Output

Box
2: 5
Box
1: 4
2: 1

Source

Tehran 2003 Preliminary

题意：

给你 N 个木块的位置，保证各个木块的放置不交叉。这样就形成了 N 个小格子。

再给你 M 个点的坐标，让你确定点在第几个格子里面。

输入注意：第一行 N 表示有 N 块木板

           M，(x1, y1) (x2, y2) 分别表示有 M 个点。

           第一个点 (x1, y1) 代表格子左上角的点，第二个点 (x1, y2) 代表格子右下角的点

           然后是 N 行的输入：每一行 Ui 和 Li 确定一个木板的位置 (Ui, y1)—— (Li, y2)

           注意：木板的输入不是按照顺序的。。。

                   

           下面的 M 行：每个点的坐标

输出注意：具体格式看样例。

按照点的个数由小到大的顺序输出：点的个数 和 包含了相应的点的方框的个数

比如说第一组样例输出：表示包含了 2 个点的格子有 5 个

第二组样例输出： 表示包含了 1 个点的格子有 4 个

                包含了 2 个点的格子有 5 个

算法：叉积+二分

思路：

先对木块按照从左到右排序,确立每个格子。

然后每次输入一个点，就用叉积判断它属于哪个格子。

如何判断属于哪个格子？

如果我们能找到一个点右边的距离它最近的木块，排序后此木块编号为 index 那么就说明,当前点在第 index 个格子里面，这一点没有问题吧。

如何判断一个点在一条线段的左边还是右边？

叉积处理：Cross(V1, V2) 表示向量 V1 和 V2 的叉积，注意方向问题和叉积处理的顺序。

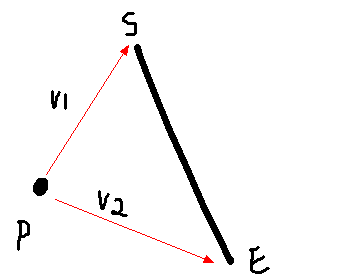
如图所示如果点 P 在线段 SE 左边，那么 Cross(V1, V2) < 0

反之如果在右边 ，那么Cross(V1,V2) > 0这个不明白就自己画下图。

那么解决了点和线段的相对位置问题，那么如何快速判断，注意已经排序好了，简单二分处理下就可以快速找到相应线段。

code：

#include<stdio.h>
#include<string.h>
#include<iostream>
#include<algorithm>
using namespace std;

const int maxn =5050;
int ans[maxn];
int num[maxn];

struct Point{
    int x;
    int y;

    Point() {}
    Point(int _x, int _y){
        x = _x;
        y = _y;
    }

    Point operator -(const Point &b) const {
        return Point(x-b.x, y-b.y);
    }

}p[maxn];

struct Line {
    Point s;
    Point e;

    Line() {}
    Line(Point _s, Point _e){
        s = _s;
        e = _e;
    }
}line[maxn];

int Cross(Point a, Point b)
{
    return a.x*b.y - b.x*a.y;
}


bool cmp(Line a,Line b)
{
    return a.s.x < b.s.x;
}

int main()
{
    int n, m;
    int x1,y1,x2,y2;
    while(scanf("%d", &n) != EOF)
    {
        if(n == 0) break;
        scanf("%d%d%d%d%d", &m,&x1,&y1,&x2,&y2);

        int Ui, Li;
        for(int i = 0; i < n; i++)
        {
            scanf("%d%d",&Ui,&Li);
            line[i] = Line(Point(Ui,y1), Point(Li,y2));
        }
        line[n] = Line(Point(x2,y1), Point(x2,y2)); //

        sort(line,line+n+1,cmp);
        memset(ans, 0, sizeof(ans));
        int temp;
        int Xj,Yj;
        for(int i = 0; i < m; i++)
        {
            scanf("%d%d", &Xj,&Yj);
            Point p = Point(Xj,Yj);
            int left = 0;
            int right = n;
            int mid;
            while(left <= right)
            {
                mid = (left+right)/2;
                Point p1 = line[mid].s; Point p2 = line[mid].e;
                if(Cross(p1-p, p2-p) < 0) //点 p 在线段p1-p2 右边
                {
                    temp = mid;
                    right = mid-1;
                }
                else left = mid+1;
            }
            ans[temp]++;
        }

        memset(num,0,sizeof(num));
        for(int i = 0; i <= n; i++)
            if(ans[i] > 0) num[ans[i]]++;
        printf("Box\n");
        for(int i = 1; i <= n; i++) //ans[i] <= n
            if(num[i] > 0) printf("%d: %d\n", i, num[i]);
    }
    return 0;
}