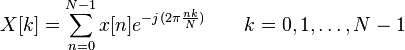快速傅立叶变换FFT

理论

FFT的作用就不多说了，搞信号处理的人都会用上。

FFT的由来：傅立叶变换FT、离散傅立叶变换DFT、快速傅立叶变换FFT。

学习资料：

1、陈后金的《数字信号处理》，里面深入浅出，该有的公式都有，编程思想也有。

2、一篇系统讲述傅立叶变换的帖子：http://blog.csdn.net/v_JULY_v/article/details/6196862

3、学生对FFT的理解：http://tieba.baidu.com/p/2513502552

4、工程人员对FFT的简单明了的总结：http://blog.jobbole.com/58246/

5、英文版的阐述：http://cnx.org/contents/bcb1664b-931d-4055-bcc2-9bbbf94becfd@8/The_Fast_Fourier_Transform_(FF

6、维基：http://zh.wikipedia.org/wiki/库利－图基快速傅里叶变换算法

7、一篇碉堡了的博文：http://blog.jobbole.com/70549/

FFT就是DFT的快速算法，最经典的形式莫过于Cooley-Tukey算法，除此之外有多种变体，直到今天依然有人研究。

Cooley-Tukey算法就是基2-FFT，其基本思想是分治，把原始数据的奇偶项分成两部分，并一直分裂直到剩下一个，通过这样做，将DFT的复杂度 O(n^2)降为O( n*log2(n) )

这样做的原理是公式推导发现前半部分和后半部分的表达式是共轭对称的，只需要做前半部分的运算。

以下是将原始数据进行分裂的图示：

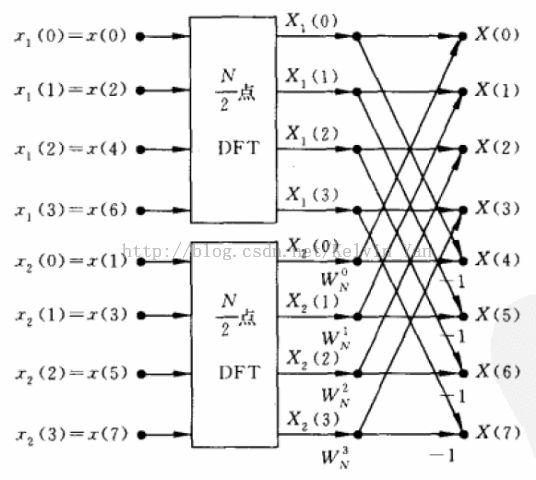
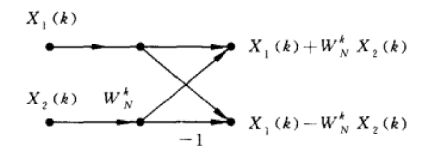
8点的原始数据按 0、2、4、6 和 1、3、5、7 的奇偶顺序划分为两部分，前半部分作为余弦分量，后半部分作为正弦分量，对应相加，这又被称为蝶形运算，如下图：

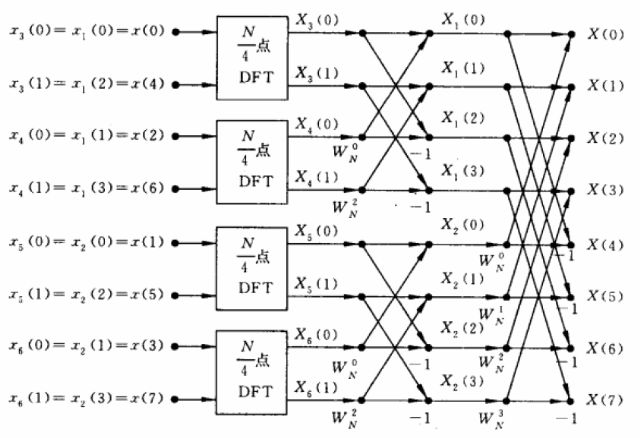
上面的两部分，各自又可以继续分解，变成：

到这里，8点的DFT就被分解为3次的蝶形运算组合。如果按照DFT的公式

计算，将要进行N^N次循环，k和n均为[0,,N-1]的循环变量，而采用FFT则只需要进行N*log2(N)次循环，外层循环为log2(N)次分解，内层循环为N个数据点运算

FFT的对称性

实信号的频谱时共轭对称的，对于实序列同样成立。由DFT定义可以验证。
DFT定义：X(k)=Sigma(x(n)*exp(2*pi*k*n/N)),式中N为序列长度，求和限为n=0,1,...,N-1；结果k的取值范围为k=0,1,...,N-1。(FFT为DFT的快速算法)
这里序列序号从0到N-1,有时是从1到N，注意区别。
由此可知，X(0)=Sigma(x(n))。如果x(n)为实序列，X(0)就一定是实的，代表的是序列的直流(零频)分量。n取1和N-1,2和N-2,...时，由exp(.)指数函数的性质可以分析得到DFT序列的对称性。共轭对称的一个直接结果就是零频两侧对称的部分幅度相等【DFT直接得到的是[0,2*pi]区间，根据数字频率的2*pi周期性，可把[pi,2*pi]等价到[-pi,0]区间】。
关于DFT的对称性，数字信号处理的书籍均有介绍，可参考：
1.丁玉美。《数字信号处理》，西电出版
2.奥本海姆，《离散时间信号处理》（第二版），西安交大出版

 编程

DFT

根据该公式编写循环： 

用欧拉公式进行复数运算：

 

为了方便直接在matlab上进行数据的生成和显式，VC负责DFT，代码如下：

inputData.m，产生输入数据

pi = 3.141526;  

%% 产生原始数据

N = 4096;      %采样点数
fs = 5000;    %采样频率
Ts = 1/fs;     %采样周期

t = 0:Ts:(N-1)*Ts;  %采样范围
xr = sin(2*pi*100*t)+sin(2*pi*750*t);       %100Hz、750Hz的正弦波
xr = xr + randn(size(t)); %加噪声

plot(t,xr);
axis([t(1),t(100),1.1*min(xr),1.1*max(xr)]);

xi = zeros(1,N);
x(1:N) = double(xr);
x(N+1:2*N) = double(xi);

% %matlab 的 fft函数
% X = fft(x,N);
% r = abs(X);
% f = fs*linspace(0,1,N); 
% plot(f,r)
% grid on
% maxx = find(r==max(r));
% text(f(maxx(1)),max(r),['max=',num2str(f(maxx(1)))]);

fid = fopen('inputData.dat','wb');
if(fid)
    fwrite(fid,x,'float64');
else
    msgbox('保存失败');
end
fclose(fid);

DFT.cpp，控制台程序

// DFT.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include "math.h"
#include "iostream"
#include <fstream>

using namespace std;

void DFT(double *x, double *X, int N);

int _tmain(int argc, _TCHAR* argv[])
{
	//初始化参数
	int N = 4096;
	double *x= new double[N*2]; //前N点是实部,后N点是虚部
	double *X= new double[N*2];

	//从外部读取数据
	ifstream mfile;
	mfile.open("I:\\project\\FFT\\Debug\\inputData.dat", ios::in|ios::binary); 	
	mfile.read ((char*)x, N*2*sizeof(double));	
	mfile.close();

	//DFT
	DFT(x,X,N);
	
	//向外输出数据
	ofstream mfile1;
	mfile1.open("I:\\project\\FFT\\Debug\\outputData.dat", ios::out|ios::binary);	
	mfile1.write((const char*)X, N*2*sizeof(double));	
	mfile1.close();

	//释放内存
	delete [] x;
	delete [] X;

	return 0;
}

void complexMul(double re0, double im0, double re1, double im1, double *pre, double *pim)
{
	*pre = re0*re1 - im0*im1; //实部
	*pim = re0*im1 + re1*im0; //虚部
}

// DFT
// x原始数据，X变换数据
// N为数据的采样点数
void DFT(double *x, double *X, int N)
{
	const double pi=3.141526;

	double *xr = x;											//时域
	double *xi = x+N;
	double *Xr = X;											//频域
	double *Xi = X+N;

	int k,n;												//循环变量
	double tr,ti,br,bi,sumr,sumi;							//中间变量

	for(k=0;k<N;k++)
	{
		sumr=0;
		sumi=0;												//累加清零

		for(n=0;n<N;n++)
		{
			br = cos(2*pi*n*k/N);
			bi = -sin(2*pi*n*k/N);							//计算e指数部分
			complexMul(xr[n], xi[n], br, bi, &tr, &ti);		//输入数据乘上e指数部分
			sumr = sumr + tr;								
			sumi = sumi + ti;								//累加
		}

		Xr[k] = sumr;
		Xi[k] = sumi;										//第k个频率分量
	}
}

outputData.m，显式结果

%% 打开dat文件
N=4096;
fid = fopen('outputData.dat','rb');
if(fid)
    X = fread(fid,N*2,'float64');
else
    msgbox('打开失败');
end
fclose(fid);

Xr = X(1:N);
Xi = X(N+1:2*N);

r = sqrt(Xr.^2 + Xi.^2);
fs = 5000;
f = fs*linspace(0,1,N); 
plot(f,r)
grid on
maxx = find(r==max(r));
text(f(maxx(1)),max(r),['max=',num2str(f(maxx(1)))]);

当然也可以在opencv中画频谱图——matlab风格的plot函数：http://www.360doc.com/content/14/0424/12/16961511_371675228.shtml

基2-FFT

输入数据和输出数据依然采用上面的inputData.m和outputData.m

FFT.cpp，控制台程序：

// FFT.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include <math.h>
#include <complex>
#include "iostream"  
#include <fstream> 

#include "ref.h"

using namespace std;

void FFT(complex<double>*TD,complex<double>*FD,int r);//r为log2N，即迭代次数  

int _tmain(int argc, _TCHAR* argv[])
{
	//初始化参数  
    int N = 4096;  
    double *x= new double[N*2]; //前N点是实部,后N点是虚部  
    double *X= new double[N*2];  
  
    //从外部读取数据  
    ifstream mfile;  
    mfile.open("inputData.dat", ios::in|ios::binary);    
    mfile.read ((char*)x, N*2*sizeof(double));    
    mfile.close();

	//FFT
	complex<double>*TD = new complex<double> [N];
	complex<double>*FD = new complex<double> [N];
	for(int i=0;i<N;i++)
	{
		TD[i].real(x[i]);
		TD[i].imag(x[i+N]);
	}
	FFT(TD,FD,12);
	for(int i=0;i<N;i++)
	{
		X[i] = FD[i].real();
		X[i+N] = FD[i].imag();
	}

	//向外输出数据  
    ofstream mfile1;  
    mfile1.open("outputData.dat", ios::out|ios::binary);     
    mfile1.write((const char*)X, N*2*sizeof(double));     
    mfile1.close();  
  
    //释放内存  
    delete [] x;  
    delete [] X;

	return 0;
}

void FFT(complex<double>*TD,complex<double>*FD,int r)//r为log2N，即迭代次数  
{  
	const double PI = 3.141526;
    long    count;              // 付立叶变换点数    
    int     i,j,k;              // 循环变量  
    int     bfsize,p;     
    double  angle;              // 角度     
    complex<double> *W,*X1,*X2,*X;  
  
    count = 1 << r;               // 计算付立叶变换点数  
  
    // 分配运算所需存储器  
    W  = new complex<double>[count / 2];  
    X1 = new complex<double>[count];  
    X2 = new complex<double>[count];  
  
    // 计算加权系数  
    for(i = 0; i < count / 2; i++)  
    {  
        angle = -i * PI * 2 / count;  
        W[i] = complex<double> (cos(angle), sin(angle));  
    }  
  
    // 将时域点写入X1  
    memcpy(X1, TD, sizeof(complex<double>) * count);  
  
// 采用蝶形算法进行快速付立叶变换  
    for(k = 0; k < r; k++)//k为蝶形运算的级数  
    {  
        for(j = 0; j < 1 << k; j++)  
        {  
            bfsize = 1 << (r-k);//做蝶形运算两点间距离  
            for(i = 0; i < bfsize / 2; i++)   
            {  
                p = j * bfsize;  
                X2[i + p] = X1[i + p] + X1[i + p + bfsize / 2];  
                X2[i + p + bfsize / 2] = (X1[i + p] - X1[i + p + bfsize / 2])   
                    * W[i * (1<<k)];  
            }  
        }  
        X  = X1;  
        X1 = X2;  
        X2 = X;  
    }  
    // 重新排序  
    for(j = 0; j < count; j++)  
    {  
        p = 0;  
        for(i = 0; i < r; i++)  
        {  
            if (j&(1<<i))  
            {  
                p+=1<<(r-i-1);  
            }  
        }  
        FD[j]=X1[p];  
    }  
  
    delete W;  
    delete X1;  
    delete X2;   
}  

二维FFT

第三方库

效率