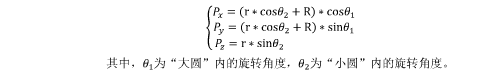Opengl绘制花托(一)
一..绘制花托的原理
花托也可以看做是一个轮胎形状。要绘制花托,就要了解花托形成的原理,从而计算出花托的各个坐标值。
也就像我们画圆一样,计算出圆的公式,从而可以画出来。要了解花托的形成原理,就必须选择一个通用
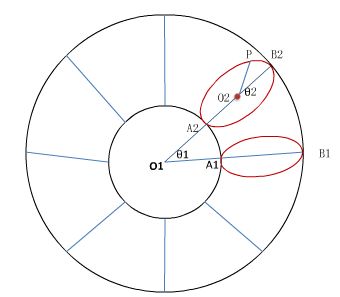
的横截面来分析。如下图花托的横截面所示,让红色部分的圆绕远点旋转360度就形成花托。
为了方便描述,我们规定:
圆心O1和O2的距离,我们称之为大半径,用R 表示,对应的圆称之为“大圆”;
以O2为圆心的圆的半径,我们称之为小半径,用r表示,对应的圆称之为小圆;
也就是说,“大圆”是我们正面看到的边界在花托中线的圆。“小圆”是我们侧面看到的一个截面。
从设计程序的角度来说,绘制这个花托需要两层循环:外循环负责旋转“大圆”内的角度值,内循环负责旋转
“小圆”的角度值。“大圆”每旋转一个角度步长值,“小圆”就要完成一圈的旋转。更进一步,我们在大圆上采集80
个点(实际上每个点都是一个“小圆”的圆心),在“小圆”上采集40个点。
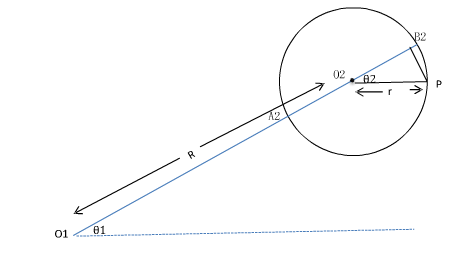
现在我们来考虑在“小圆”上采集的这些点的坐标,这里使用俯瞰图分析比较方便(实际上下图的上下方向
分别代表z轴的负正方向)至于圆截面x轴的选取,我们选择大圆半径方向的延长线所在的直线为x轴。这样选取
的好处在于,这条直线在xy平面上(关键就是这点),“小圆”边界上的点只能投影到这条直线上,再根据“大圆”
内的旋转角度,就可以计算出“小圆”边界上的点在世界坐标系中的x和y坐标,而“小圆”边界上的点离这条直线
的距离其实就是世界坐标系中z坐标值。
俯瞰图下的一个截面
由上面三维空间图,课的到“小圆”上的采样点的坐标: