巴切奇偶排序网络的原理分析
巴切奇偶排序网络的原理分析
分类: 算法与数据结构
2006-07-02 03:35
1267人阅读
评论(1)
收藏
举报
网络 算法 c
巴切奇偶排序网络的原理分析
排序网络是一种非常适合于硬件实现的排序方法。它使用的算法是一种非适应性排序。所谓非适应性排序,就是指它排序的每个步骤所涉及到的待排序元素的位置都是一定的,而不是像快速排序这样的适应性排序,根据不同的输入数据有不同的划分位置,从而涉及的元素的位置也不一样。
下面我们先根据简单的例子来说明排序网络是如何运作的:
例一:排序
DCBA
。排序的顺序如下
其中用粗线连接起来的是代表用交换器进行比较之后进行的交换动作。比如在第一段网络中,
C
、
B
相比较,因为
C>B
,所以
C
、
B
相交换。
四元巴切奇偶排序的原理是显而易见的,先是前两个元素排序,再是后两个元素排序,然后前一部分的最小值和后一部分的最小值排序,获得四个元素的最小值放在第一个位置;前一部分的最大值和后一部分的最大值排序,获得四个元素的最大值放在最后一个位置,最后在中间的两个元素进行排序。经过这一轮的排序后,得到了一个排好序的数组。
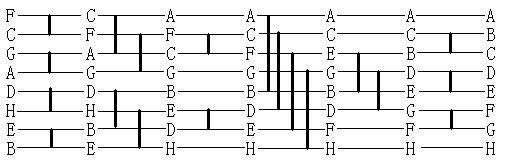
例二:排序
FCGADHEB
。
8
元的巴切奇偶排序,先进行前四个元素的排序,再进行后四个元素的排序,最后进行
8
个元素的排序。
根据上面的两个例子,我们可以看到,巴切奇偶排序的第一步首先是两两元素进行比较交换,小的移动到前面;然后就是四四进行排序,八八进行排序等等。
巴切奇偶排序的原理是怎样的呢?下面我们以
8
元巴切奇偶排序为例进行分析证明,看看巴切奇偶排序为什么能够以固定的数据处理顺序来排序任何的输入数据。
我们先来规定证明的语法约定:
1.
用
1 2 3 4 5 6 7 8
来表示上面例子的图中从上到下八个位置的数。
2.
用
max(1,2)
表示第一个位置的元素和第二个位置的元素中较大的一个;用
min(1,2)
表示第一个位置的元素和第二个位置的元素中较小的一个。
3.
max
(
min(1,2), max(3,4)
)表示在
min(1,2)
和
max(3,4)
中较大一个。
4.
因为四元排序的原理我们前面已经讲解过了,所以我们的证明开始于运用两次四元排序获得前后两个已经排序的四元组的状态开始,也就是例二图中的左数第四个状态:
ACFG BDEH
。这时数组的状态为:前四个元素有序,后四个元素也有序,而前后两组元素之间的关系未确定。我们用编号
1 2 3 4 5 6 7 8
来表示初始状态中从上到下的八个位置的元素。
5.
当表示“初始状态中第一个位置的元素比第二个位置的元素要小”,我们这样表示:
1<2
有了上面的证明语法约定,我们下面开始证明:
进行第一次交叉排序,即对于任意的
1<=i<=4
,对
a[i]
和
a[i+n/2]
进行比较交换操作,操作后的结果如下所示:(从上到下)
○
min(1,5)
○ min(2,6)
○ min(3,7)
○ min(4,8)
○ max(1,5)
○ max(2,6)
○ max(3,7)
○ max(4,8)
从上面这一步可以推出一个对后面有用的结论。先看看min(1,5)和min(2,6)的真值表:
|
Min(1,5)
|
Min(2,6)
|
条件
|
结论
|
|
1
|
2
|
1<5 && 2<6
|
min(1,5)<min(2,6)
|
|
1
|
6
|
1<5<6<2
|
min(1,5)<min(2,6)
|
|
5
|
2
|
5<1<2<6
|
min(1,5)<min(2,6)
|
|
5
|
6
|
5<1 && 6<2
|
min(1,5)<min(2,6)
|
真值表反映出一个结论,min(1,5)恒小于min(2,6),同理可以得出min(1,5)<min(2,6)<min(3,7)<min(4,8),max(1,5)<max(2,6)<max(3,7)<max(4,8)。
然后,进行第二次交叉排序,即进行当前的第三个位置(
min(3,7)
)与第五个位置(
max(1,5)
)以及第四个位置(
min(4,8)
)与第六个位置(
max(2,6)
)的比较交换,操作后的结果如下所示:
○ min(1,5)
第一组:
○ min(2,6)
○ min(min(3,7),max(1,5))
第二组:
○ min(min(4,8),max(2,6))
○max(min(3,7),max(1,5))
第三组:
○ max(min(4,8),max(2,6))
○ max(3,7)
○ max(4,8)
从例子中的最后一段的比较交换操作可以看出,是对上图标出的三组元素分别进行排序,最后就得出了一个排好序的数组。这个操作的前提是第一组的两个元素都比第二组的两个元素小,第二组的两个元素又都比第三组的两个元素小。
下面我们就来证明上面提出的这个前提条件:
要证明第一组的元素比第二组的元素小,只要证明第一组中的最大项比第二组的两个项都要小。
先假设min(2,6)>min(min(3,7),max(1,5)),即第一组最大项为min(2,6)。
下面证明它比min(min(4,8),max(2,6))要小。
因为从上一步的结论中可以知道min(2,6)<min(4,8),而min(2,6)<max(2,6),因此min(2,6)< min(min(4,8),max(2,6))。
然后证明min(2,6)比max(min(3,7),max(1,5))要小。
由假设条件min(2,6)>min(min(3,7),max(1,5)),可以推出:
min(2,6)>min(3,7)
或 min(2,6)>max(1,5)
因为min(2,6)>min(3,7)不成立,所以
min(min(3,7),max(1,5))=max(1,5)
max(min(3,7),max(1,5))=min(3,7)
而由于min(2,6)<min(3,7),所以min(2,6)< max(min(3,7),max(1,5))得证。
然后假设min(2,6)<min(min(3,7),max(1,5)),那么第一组的最大项就为min(min(3,7),max(1,5)),我们现在要证明它比第二组的两个元素都小。
先证明min(min(3,7),max(1,5))< min(min(4,8),max(2,6))。
这里分为两种情况:
i)
min(3,7)<max(1,5)
,min(min(3,7),max(1,5))=min(3,7)
要证明min(3,7)小于第二组的两个项。
先证明min(3,7)<min(min(4,8),max(2,6))
如果min(4,8)<max(2,6),则由min(3,7)<min(4,8),得证。
如果min(4,8)>max(2,6),则由假设min(3,7)<max(1,5),再根据max(1,5)<max(2,6),有min(3,7)<max(2,6),得证。
然后,min(min(3,7),max(1,5))小于max(min(3,7),max(1,5)),不需要证明。
ii)
min(3,7)>max(1,5)
,min(min(3,7),max(1,5))=max(1,5)
要证明max(1,5)小于第二组的两个项。
同上一种情况,只需要证明max(1,5)< min(min(4,8),max(2,6))
如果min(4,8)<max(2,6),则由假设max(1,5)<min(3,7),再根据min(3,7)<min(4,8),有max(1,5)<min(4,8),由此得证。
如果min(4,8)>max(2,6),则由max(1,5)<max(2,6),直接得证。
由上面的证明,我们可以得出一个结论,第一组两个元素小于第二组两个元素。同理可证,第二组的两个元素小于第三组的两个元素。因此,只要三组中的两个元素分别排好序,因为数组中的最小值和最大值都放到了正确的位置,所以整个数组就是有序的了。