图说线段树和树状数组
PS:直接看黑体字和图片吧
线段树(segment tree)
从一个问题说起吧,(HDOJ1166)
给定一个数列A1,A2......,An (n<50000) 以及一堆操作(可多达40000个操作),按顺序执行这些操作。
+ Add i k 操作:Ai += k
+ Sub i K操作:Ai -= k
+ Query i j 操作:输出Ai到Aj的和 sum=Ai+....+Aj
很显然这个问题只要用一个数组储存数列A1,A2......,An然后按要求执行操作就可以解决,Add i k就让A[i]加上k,
Sub i k就让A[i]减去k,Query i j 就用一个for循环从Ai加到Aj得出和输出即可。不过这样做效率有点低,那么怎样才能提
高效率呢?很明显我们发现这里最花时间的操作是Query,假如有很多Query 1 n操做,我们每完成一次Query操作都需
要遍历一遍数组以求出A1到An的和,这是很耗费时间的,怎样才能加快Query 1 n操作的速度呢,一个很基本的想法是
空间换时间,用一个变量S保存A[1]到A[n]的和,在Add和Sub操作的时候我们除了对A[i]进行操作外顺便也维护S的值,
在遇到Query 1 n时我们便不用遍历数组直接输出S的值即可。Query 1 n这个特定操作的效率是提上来了,不过在所有
的操作中还有很多其他的Query 比如Query 10 500, Query 200 1000.....,为满足一般性的Query,我们可用一棵二叉树
递归地保存1...n的和1...n/2,n/2...n的和...
S[1...n]
S[1...n/2] S[n/2...n]
S[1...n/4] S[n/4...n/2] S[n/2...3n/4] S[3n/4...n]
.......
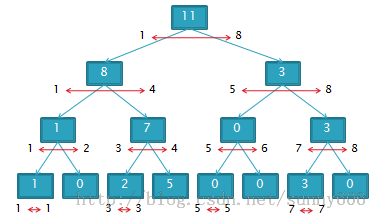
如图:(Figure1)
Add i k 操作:(Figure2)
Query 操作:(Figure3)
这样Add,Sub,Query操作都能在log(n)的时间完成。这个东西就是传说中的线段树。
void update(int rt,int l,int r,int p,int key)
{
if(l == r)
{
tree[rt]+=key;
return ;
}
int mid = (l+r)>>1;
if(p<=mid) update(rt<<1,l,mid,p,key);
else update((rt<<1)|1,mid+1,r,p,key);
tree[rt] = tree[rt<<1]+tree[(rt<<1)|1];
}
int query(int rt,int l,int r,int s,int e)
{
if(l==s && r==e) return tree[rt];
int mid = (l+r)>>1;
if(e<=mid) return query(rt<<1,l,mid,s,e);
if(s>mid) return query((rt<<1)|1,mid+1,r,s,e);
return query(rt<<1,l,mid,s,mid)+query((rt<<1)|1,mid+1,r,mid+1,e);
}
树状数组(binary indexed tree)
在一些实际应用中我们只关心一个数列的前缀和,即只所有的Query都是Query 1 i这种特定类型的Query
给定一个数列A1,A2......,An 以及一堆操作,按顺序执行这些操作。
+ Add i k 操作:Ai += k
+ Sub i K 操作:Ai -= k
+ Query i 操作:输出Ai到Aj的和 sum(i)=A1+....+Ai
用上面所介绍的线段树显然是可以解决这个问题的,而且我们发现由于我们发现二 叉树所有的右孩子去掉后我们仍能
够求出所有的A1+......+Ai,对于一颗有n个叶节点的完全二叉树T,T共有2n-1个节点,右孩子一共是n-1个,去掉这些
右孩子节点后T刚好是n个节点,
Figure4
给每个节点编号就成了下面的样子,观察发现,sum(8)=T[8]用二进制表示即sum(1000)=T[1000]
sum(6)=T[4]+T[6],用二进制表示为sum(0110)=T[0100]+T[0110],看出规律了吧。看下图发现
把Binary indexed tree翻译为树状数组是翻译得很贴切的。
Figure5
POJ3468 -- A Simple Problem with Integers(成段更新)
+add i j k 对Ai到Aj的所有元素加上k
+query i j 输出Ai到Aj的和
对于add i j k操做我们可以用一个for循环对一个段i,j的所有元素按上面的update函数逐个进行更新,不过
这样add操作就成nlogn的了,想一下之前是怎样加速Query操作的,要加快成段操作的速度的关键是尽量
用一个节点记录下一个段的数据,所以我们可以给每个节点增加一个域用来记录成段的增量。
POJ3468 (如何用树状数组完成成段更新)
计算sum(i)=A1+.......+Ai
如果给区间[l,r)成段更新加上k,
nsum(i)= sum(i) i<l
nsum(i)=sum(i) + x*i - x(l-1)
nsum(i)=sum(i) + x(r-l+1)
所以我们可以用两个树状数组bit1,bit2来记录,sum(i)=sum(bit2,i)*i (注意乘i)+ sum(bit1,i)
update(l,r,k){
add(bit1, l , -k*l-1);
add(bit1, r+1, k*r);
add(bit2, l, k);
add(bit2, r+1, -k);
}
其实sum(i)可以看成一个积分的过程,
如果对上面四个add的意义有点晕就看看下面的图吧,冲击函数H[i]的积分就是阶跃函数A[i](成段增量),
add(bit2,l,k),add(bit2,r+1,-k)记录的就相当于冲击函数,再联想到sum(i)=sum(bit2,i)*i (注意乘i)+ sum(bit1,i),
A[i]的积分就是sum[i]。
Figure6