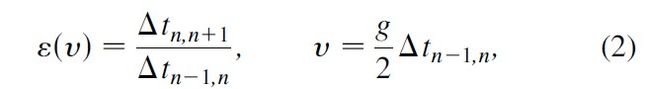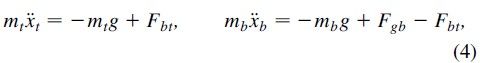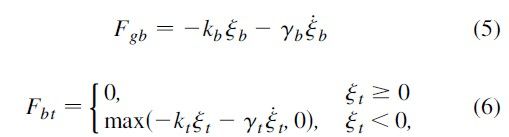Complex Velocity Dependence of the Coefficient of Restitution of a Bouncing Ball札记
Müller P, Heckel M, Sack A, et al. Complex Velocity Dependence of the Coefficient of Restitution of a Bouncing Ball[J]. Physical Review Letters, 2013, 110(25): 254301.
1. 简介
本文发表在物理学顶级杂志PRL上,主要解决COR(The coefficient of normal restitution)的问题,文章指出在小球碰撞过程中,COR可以表示为碰撞速度的函数,而通过实验得知的结果推知,当前的COR衰变过程需要补充一个振荡函数,这个现象至今无人发现是因为统计离散(statistical scatter)导致的。而作者通过大量自动实验得出了上述结果。
2. COR
COR具体解释可以查看维基:http://en.wikipedia.org/wiki/Coefficient_of_restitution
在碰撞过程中,碰撞前后的速度有如下关系,如公式(1),左侧表示碰撞前的速度,右侧表示之后的速度:
根据(1)式可以获得 ε(v) 的表达式。
通过能量守恒定律,可一得到 v 的表达式,将其表示为 高度 h 的函数,进而得到 ε(v) 的表达式,如公式(3)所示:
同理,将速度表示为 碰撞时间差 △t 的函数即得到,公式(2):
最终的 ε(v) 即可按照如上公式进行计算,而后作者进行了实验。
3. bouncing ball experiments
作者使用直径6mm的不锈钢小球 和 一个相对巨大的玻璃板面积 40×20×2 cm² 及 一个水平的钢制底板 重 8kg。
小球会在初始高度H0( 8 ~ 12 cm)处释放,小球大概经过80~100次碰撞后停止,通过公式(2)可以获得ε(v)的参数,时间可以由底板上的电子传感器获得。
4. 碰撞模型
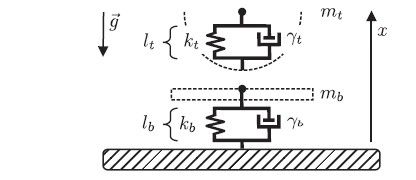
下表t表示top顶点,b表示bottom低点,其中γ可以理解为粘滞参数,而 x 为所处高度,x'表示 速度,x'' 表示加速度。将小球可以想象成一个类似弹簧的质点。根据牛顿第二定律进行受力分析可得,
其中 Fbt 与 Fgb有如下方式获得,物理意义也很清楚,由受力分析即可得出结果,
从而由上式中解微分方程组即可获得相应的解进而求的COR.
初始高度为H01, 我们利用上式可以解得H12, H23等,进而利用公式(3)获得 ε2.
5. MATLAB 仿真代码
BallImpact.m
clear all
%
rt = 0;%0.025;%damping
rb = 0;%0.09;%rt=0;%rb=0;
mb = 1/1000;%mass /kg
mt = 1/1000;
kb = 500;%sping constant
kt = 500;
lb = 1/1000;%spring length /m
lt = 1/1000;
g = 9.81;% gravitational acceleration
xb0 = lb - mb*g/kb;
h01array= 0.0001:0.0001:0.018;
t12array = zeros(1,length(h01array));
t23array = zeros(1,length(h01array));
h12array = zeros(1,length(h01array));
h23array = zeros(1,length(h01array));
for i=1:length(h01array)
i,
h01=h01array(i);
xt0 = xb0 + lt + h01;
%
%%%%求解常微分方程组,获得Y(1) Y(3)为Xt Xb的运动轨迹
[T,Y] = ode15s('BallModel',[0 0.5],[xt0 0 xb0 0]);
xt=Y(:,1);vt=Y(:,2);xb=Y(:,3);vb=Y(:,4);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
[pks1,locs1] = findpeaks(-xt);%xt-xb的极小值可以理解为碰撞发生的时刻公式2
[pks2,locs2] = findpeaks(xt);
t1=T(locs1(1));t2=T(locs1(2));h12 = pks2(1);
if xt(locs2(2))-xt(locs1(2))<0.2*( xt(locs2(1))-xt(locs1(1)))
t3=T(locs1(4));h23=pks2(3);
else t3=T(locs1(3));h23=pks2(2);
end
t12 =t2-t1;
t23 = t3-t2;
h12array(i)=h12;h23array(i)=h23;
t12array(i)=t12;t23array(i)=t23;
end
v2= sqrt(2*g*h12array);
E2= sqrt(h23array./h12array);
E23 = t23array./t12array;
v23 = g*t12array/2;
figure
[v2,index]=sort(v2);E2=E2(index);h01arrayt=h01array(index);
%[v23,index]=sort(v23);E23=E23(index);h01arrayh=h01array(index);
plot(v2,E2,'-b.');%此图即Fig3(a)即Fig4 with rb&rt
%axis([0.2 0.61 0 1.1]);
%hold on
%plot(v23,E23,'-r.');
BallModel.m
%此段代码主要描述方程(4)(5)(6)
function dy = BallModel(t,y)
%
rt = 0;%0.025;%damping
rb = 0;%0.09;
%rt=0;
%rb=0;
mb = 1/1000;%mass /kg
mt = 1/1000;
kb = 500;%sping constant
kt = 500;
lb = 1/1000;%spring length /m
lt = 1/1000;
g = 9.81;% gravitational acceleration
%
xt=y(1);vt=y(2);xb=y(3);vb=y(4);
dy = zeros(4,1);
dy(1) = vt;
dy(3) = vb;
xit=xt-xb-lt;
if xit>=0
Fbt = 0;
else
Fbt =max(-kt*xit-rt*vt,0);
end
dy(2) = -g + Fbt/mt;
dy(4) = -g +(-kb*(xb-lb)-rb*vb)/mb-Fbt/mb;
end
FIG 3.
FIG.4.