图像处理基本算法 Hough变换
霍夫变换是图像处理中从图像中识别几何形状的基本方法之一,应用很广泛,也有很多改 进算法。最基本的霍夫变换是从黑白图像中检测直线(线段)。广义的Hough变换已经不仅仅局限于提取直线,二值任意可以用表达式表达的曲线,比如圆,椭圆,正弦余弦曲线,等等,但是曲线越是复杂,所需参数越多,运算的时间也就越多。归根结底,Hough变换的精髓在于投票机理,将图像空间转换到参数空间进行求解。我们先看这样一个问题:设已知一黑白图像上画了一条直线,要求出这条直线所在的位置 。我们知道,直线的方程可以用y=k*x+b 来表示,其中k和b是参数,分别是斜率和截距。过某一点 (x0,y0)的所有直线的参数都会满足方程y0=kx0+b。即点(x0,y0)确定了一族直线。方程y0=kx0+b在 参数k–b平面上是一条直线,(你也可以是方程b=-x0*k+y0对应的直线)。这样,图像x–y平面上的 一个前景像素点就对应到参数平面上的一条直线。我们举个例子说明解决前面那个问题的原理。设 图像上的直线是y=x, 我们先取上面的三个点:A(0,0), B(1,1), C(22)。可以求出,过A点的直线 的参数要满足方程b=0, 过B点的直线的参数要满足方程1=k+b, 过C点的直线的参数要满足方程 2=2k+b, 这三个方程就对应着参数平面上的三条直线,而这三条直线会相交于一点(k=1,b=0)。 同 理,原图像上直线y=x上的其它点(如(3,3),(4,4)等) 对应参数平面上的直线也会通过点(k=1,b=0) 。这个性质就为我们解决问题提供了方法:首先,我们初始化一块缓冲区,对应于参数平面,将其所有数据置为0.对于图像上每一前景点,求出参数平面对应的直线,把这直线上的所有点的值都加1。最后,找到参数平面上最大点的位置,这个位置就是原图像上直线的参数。上面就是霍夫变换的基本思想。就是把图像平面上的点对应到参数平面上的线,最后通过 统计特性来解决问题。假如图像平面上有两条直线,那么最终在参数平面上就会看到两个峰值点, 依此类推。在实际应用中,y=k*x+b形式的直线方程没有办法表示x=c形式的直线(这时候,直线的斜 率为无穷大)。所以实际应用中,是采用参数方程p=x*cos(theta)+y*sin(theta)。这样,图像平面 上的一个点就对应到参数p—theta平面上的一条曲线上。其它的还是一样。Hough变换求取直线的源码:
Hough变换求取直线的源码:
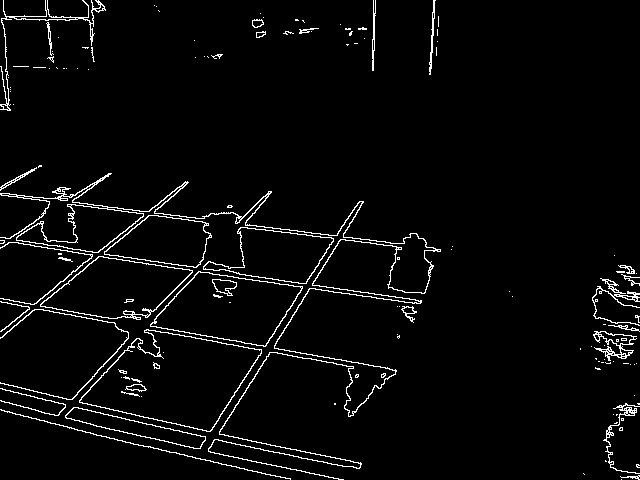
//提取直线 能够在二值图像中提取场地中的白线,并进行重建
//采用Hough变换
#include <iostream>
#include<cv.h>
#include <highgui.h>
#include <math.h>
#define PI 3.1415926
using namespace std;
int main(){
IplImage * image,*image2;
image = cvLoadImage("E:\\image\\game\\board.bmp",0);
cvNamedWindow("image",1);
cvShowImage("image",image);
//Hough变换
//用Hough提取出所有的直线,并在一张新图中进行绘制
image2 = cvCreateImage(cvSize(image->width,image->height),image->depth,1);
int i,j;
unsigned char *ptr,* dst;
//参数空间的参数 角度0~度 每格2度 distance = fabs(x*cosA + y *sinA)
double angle;
int distance;
int PerAngle = 2;
int m,n;
int AngleNum = 90; //角度范围0~360度
int maxDistance = (int)(sqrt(pow((double)image->width,2)+ pow((double)image->height,2)) + 2 );
//cout<<maxDistance<<endl;
//参数空间各个点的统计值,使用一维数组,排序方便
//申请一块内存,存放各个直线的出现次数
int * number = new int [AngleNum * maxDistance];
double Hsin,Hcot;
int count = 0;
int max ,lineAngle, rol;
//number赋值0
for (i= 0; i< AngleNum * maxDistance; i++)
{
number[i] = 0;
}
for (i = 0 ; i< image->height; i++)
{
for (j = 0 ; j < image->width ; j++)
{
ptr = (unsigned char *)image->imageData + i*image->widthStep +j;
//统计每个直线出现的概率
if ( *ptr != 0)
{
//count++;
//cout<<count<<endl;
for (m = 0 ; m < AngleNum; m++ )
{
angle = (double)m*PerAngle*PI/180.0;
distance = (int)(fabs(j*cos(angle)+ i*sin(angle)));
//cout<<"distance: "<< distance<<endl;
//*(number+ AngleNum* (int)(distance + 0.5) + m) = (*(number+ AngleNum* (int)(distance + 0.5) + m)) +1;
number[AngleNum * distance + m]++;
}
}
}
}
//打印各个方格的统计个数
for (m = 0 ; m <maxDistance; m++)
{
for (n = 0 ; n < AngleNum; n++ )
{
if (number[AngleNum * m + n] > 100)
{
printf("angle %d distance : %d number %d\n",n*2 , m , number[AngleNum* m + n] );
}
}
}
//首先将image2 的所有值赋值为0
for (i = 0 ; i< image2->height; i++)
{
for (j = 0 ; j< image2->width; j++)
{
dst =(unsigned char *) image2->imageData + i*image->widthStep + j;
*dst =0;
}
}
//寻找变换域中的直线 假设一条直线上有20个点以上,则认为是一条直线 那么就在新的图片中画出该直线
//寻找概率最大的直线
/* 添加直线
lineAngle = 0;
rol = 0;
max = number[0];
for (m = 0 ;m< maxDistance ;m++ )
{
for (n = 0 ; n< AngleNum; n++)
{
if (number[AngleNum * m + n] > max)
{
max =number[AngleNum * m + n];
rol = m;
lineAngle = n;
}
}
}
cout<<"m :" <<rol<<" n:"<<lineAngle<<" max" << max<<endl;
//根据角度和距离在image2中添加该图片
angle = lineAngle*PerAngle*PI/180;
Hcot = cos(angle)/sin(angle);
Hsin = sin(angle);
for (j = 0;j< image2->width;j++ )
{
i = (int)(rol/Hsin - j*Hcot);
dst = (unsigned char*)image2->imageData + i*image->widthStep + j;
*dst = 255;
}
//添加第二条直线
//最大值邻域处赋值为0
number[rol*AngleNum+ lineAngle] = 0;
for (m = rol-1 ; m<= rol+1; m++)
{
for (n = lineAngle -1 ; n<= lineAngle +1 ; n++)
{
number[m*AngleNum + n] = 0;
}
}
max = number[0];
lineAngle = 0;
rol = 0;
for (m = 0 ;m < maxDistance ;m++ )
{
for (n = 0 ; n < AngleNum; n++)
{
if (number[AngleNum * m + n] > max)
{
max =number[AngleNum * m + n];
rol = m;
lineAngle = n;
}
}
}
cout<<"m :" <<rol<<" n:"<<lineAngle<<" max" << max<<endl;
//根据角度和距离在image2中添加该图片
angle = lineAngle*PerAngle*PI/180;
Hcot = cos(angle)/sin(angle);
Hsin = sin(angle);
for (j = 0;j< image2->width;j++ )
{
i = (int)(rol/Hsin - j*Hcot);
if (i< 0 ){i = 0;}
if(i>= image2->height){i = image2->height -1;}
dst = (unsigned char*)image2->imageData + i*image->widthStep + j;
*dst = 255;
}
*/
//画出所有可能的直线
for (m = 0 ;m< maxDistance ; m++)
{
for (n = 0 ; n< AngleNum ;n++)
{
if (number[m*AngleNum + n] > 110)
{
rol = m;
lineAngle = n;
//根据角度和距离在image2中添加该图片
angle = lineAngle*PerAngle*PI/180;
Hcot = cos(angle)/sin(angle);
Hsin = sin(angle);
for (j = 0;j< image2->width;j++ )
{
i = (int)(rol/Hsin - j*Hcot);
if (i< 0 ){i = 0;}
if(i>= image2->height){i = image2->height -1;}
dst = (unsigned char*)image2->imageData + i*image->widthStep + j;
*dst = 255;
}
}
}
}
cvNamedWindow("image2",1);
cvShowImage("image2",image2);
//cvSaveImage("E:\\image\\game\\changjian.bmp",image2);
delete [] number;
cvWaitKey(0);
return 0;
}
在看下面一个问题:我们要从一副图像中检测出半径以知的圆形来。这个问题比前一个还 要直观。我们可以取和图像平面一样的参数平面,以图像上每一个前景点为圆心,以已知的半径在 参数平面上画圆,并把结果进行累加。最后找出参数平面上的峰值点,这个位置就对应了图像上的 圆心。在这个问题里,图像平面上的每一点对应到参数平面上的一个圆。
把上面的问题改一下,假如我们不知道半径的值,而要找出图像上的圆来。这样,一个办 法是把参数平面扩大称为三维空间。就是说,参数空间变为x–y–R三维,对应圆的圆心和半径。 图像平面上的每一点就对应于参数空间中每个半径下的一个圆,这实际上是一个圆锥。最后当然还 是找参数空间中的峰值点。不过,这个方法显然需要大量的内存,运行速度也会是很大问题。
有什么更好的方法么?我们前面假定的图像都是黑白图像(2值图像),实际上这些2值图像 多是彩色或灰度图像通过边缘提取来的。我们前面提到过,图像边缘除了位置信息,还有方向信息 也很重要,这里就用上了。根据圆的性质,圆的半径一定在垂直于圆的切线的直线上,也就是说, 在圆上任意一点的法线上。这样,解决上面的问题,我们仍采用2维的参数空间,对于图像上的每 一前景点,加上它的方向信息,都可以确定出一条直线,圆的圆心就在这条直线上。这样一来,问 题就会简单了许多。
Hougu变换求取圆源码:
/************************************************************************/
/* Hough圆变换 */
/************************************************************************/
//白纸上的黑圆圈
#include<cv.h>
#include <highgui.h>
#include <math.h>
#include <iostream>
using namespace std;
int main(){
IplImage * image, *image2;
image = cvLoadImage("E:\\image\\circle2.bmp",0);
cvNamedWindow("image",1);
cvShowImage("image",image);
image2 = cvCreateImage(cvSize(image->width,image->height),image->depth,1);
int i ,j;
int temp = 0;
unsigned char *ptr, *dst;
//参数空间的参数 圆心O(a,b) 半径radius
int a = 0,b = 0,radius = 0;
//累加器
int A0 = image->height;
int B0 = image->width;
int R0 = (image->width > image->height)? 2*image->width : 2*image->height;//R0取长宽的最大值的2倍
int countLength = A0*B0*R0;
int * count = new int[countLength];
//偏移
int index = A0 * B0 *radius + A0*b + a;
//为累加器赋值0
for (i= 0;i<countLength;i++)
{
count[i]=0;
}
//printf("%d",R0);
for (i = 0 ; i< image->height; i++)
{
for (j = 0 ; j< image->width ; j++)
{
ptr = (unsigned char *)image->imageData + i*image->widthStep + j;
//检测黑线
if (*ptr == 0 )
{
//遍历a ,b 为;累加器赋值
for (a = 0 ; a< A0;a++)
{
for (b = 0; b< B0;b++)
{
radius = (int)(sqrt(pow((double)(i-a),2) + pow((double)(j - b),2)));
index = A0 * B0 *radius + A0*b + a;
count[index]++;
temp = count[index];
// printf("%d\n",count[index]);
}
}
}
}
printf("%d\n",i);
}
//image2全部赋值为0
for (i= 0; i<image2->height; i++)
{
for (j = 0 ; j< image2->width;j++)
{
dst = (unsigned char *)image2->imageData + i*image2->widthStep + j;
*dst = 0;
}
}
//遍历累加器数组,找出所有的圆
for (a = 0 ; a < A0 ; a++)
{
for (b = 0 ; b< B0; b++)
{
for (radius = 0 ; radius < R0; radius++)
{
index = A0 * B0 *radius + A0*b + a;
if (count[index] > 100)
{
printf("a: %d b: %d r: %d num: %d\n",a,b,radius,count[index]);
//在image2中绘制该圆
for (j = 0 ; j< image->width;j++)
{
i = (int)(sqrt(pow((double)radius,2)- pow((double)(j-b),2)) + a);
if ((i< image2->height) && (i >= 0))
{
dst = (unsigned char*)(image2->imageData + i * image2->widthStep + j);
*dst = 255;
}
//i有两个值
i = a -(int)(sqrt(pow((double)radius,2)- pow((double)(j-b),2)));
if ((i< image2->height) && (i >= 0))
{
dst = (unsigned char*)(image2->imageData + i * image2->widthStep + j);
*dst = 255;
}
}
}
}
}
}
cvNamedWindow("image2",1);
cvShowImage("image2",image2);
cvSaveImage("E:\\image\\circleHough2.bmp",image2);
cvWaitKey(0);
return 0 ;
}
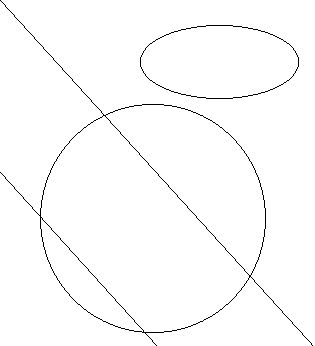
接下来还有许多类似的问题,如检测出椭圆,正方形,长方形,圆弧等等。这些方法大都 类似,关键就是需要熟悉这些几何形状的数学性质。霍夫变换的应用是很广泛的,比如我们要做一 个支票识别的任务,假设支票上肯定有一个红颜色的方形印章,我们可以通过霍夫变换来对这个印 章进行快速定位,在配合其它手段进行其它处理。霍夫变换由于不受图像旋转的影响,所以很容易 的可以用来进行定位。
霍夫变换有许多改进方法,一个比较重要的概念是广义霍夫变换,它是针对所有曲线的, 用处也很大。就是针对直线的霍夫变换也有很多改进算法,比如前面的方法我们没有考虑图像上的 这一直线上的点是否连续的问题,这些都要随着应用的不同而有优化的方法。
顺便说一句,搞图像处理这一行,在理论方面,有几本杂志是要看的,自然是英文杂志, 中文期刊好象没有专门的图像处理期刊,当然也有不少涉及这方面的期刊,但事实求是来说,的确 比英文杂志水平差很多。
‘IEEE Transactions on Pattern And Machine Intelligence’
‘IEEE Transactions on Image Processing’
是最重要的两本,其它的如ICIP等的会议文章也非常好。不过,要不想很偏理论, 这些玩艺儿也没什么要看的。
2.简单点概括就是:Hough变换的基本原理在于利用点与线的对偶性,将原始图像空间的给定的曲线通过曲线表达形式变为参数空间的一个点。这样就把原始图像中给定曲线的检测问题转化为寻找参数空间中的峰值问题。也即把检测整体特性转化为检测局部特性。比如直线、椭圆、圆、弧线等。
算法如下:
(1)初始化一个变换域空间的数组,r方向上的量化数目图像对角线方向像素,O方向上的量化数目为180。
(2)顺序搜索图像的所有黑点。对每一个黑点,在变换域的对应个点加一。
(3)求出变换域最大值点并记录。最大值点就是直线的所在了。
或者说:hough变换利用图像空间和hough参数空间的点-线对偶性,把图像空间中的检测问题转换到参数空间。通过在参数空间里进行简单的累加统计,然后在hough参数空间寻找累加器峰值的方法检测直线。例如,图1(a)中的九条线段对应于如图1(b)所示的其hough参数空间的九个累加器峰值。图1(b)中,hough参数空间的横纵坐标分别为直线极坐标方程:ρ=x×cos(θ) + y×sin(θ) 的两个参数ρ和θ。九个峰值的ρ和θ值唯一的确定其对应线段所在直线的两个参数。并且线段的长度决定坐标(ρ,θ)处的累加值的大小。