【字典树】串集合查找

Trie 树，又称字典树，单词查找树。它来源于retrieval(检索)中取中间四个字符构成(读音同try)。用于存储大量的字符串以便支持快速模式匹配。主要应用在信息检索领域。

Trie 有三种结构： 标准trie (standard trie)、压缩trie、后缀trie(suffix trie) 。 最后一种将在后缀树（点击打开链接）中详细讲，这里只将前两种。

1. 标准Trie (standard trie)

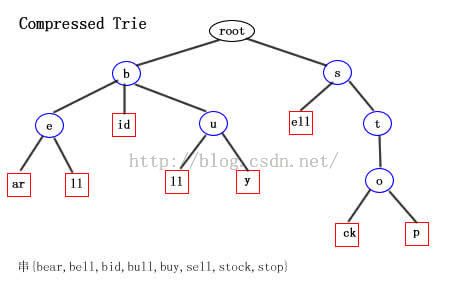
标准 Trie树的结构 ： 所有含有公共前缀的字符串将挂在树中同一个结点下。实际上trie简明的存储了存在于串集合中的所有公共前缀。 假如有这样一个字符串集合X{bear,bell,bid,bull,buy,sell,stock,stop}。它的标准Trie树如下图：

上图（蓝色圆形结点为内部结点，红色方形结点为外部结点），我们可以很清楚的看到字符串集合X构造的Trie树结构。其中从根结点到红色方框叶子节点所经历的所有字符组成的串就是字符串集合X中的一个串。

注意这里有一个问题：如果X集合中有一个串是另一个串的前缀呢？比如，X集合中加入串bi。那么上图的Trie树在绿色箭头所指的内部结点i 就应该也标记成红色方形结点。这样话，一棵树的枝干上将出现两个连续的叶子结点(这是不合常理的)。

也就是说字符串集合X中不存在一个串是另外一个串的前缀。如何满足这个要求呢？我们可以在X中的每个串后面加入一个特殊字符$(这个字符将不会出现在字母表中)。这样，集合X{bear$、bell$、.... bi$、bid$}一定会满足这个要求。

总结：一个存储长度为n，来自大小为d的字母表中s个串的集合X的标准trie具有性质如下：

(1) 树中每个内部结点至多有d个子结点。

(2) 树有s个外部结点。

(3) 树的高度等于X中最长串的长度。

(4) 树中的结点数为O(n)。

标准 Trie树的查找

对于英文单词的查找，我们完全可以在内部结点中建立26个元素组成的指针数组。如果要查找a，只需要在内部节点的指针数组中找第0个指针即可(b=第1个指针，随机定位)。时间复杂度为O(1)。

查找过程：假如我们要在上面那棵Trie中查找字符串bull (b-u-l-l)。

(1) 在root结点中查找第('b'-'a'=1)号孩子指针，发现该指针不为空，则定位到第1号孩子结点处——b结点。

(2) 在b结点中查找第('u'-'a'=20)号孩子指针，发现该指针不为空，则定位到第20号孩子结点处——u结点。

(3) ... 一直查找到叶子结点出现特殊字符'$'位置，表示找到了bull字符串

如果在查找过程中终止于内部结点，则表示没有找到待查找字符串。

效率：对于有n个英文字母的串来说，在内部结点中定位指针所需要花费O(d)时间，d为字母表的大小，英文为26。由于在上面的算法中内部结点指针定位使用了数组随机存储方式，因此时间复杂度降为了O(1)。但是如果是中文字，下面在实际应用中会提到。因此我们在这里还是用O(d)。查找成功的时候恰好走了一条从根结点到叶子结点的路径。因此时间复杂度为O(d*n)。

但是，当查找集合X中所有字符串两两都不共享前缀时，trie中出现最坏情况。除根之外，所有内部结点都自由一个子结点。此时的查找时间复杂度蜕化为O(d*(n^2))

标准 Trie树的Java代码实现：

package net.hr.algorithm.stroper;

import java.util.ArrayList;

enum NodeKind{LN,BN};
/**
 * Trie结点
 */
class TrieNode{

	char key;
	TrieNode[] points=null;
	NodeKind kind=null;
}
/**
 * Trie叶子结点
 */
class LeafNode extends TrieNode{
	
	LeafNode(char k){
		super.key=k;
		super.kind=NodeKind.LN;
	}
}
/**
 * Trie内部结点
 */
class BranchNode extends TrieNode{
	
	BranchNode(char k){
		super.key=k;
		super.kind=NodeKind.BN;
		super.points=new TrieNode[27];
	}
}
/**
 * Trie树
 * @author heartraid
 */
public class StandardTrie {

	private TrieNode root=new BranchNode(' ');
	
	/**
	 * 想Tire中插入字符串
	 */
	public void insert(String word){
		
		//System.out.println("插入字符串："+word);
		//从根结点出发
		TrieNode curNode=root;
		//为了满足字符串集合X中不存在一个串是另外一个串的前缀 
		word=word+"$";
		//获取每个字符
		char[] chars=word.toCharArray();
		//插入
		for(int i=0;i<chars.length;i++){
			//System.out.println("   插入"+chars[i]);	
			if(chars[i]=='$'){
				curNode.points[26]=new LeafNode('$');
			//	System.out.println("   插入完毕,使当前结点"+curNode.key+"的第26孩子指针指向字符：$");
			}
			else{
				int pSize=chars[i]-'a';
				if(curNode.points[pSize]==null){
					curNode.points[pSize]=new BranchNode(chars[i]);
				//	System.out.println("   使当前结点"+curNode.key+"的第"+pSize+"孩子指针指向字符: "+chars[i]);
					curNode=curNode.points[pSize];
				}
				else{
				//	System.out.println("   不插入，找到当前结点"+curNode.key+"的第"+pSize+"孩子指针已经指向字符: "+chars[i]);
					curNode=curNode.points[pSize];
				}
			}
		}
	}
	/**
	 * Trie的字符串全字匹配
	 */
	public boolean fullMatch(String word){
		//System.out.print("查找字符串："+word+"\n查找路径：");
		//从根结点出发
		TrieNode curNode=root;
		//获取每个字符
		char[] chars=word.toCharArray();
		
		for(int i=0;i<chars.length;i++){
			if(curNode.key=='$'){
				System.out.println('&');
			//	System.out.println(" 【成功】");
				return true;
			}else{
				System.out.print(chars[i]+" -> ");	
				int pSize=chars[i]-'a';
				if(curNode.points[pSize]==null){
				//	System.out.println(" 【失败】");
					return false;
				}else{
					curNode=curNode.points[pSize];
				}
			}
		}
	//	System.out.println("  【失败】");
		return false;
	}
	

	/**
	 * 先根遍历Tire树
	 */
	private void preRootTraverse(TrieNode curNode){
		
		if(curNode!=null){
			System.out.print(curNode.key+" ");
			if(curNode.kind==NodeKind.BN)
				for(TrieNode childNode:curNode.points)
					preRootTraverse(childNode);
		}
		
	}
	/**
	 * 得到Trie根结点
	 */
	public TrieNode getRoot(){
		return this.root;
	}
	/**
	 * 测试
	 */
	public static void main(String[] args) {
		
		StandardTrie trie=new StandardTrie();
		trie.insert("bear");
		trie.insert("bell");
		trie.insert("bid");
		trie.insert("bull");
		trie.insert("buy");
		trie.insert("sell");
		trie.insert("stock");
		trie.insert("stop");
		
		trie.preRootTraverse(trie.getRoot());
		
		trie.fullMatch("stoops");
	}
}

中文词语的标准Trie树

由于中文的字远比英文的26个字母多的多。因此对于trie树的内部结点，不可能用一个26的数组来存储指针。如果每个结点都开辟几万个中国字的指针空间。估计内存要爆了，就连磁盘也消耗很大。

一般我们采取这样种措施：

(1) 以词语中相同的第一个字为根组成一棵树。这样的话，一个中文词汇的集合就可以构成一片Trie森林。这篇森林都存储在磁盘上。森林的root中的字和root所在磁盘的位置都记录在一张以Unicode码值排序的有序字表中。字表可以存放在内存里。

(2) 内部结点的指针用可变长数组存储。

特点：由于中文词语很少操作4个字的，因此Trie树的高度不长。查找的时间主要耗费在内部结点指针的查找。因此将这项指向字的指针按照字的Unicode码值排序，然后加载进内存以后通过二分查找能够提高效率。

标准Trie树的应用和优缺点

(1) 全字匹配：确定待查字串是否与集合的一个单词完全匹配。如上代码fullMatch()。

(2) 前缀匹配：查找集合中与以s为前缀的所有串。

注意：Trie树的结构并不适合用来查找子串。这一点和前面提到的PAT Tree以及后面专门要提到的Suffix Tree的作用有很大不同。

优点： 查找效率比与集合中的每一个字符串做匹配的效率要高很多。在o(m)时间内搜索一个长度为m的字符串s是否在字典里。

缺点：标准Trie的空间利用率不高，可能存在大量结点中只有一个子结点，这样的结点绝对是一种浪费。正是这个原因，才迅速推动了下面所讲的压缩trie的开发。

2. 压缩Trie (compressed trie)

压缩Trie类似于标准Trie，但它能保证trie中的每个内部结点至少有两个子节点(根结点除外)。通过把单子结点链压缩进叶子节点来执行这个规则。

压缩Trie的定义

冗余结点(redundant node)：如果T的一个非根内部结点v只有一个子结点，那么我们称v是冗余的。

冗余链(redundant link)：如上标准Trie图中，内部结点e只有一个内部子结点l，而l也只有一个叶子结点。那么e-l-l就构成了一条冗余链。

压缩(compressed)：对于冗余链 v1- v2- v3- ... -vn，我们可以用单边v1-vn来替代。

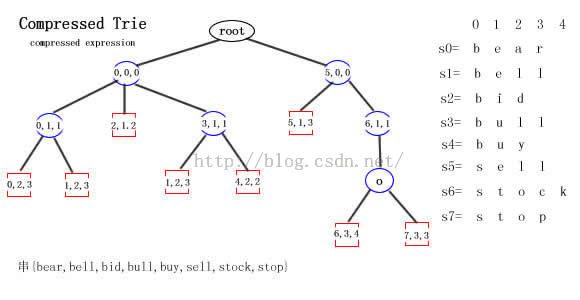
对上面标准Trie的图压缩之后，形成了Compressed Trie的字符表示图如下：

压缩Trie的性质和优势：

与标准Trie比较，压缩Trie的结点数与串的个数成正比了，而不是与串的总长度成正比。一棵存储来自大小为d的字母表中的s个串的结合T的压缩trie具有如下性质：

(1) T中的每个内部结点至少有两个子结点，至多有d个子结点。

(2) T有s个外部结点。

(3) T中的结点数为O(s)

存储空间从标准Trie的O(n)降低到压缩后的O(s)，其中n为集合T中总字符串长度，s为T中的字符串个数。

压缩Trie的压缩表示

上面的图是压缩Trie的字符串表示。相比标准Trie而言，确实少了不少结点。但是细心的读者会发现，叶子结点中的字符数量增加了，比如结点ell，那么这种压缩空间的效率当然会打折扣了。那么有什么好办法呢，这里我们介绍一种压缩表示方法。即把所有结点中的字符串用三元组的形式表示如下图：

其中三元组(i，j，k)表示S[i]的从第j个位置到第k个位置间的子串。比如(5,1,3,)表示S[5][1...3]="ell"。

这种压缩表示的一个巨大的优点就是：无论结点需要存储多长的字串，全部都可以用一个三元组表示，而且三元组所占的空间是固定有限的。但是为了做到这一点，必须有一张辅助索引结构（如上图右侧s0—s7所示）。