回文子串对(扩展kmp-kmp与回文子串)

Problem 1 回文子串对(manacher.cpp/c/pas)

【题目描述】

给定一长度为n的小写字母串，求有多少对回文子串，它们的交集非空。

一对回文子串的交集非空：[a,b]、[c,d](a≠c或b≠d)为2个回文子串，且[a,b]∩[c,d]≠∅。

【输入格式】

第一行一个整数n表示串长。

第二行长度为n的小写字母串。

【输出格式】

输出一个整数表示答案，答案对1000000007取模。

【样例输入】

4

babb

【样例输出】

6

【数据范围】

对于30%的数据，n<=1000

另有10%的数据，串里仅含一种字母。

对于100%的数据，n<=2*10^6

 

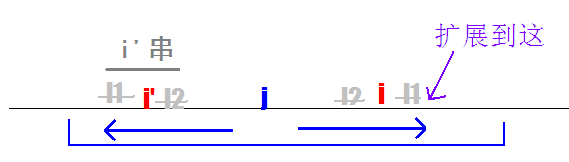
找到最前面的max(r[j]+j),映射过去

设r[i]表示以i点为中心点的最长回文子串

则如图：

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<iostream>
#include<functional>
#include<algorithm>
using namespace std;
#define F (1000000007)
#define MAXN (2000000+10)
using namespace std;
long long r[MAXN],n,L[MAXN][2],R[MAXN][3];
char s[MAXN];
int main()
{
	freopen("manacher.in","r",stdin);
	freopen("manacher.out","w",stdout);
	scanf("%d%s",&n,s+1);
	memset(r,0,sizeof(r));
	memset(L,0,sizeof(L));
	memset(R,0,sizeof(R));
	int j=0;
	for (int i=1;i<=n;i++)
	{
		if (r[j]+j>i) r[i]=min(r[j-(i-j)],j+r[j]-i);
		while (i-r[i]>1&&i+r[i]<n&&s[i-r[i]-1]==s[i+r[i]+1]) r[i]++;
		if (r[i]+i>r[j]+j) j=i;	
		L[i-r[i]][0]+=1;
		L[i+1][0]-=1;
		R[i][0]++;
		R[i+r[i]+1][0]--;		
	}
//	for (int i=1;i<=n;i++) cout<<r[i]<<' ';cout<<endl;
	j=0;memset(r,0,sizeof(r));
	for (int i=1;i<n;i++)
	{
		if (r[j]+j>i) r[i]=min(r[j-(i-j)],j+r[j]-i);
		while (i-r[i]>0&&i+r[i]<=n&&s[i+1-r[i]-1]==s[i+r[i]+1]) r[i]++;
		if (r[i]+i>r[j]+j) j=i;
		L[i+1-r[i]][0]+=1;
		L[i+1][0]-=1;
		R[i+1][0]++;
		R[i+r[i]+1][0]--;		
	}
/*	
	for (int i=1;i<=n;i++) cout<<L[i][0]<<' ';cout<<endl;
	for (int i=1;i<=n;i++) cout<<R[i][0]<<' ';cout<<endl;
*/	
	for (int i=1;i<=n;i++) L[i][1]=L[i][0]+L[i-1][1];
	for (int j=1;j<=2;j++)
		for (int i=1;i<=n;i++)
			R[i][j]=R[i-1][j]+R[i][j-1];
	long long ans=0;
	for (int i=1;i<=n;i++)
		ans=(ans+L[i][1]*R[i-1][2])%F;
	long long tot=0;
	if (R[n][2]%2) tot=(((R[n][2]-1)/2)%F)*((R[n][2])%F)%F;
	else tot=(((R[n][2])/2)%F)*((R[n][2]-1)%F)%F;
//	cout<<tot<<' '<<ans<<endl;
	
	cout<<((tot-ans+F)%F)<<endl;
	return 0;
}