射线和平面的交点
1.1 程序算法:
/** Tests whether this ray intersects the given plane.
@returns A pair structure where the first element indicates whether
an intersection occurs, and if true, the second element will
indicate the distance along the ray at which it intersects.
This can be converted to a point in space by calling getPoint().
*/
//-----------------------------------------------------------------------
std::pair<bool, Real> Math::intersects(const Ray& ray, const Plane& plane)
{
Real denom = plane.normal.dotProduct(ray.getDirection());
平面法向量和射线的方向—点乘,= |ray.getDir()|*cosa;(normal为单位向量)
射线在平面法向量上的分量—标量长度
if (Math::Abs(denom) < std::numeric_limits<Real>::epsilon())
{
// Parallel
return std::pair<bool, Real>(false, 0);
}
else
{
Real nom = plane.normal.dotProduct(ray.getOrigin()) + plane.d
Cosa = d/t è t = d/cosa , 由此可以判断:nom为起点到平面的距离d,denom为cosa
plane.normal.dotProduct(ray.getOrigin())为向量(射线起点)在平面法向量上的投影
Real t = -(nom/denom);
return std::pair<bool, Real>(t >= 0, t);
}
}
1.2 理论分析
射线的表示方法
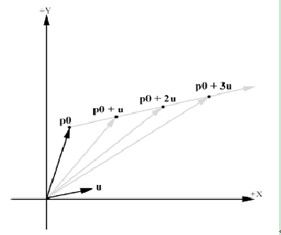
p(t) = p0 + tu;
其中p0是射线的起始点,u是射线的方向向量(需要单位化),t在[0,+无穷]
面的表示方法
由上图可以知道
n(p-p0) = 0;
设d = -np0 由此可以知道,d的几何意义
所以有:np+d = 0;为平面方程,其中p为平面上的任意一点,n为平面的单位法向量,
如果空间中一点Px,如果nPx + d = 0,那么Px在(np+d=0)表示的平面上,如果大于0,该点在平面的上面(法线所指的方向),如果小于0,该点在平面的下面。
3.求射线和平面的交点
要求利用上面所介绍的射线和面的交点只要把p(t)代入(np+d=0)这个方程,这样我们就得到
np(t)+d=0;
n(p0+tu)+d=0;
np0+tnu+d=0;
t=(-d-np0)/nu;
如果t大于等于0说明射线和面有交点,根据p(t)=p0+tu;
