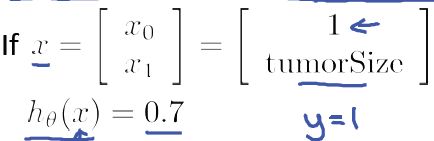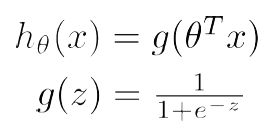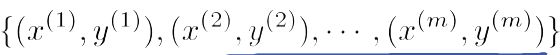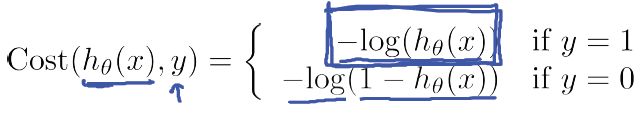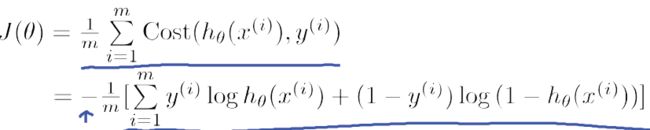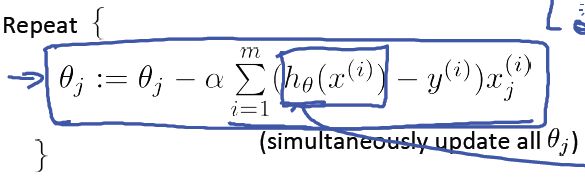逻辑回归与梯度下降法
转载自:http://www.cnblogs.com/yysblog/p/3268508.html
一、逻辑回归
1) Classification(分类)
分类问题举例:
- 邮件:垃圾邮件/非垃圾邮件?
- 在线交易:是否欺诈(是/否)?
- 肿瘤:恶性/良性?
以上问题可以称之为二分类问题,可以用如下形式定义:
其中0称之为负例,1称之为正例。
对于多分类问题,可以如下定义因变量y:
如果分类器用的是回归模型,并且已经训练好了一个模型,可以设置一个阈值:
- 如果hθ(x)≥0.5,则预测y=1,既y属于正例;
- 如果hθ(x)<0.5,则预测y=0,既y属于负例;
如果是线性回归模型,对于肿瘤这个二分类问题,图形表示如下:
但是对于二分类问题来说,线性回归模型的Hypothesis输出值hθ(x)可以大于1也可以小于0。
这个时候我们引出逻辑回归,逻辑回归的Hypothesis输出介于0与1之间,既:
注: 以下引自李航博士《统计学习方法》1.8节关于分类问题的一点描述:
分类是监督学习的一个核心问题,在监督学习中,当输出变量Y取有限个离散值时,预测问题便成为分类问题。这时,输入变量X可以是离散的,也可以是连续的。监督学习从数据中学习一个分类模型或分类决策函数,称为分类器(classifier)。分类器对新的输入进行输出的预测(prediction),称为分类(classification).
2) Hypothesis Representation
逻辑回归模型:
上一节谈到,我们需要将Hypothesis的输出界定在0和1之间,既:
但是线性回归无法做到,这里我们引入一个函数g, 令逻辑回归的Hypothesis表示为:
这里g称为Sigmoid function或者Logistic function, 具体表达式为:
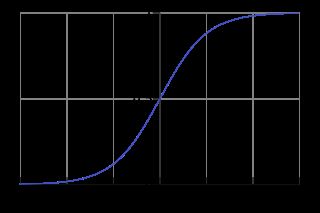
Sigmoid 函数在有个很漂亮的“S"形,如下图所示(引自维基百科):
综合上述两式,我们得到逻辑回归模型的数学表达式:
其中θ是参数。
Hypothesis输出的直观解释:
hθ(x) = 对于给定的输入x,y=1时估计的概率
例如,对于肿瘤(恶性/良性),如果输入变量(特征)是肿瘤的大小:
这里Hypothesis表示的是”病人的肿瘤有70%的可能是恶性的“。
较正式的说法可以如下表示:
给定输入x,参数化的θ(参数空间), y=1时的概率。
数学上可以如下表示:
对于因变量y=0或1这样的二分类问题:
3) Decision boundary(决策边界)
如上节所述,逻辑回归模型可以如下表示:
假设给定的阈值是0.5,当hθ(x)≥0.5时, y = 1;
当hθ(x)<0.5时,y = 0;
再次回顾sigmoid function的图形,也就是g(z)的图形:
当g(z)≥0.5时, z≥0;
对于hθ(x)=g(θTx)≥0.5, 则θTx≥0, 此时意味着预估y=1;
反之,当预测y = 0时,θTx<0;
我们可以认为θTx = 0是一个决策边界,当它大于0或小于0时,逻辑回归模型分别预测不同的分类结果。例如,
θ0,θ1,θ2分别取-3, 1, 1,
则当−3+x1+x2≥0时, y = 1; 则x1+x2 =3是一个决策边界,图形表示如下:
上述只是一个线性的决策边界,当hθ(x)更复杂的时候,我们可以得到非线性的决策边界,例如:
这里当x21+x22≥1时,y=1,决策边界是一个圆形,如下图所示:
更复杂的例子,请参考官方PPT,这里就不再举例了。
4) Cost function(代价函数,成本函数)
逻辑回归概览:
逻辑回归是一种有监督的学习方法,因此有训练集:
对于这m个训练样本来说,每个样本都包含n+1个特征:
其中x∈Rn+1, x0=1,y∈{0,1}.
Hypothesis可表示为:
hθ(x)=11+e−θTx
与线性回归相似,我们的问题是如何选择合适的参数θ?
Cost Function:
线性回归的Cost Function定义为:
这里可以把12(hθ(x(i))−y(i))2简写为Cost(hθ(x(i),y),更简化的表达式为:
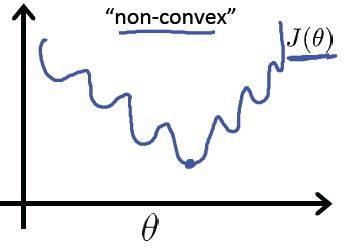
如果和线性回归相似,这里取 hθ(x)=11+e−θTx,会存在一个问题,也就是逻辑回归的Cost Function是“非凸”的,如下图所示:
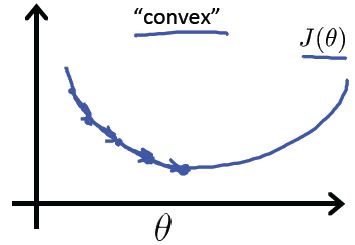
我们知道,线性回归的Cost Function是凸函数,具有碗状的形状,而凸函数具有良好的性质:对于凸函数来说局部最小值点即为全局最小值点,因此只要能求得这类函数的一个最小值点,该点一定为全局最小值点。
因此,上述的Cost Function对于逻辑回归是不可行的,我们需要其他形式的Cost Function来保证逻辑回归的成本函数是凸函数。
这里补充一段李航博士《统计学习方法》里关于Cost Function或者损失函数(loss function)的说明,大家就可以理解Cost Function不限于一种方式,而是有多种方式可选,以下摘自书中的1.3.2小节:
监督学习问题是在假设空间F中选取模型f作为决策函数,对于给定的输入X,由f(X)给出相应的输出Y,这个输出的预测值f(X)与真实值Y可能一致也可能不一致,用一个损失函数(loss function)或代价函数(cost function)来度量预测错误的程度。损失函数是f(X)和Y的非负实值函数,记作L(Y, f(X)).
统计学习中常用的损失函数有以下几种:
(1) 0-1损失函数(0-1 loss function):
L(Y,f(X))={1,0,Y≠f(X)Y=f(X)
(2) 平方损失函数(quadratic loss function)
L(Y,f(X))=(Y−f(X))2
(3) 绝对损失函数(absolute loss function)
L(Y,f(X))=|Y−f(X)|
(4) 对数损失函数(logarithmic loss function) 或对数似然损失函数(log-likelihood loss function)
L(Y,P(Y|X))=−logP(Y|X)
损失函数越小,模型就越好。
逻辑回归的Cost Function:
基于上节的描述和补充,这里我们选择对数似然损失函数作为逻辑回归的Cost Function:
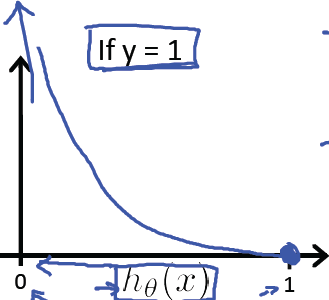
直观的来解释这个Cost Function,首先看当y=1的情况:
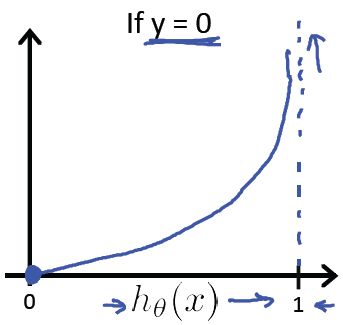
直观来看, 如果y = 1, hθ(x)=1,则Cost = 0,也就是预测的值和真实的值完全相等的时候Cost =0;
但是,当hθ(x)→0时, Cost→∞
直观来看,由于预测的结果南辕北辙:
如果hθ(x)=0, 也就是预测P(y=1|x;θ)=0,也就是y=1的概率是0,但是实际上y = 1
因此对于这个学习算法给予一个很大的Cost的惩罚。
同理对于y=0的情况也适用:
5) Simplified cost function and gradient descent(简化版代价函数及梯度下降算法)
逻辑回归的Cost Function可以表示为:
由于y 只能等于0或1,所以可以将逻辑回归中的Cost function的两个公式合并,具体推导如下:
故逻辑回归的Cost function可简化为:
对于这个公式,这里稍微补充一点,注意中括号中的公式正是对逻辑回归进行最大似然估计中的最大似然函数,对于最大似然函数求最大值,从而得到参数(\theta\)的估计值。反过来,这里为了求一个合适的参数,需要最小化Cost function,也就是:
而对于新的变量x来说,就是根据hθ(x)的公式输出结果:
与线性回归相似,这里我们采用梯度下降算法来学习参数θ,对于J(θ):
目标是最小化J(θ),则梯度下降算法的如下:
对J(θ)求导后,梯度下降算法如下:
注意,这个算法和线性回归里的梯度下降算法几乎是一致的,除了hθ(x)的表示不同。
6) Advanced optimization(其他优化算法)
优化算法:
给定参数θ,我们可以写成代码来计算:
优化算法除了梯度下降算法外,还包括:
- Conjugate gradient method(共轭梯度法)
- Quasi-Newton method(拟牛顿法)
- BFGS method
- L-BFGS(Limited-memory BFGS)
后二者由拟牛顿法引申出来,与梯度下降算法相比,这些算法的优点是:
第一,不需要手动的选择步长;
第二,通常比梯度下降算法快;
但是缺点是更复杂-更复杂也是缺点吗?其实也算不上,关于这些优化算法,推荐有兴趣的同学看看52nlp上这个系列的文章:无约束最优化,作者是我的师兄,更深入的了解可以参考这篇文章中推荐的两本书:
用于解无约束优化算法的Quasi-Newton Method中的LBFGS算法到这里总算初步介绍完了,不过这里笔者要承认的是这篇文档省略了许多内容,包括算法收敛性的证明以及收敛速度证明等许多内容。因此读者若希望对这一块有一个更深入的认识可以参考以下两本书:
1) Numerical Methods for Unconstrained Optimization and Nonlinear Equations(J.E. Dennis Jr. Robert B. Schnabel)
2) Numerical Optimization(Jorge Nocedal Stephen J. Wright)
7) Multi-class classification: One-vs-all(多类分类问题)
多类分类问题举例:
电子邮件分类/标注: 工作邮件,朋友邮件,家庭邮件,爱好邮件
医疗图表(medical diagrams): 没有生病,着凉,流感
天气:晴天,多云,雨,雪
二类分类问题如下图所示:
多类分类问题如下所示:
One-vs-all(one-vs-rest):
对于多类分类问题,可以将其看做成二类分类问题:保留其中的一类,剩下的作为另一类。例如,对于下面这个例子:
可以分别计算其中一类相对于其他类的概率:
总结-One-vs-all方法框架:
对于每一个类 i 训练一个逻辑回归模型的分类器h(i)θ(x),并且预测 y = i时的概率;
对于一个新的输入变量x, 分别对每一个类进行预测,取概率最大的那个类作为分类结果:
二、梯度下降法
现在,我们有了优化目标,即最小化负对数似然函数L(w)。从上一节我们知道不能直接使用其导数为0来求解最优值,我们现在来介绍一种非常常用的求近似最优解的方法:梯度下降法。
梯度下降法的思路其实很简单,假设我们有一个如下图所示的凸函数:
我们首先在函数上任选一点,计算其损失(即我们上面的L(w)) ,然后按照某一规则寻找更低的一点计算新的损失,只要新损失更小(最小化问题),我们就继续下降,直到达到一个可接受的优化目标。
我们的L(w)本质上与上图的求解方式类似,下降方向就是梯度方向ΔL(w)的反方向,即当函数处在上升阶段时,我们往左边下降,函数下降阶段我们往右边下降(参看上图)。
梯度下降方法分为两个部分,第一部分是整体上,我们使用某步长不断下降求损失函数,第二部分是为了防止步长太长导致最后无法收敛,每次当损失上升的时候都调整步长。
以下是梯度下降求解L(w)最优值的过程:
1)首先建立坐标系,横轴是我们的目标参数w,纵轴是当前参数情况下的损失L(w):
建立坐标系后,首先随机取一个参数W1,同时获得初始损失L1。
2)根据梯度公式,获得初始的梯度D1,同时根据梯度方向获得初始的下降方向Direction1(即往正方像下降):
3)现在,我们有了梯度下降的方向、有了初始损失,下一步只需要按照某步长C来往右边调整W即可,然后对比两个损失,当他们的差比较小的时候,说明趋于最优值了。
但是这里步长不好取,加入正好把W下降到对面,那损失的差虽然很小,显然没有趋于最优,再或者步长取的过长,损失反而上升了,也不行,所以我们第三步的主要目的是调整一个稳定的步长,根据该步长获得新的W。
所以第三步作为单独的一个目的,要分四小步来做:
3-1)设置一个初始的步长C1,根据该步长按照梯度对参数W1进行下降得到W2=W1+D1∗Direction1:
图中W2即为新的参数,根据这个新的参数可以获得新的损失L2,我们可以看到损失下降的值为b=L1−L2。
为了保证每次下降的质量,我们需要对b进行一些限制。
3-2)假如我们按照当前梯度和步长完全下降,即不考虑约束条件,最大可能下降的值为S=<D1,W2−W1>=<D1,a>,如下图中的S所示:
我们当然不可能要求损失下降的长度为S,这里只需要L1−L2大于某个指定的关于S的比例即可,我们这里设置该比例为“容忍度” B(B为0到1之间的值)。即要满足的条件是:
3-3)如果不能满足 3-2 中的条件,说明我们的步长有问题,通常是步长太长了,我们需要调整该步长。我们设定一个“折半因子” A(A为0到1之间的值),把当前的步长C1 进行“折半”,即 C2=A∗C1,按照新的步长进行第 3-1 步。
3-4)如果满足 3-2 中的条件,我们直接返回新的W2,即当前的下降成功,进入第 4步 。
4)从第 3 步我们得到了新的W之后,按照新的参数计算新的损失 L,对比新的损失与旧损失之间的差值,如果差值较小达到某阈值,说明拟合成功,否则继续进行第 2 步。
以上内容就是基本的梯度下降法的使用了,对于基本梯度下降的改进有很多,其他的博主也不是很熟,就暂时不讨论了,我们通常实践中用的时候,都是用一些开源的大师写好的算法,一般很少需要深度改进,比如使用libsvm可以直接求解逻辑回归。