Trie树
Trie树也称字典树,因为其效率很高,所以在在字符串查找、前缀匹配等中应用很广泛,其高效率是以空间为代价的。
一.Trie树的原理
利用串构建一个字典树,这个字典树保存了串的公共前缀信息,因此可以降低查询操作的复杂度。
下面以英文单词构建的字典树为例,这棵Trie树中每个结点包括26个孩子结点,因为总共有26个英文字母(假设单词都是小写字母组成)。
则可声明包含Trie树的结点信息的结构体:
#define MAX 26
typedef struct TrieNode //Trie结点声明
{
bool isStr; //标记该结点处是否构成单词
struct TrieNode *next[MAX]; //儿子分支
}Trie;
其中next是一个指针数组,存放着指向各个孩子结点的指针。
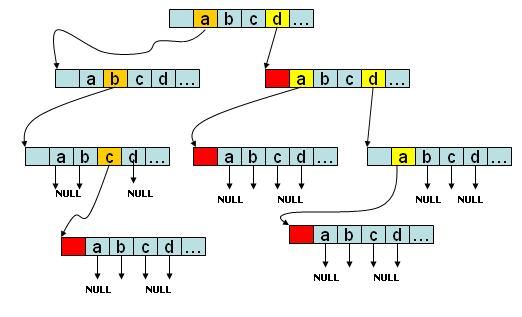
如给出字符串"abc","ab","bd","dda",根据该字符串序列构建一棵Trie树。则构建的树如下:
Trie树的根结点不包含任何信息,第一个字符串为"abc",第一个字母为'a',因此根结点中数组next下标为'a'-97的值不为NULL,其他同理,构建的Trie树如图所示,红色结点表示在该处可以构成一个单词。很显然,如果要查找单词"abc"是否存在,查找长度则为O(len),len为要查找的字符串的长度。而若采用一般的逐个匹配查找,则查找长度为O(len*n),n为字符串的个数。显然基于Trie树的查找效率要高很多。
但是却是以空间为代价的,比如图中每个结点所占的空间都为(26*4+1)Byte=105Byte,那么这棵Trie树所占的空间则为105*8Byte=840Byte,而普通的逐个查找所占空间只需(3+2+2+3)Byte=10Byte。
网上有很多关于trie树的资料,其核心思想就时拿空间换取时间,很适合搜索前缀子窜,时间效率比较高,主要是占用空间比较大。为什么会这样呢?看下trie树的结构就知道拉。
如图所示,该trie树存有abc、d、da、dda四个字符串,如果是字符串会在节点的尾部进行标记。没有后续字符的branch分支指向NULL
已知n个由小写字母构成的平均长度为10的单词,判断其中是否存在某个串为另一个串的前缀子串。下面对比3种方法:
1. 最容易想到的:即从字符串集中从头往后搜,看每个字符串是否为字符串集中某个字符串的前缀,复杂度为O(n^2)。
2. 使用hash:我们用hash存下所有字符串的所有的前缀子串。建立存有子串hash的复杂度为O(n*len)。查询的复杂度为O(n)* O(1)= O(n)。
3. 使用trie:因为当查询如字符串abc是否为某个字符串的前缀时,显然以b,c,d....等不是以a开头的字符串就不用查找了。所以建立trie的复杂度为O(n*len),而建立+查询在trie中是可以同时执行的,建立的过程也就可以成为查询的过程,hash就不能实现这个功能。所以总的复杂度为O(n*len),实际查询的复杂度只是O(len)。
解释一下hash为什么不能将建立与查询同时执行,例如有串:911,911456输入,如果要同时执行建立与查询,过程就是查询911,没有,然后存入9、91、911,查询911456,没有然后存入9114、91145、911456,而程序没有记忆功能,并不知道911在输入数据中出现过。所以用hash必须先存入所有子串,然后for循环查询。
而trie树便可以,存入911后,已经记录911为出现的字符串,在存入911456的过程中就能发现而输出答案;倒过来亦可以,先存入911456,在存入911时,当指针指向最后一个1时,程序会发现这个1已经存在,说明911必定是某个字符串的前缀,
二.Trie树的操作
在Trie树中主要有3个操作,插入、查找和删除。一般情况下Trie树中很少存在删除单独某个结点的情况,因此只考虑删除整棵树。
1.插入
假设存在字符串str,Trie树的根结点为root。i=0,p=root。
1)取str[i],判断p->next[str[i]-97]是否为空,若为空,则建立结点temp,并将p->next[str[i]-97]指向temp,然后p指向temp;
若不为空,则p=p->next[str[i]-97];
2)i++,继续取str[i],循环1)中的操作,直到遇到结束符'\0',此时将当前结点p中的isStr置为true。
2.查找
假设要查找的字符串为str,Trie树的根结点为root,i=0,p=root
1)取str[i],判断判断p->next[str[i]-97]是否为空,若为空,则返回false;若不为空,则p=p->next[str[i]-97],继续取字符。
2)重复1)中的操作直到遇到结束符'\0',若当前结点p不为空并且isStr为true,则返回true,否则返回false。
3.删除
删除可以以递归的形式进行删除。
测试程序:
/*Trie树(字典树)*/
#include <iostream>
#include<cstdlib>
#define MAX 26
using namespace std;
typedef struct TrieNode //Trie结点声明
{
bool isStr; //标记该结点处是否构成单词
struct TrieNode *next[MAX]; //儿子分支
}Trie;
void insert(Trie *root,const char *s) //将单词s插入到字典树中
{
if(root==NULL||*s=='\0')
return;
int i;
Trie *p=root;
while(*s!='\0')
{
if(p->next[*s-'a']==NULL) //如果不存在,则建立结点
{
Trie *temp=(Trie *)malloc(sizeof(Trie));
for(i=0;i<MAX;i++)
{
temp->next[i]=NULL;
}
temp->isStr=false;
p->next[*s-'a']=temp;
p=p->next[*s-'a'];
}
else
{
p=p->next[*s-'a'];
}
s++;
}
p->isStr=true; //单词结束的地方标记此处可以构成一个单词
}
int search(Trie *root,const char *s) //查找某个单词是否已经存在
{
Trie *p=root;
while(p!=NULL&&*s!='\0')
{
p=p->next[*s-'a'];
s++;
}
return (p!=NULL&&p->isStr==true); //在单词结束处的标记为true时,单词才存在
}
void del(Trie *root) //释放整个字典树占的堆区空间
{
int i;
for(i=0;i<MAX;i++)
{
if(root->next[i]!=NULL)
{
del(root->next[i]);
}
}
free(root);
}
int main(int argc, char *argv[])
{
int i;
int n,m; //n为建立Trie树输入的单词数,m为要查找的单词数
char s[100];
Trie *root= (Trie *)malloc(sizeof(Trie));
for(i=0;i<MAX;i++)
{
root->next[i]=NULL;
}
root->isStr=false;
scanf("%d",&n);
getchar();
for(i=0;i<n;i++) //先建立字典树
{
scanf("%s",s);
insert(root,s);
}
while(scanf("%d",&m)!=EOF)
{
for(i=0;i<m;i++) //查找
{
scanf("%s",s);
if(search(root,s)==1)
printf("YES\n");
else
printf("NO\n");
}
printf("\n");
}
del(root); //释放空间很重要
return 0;
}
原文地址:http://www.cnblogs.com/dolphin0520/archive/2011/10/11/2207886.html
参考:http://blog.163.com/mageng11@126/blog/static/14080837420119544046207/
参考:http://dongxicheng.org/structure/trietree/