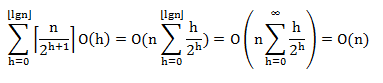算法学习笔记----堆排序

  堆是一个数组，可以看成一个近似的完全二叉树，除了最底层外，其余各层都是充满的，而且是从左到右填充。假设数组A[1..A.hep_size]是一个对，给定一个结点的下标i，很容计算出其父节点、左孩子和右孩子的下标，如下所示（这里的数组下标是从1开始）：

  在C语言中数组下标是从0开始的，因此在计算父节点、左右子节点时的公式和上图中有所不同，如下图所示：

  二叉堆可以分为两种形式：最大堆和最小堆。在最大堆中，除了根节点以外所有的节点i都要满足：A[PARENT(i)]≥A[i]。最小堆则刚好相反。下面的讨论以最大堆为例。

一、维护堆的性质

  MAX-HEAPIFY是用于维护最大堆性质的重要过程。假设根节点为LEFT(i)和RIGHT(i)的二叉树都是最大堆，但此时A[i]有可能小于其孩子，这就违背了最大堆的性质。这时为了维护最大堆的性质，将索引为i的节点和其孩子中最大的节点互换。假设i的左孩子较大，此时需要将节点i和其左孩子互换，互换后可能会导致以节点i的左孩子为根节点的最大堆违背了最大堆的性质，因此需要继续调整节点的顺序，直到根节点大于左右孩子节点或处理到叶子节点为止。以下面的最大堆（下标是从0开始）为例：

  在阴影部分的节点i=1处，A[1]违背了最大堆性质，A[1]及其左右孩子节点中最大的是节点i=3，因此将节点i=2和节点i=3互换，使节点i=2恢复最大堆性质，如下图所示：

  互换后，节点i=3的值小于其右孩子i=8的节点，因此需要将这两个节点互换，使节点i=3恢复最大堆性质，如下图所示：

  互换后，节点i=8为叶子节点，没有子节点了，也就不再有新的数据交换了。

  接下来计算 MAX-HEAPIFY的时间复杂度。每个孩子的子树的大小至多为2n/3，最坏的情况发生在树的最底层恰好半满的时候，因为最大堆是一个类似完全二叉树的数组，左右子树的高度最多相差1，所以在子树的高度较高的一边时执行的次数可能越多。

  下面证明一下，为什么每个子树的大小至多为2n/3。假设一个最大堆构成的完全二叉树的高度为h，如果完全充满的话，堆的元素个数为2^(h+1)-1 。我们在上面提到过，根节点的左右子树的高度最多相差为1，因此左右子树差距最大的情况发生在其中一个子树的最后一层充满，而另一个子树的对应的层为空。假设最大的子树为左子树，则左子树的元素个数为2^h-1，而右子树的元素个数为2^(h-1)-1，假设总的个数为n，左子树的个数为left_count, 右子树的个数为righ_count，计算左子树所占的最大比重，如下所示：

  从上面的步骤中可以看出，总的时间复杂度包括调整A[i]、A[LEFT(i)]和A[RIGHT(i)]的关系的时间代价Θ(1)，加上在一颗以i的一个孩子为根节点的子树上执行维护最大堆的操作的时间代价(这里假设递归调用会发生）。因为每个孩子的子树的大小至多为2n/3，我们可以用下面的递归式来计算总的运行时间：

T(n)≤T(2n/3)+Θ(1)

 根据主定理（参考这里）的情况2，上述递归式的解为T(n)=O(lgn)。也就是说，对于一个树高度为h的的节点来说， MAX-HEAPIFY需要的时间复杂度为O(h)。

  下面是代码实现，分别利用递归和循环来完成。

  递归版本：

#include <stdio.h>

void exchange(int *a, int i, int j)
{
    a[i] ^= a[j];
    a[j] ^= a[i];
    a[i] ^= a[j];
}

int left_child(int i)
{
    return (2*(i + 1) - 1);
}

int right_child(int i)
{
    return (2*(i + 1) + 1 - 1);
}

void max_heapify(int *a, int len, int index)
{
    int l, r;
    int largest = index;
    
    l = left_child(index);
    r = right_child(index);
    
    if ((l < len) && (a[l] > a[largest])) {
        largest = l;
    }
    if ((r < len) && (a[r] > a[largest])) {
        largest = r;
    }
    
    if (largest != index) {
        exchange(a, largest, index);
        max_heapify(a, len, largest);
    }
}

int main(void)
{
    int source[] = {16, 4, 10, 14, 7, 9, 3, 2, 8, 1};
    int i;
    
    max_heapify(source, sizeof(source) / sizeof(source[0]), 1);
    
    for (i = 0; i < sizeof(source) / sizeof(source[0]); ++i) {
        printf("%d ", source[i]);
    }
    printf("\n");
    return 0;
}

  循环版本：

void max_heapify(int *a, int len, int index)
{
    int l, r;
    int largest = index;
    
    while(index < len) {
        l = left_child(index);
        r = right_child(index);
    
        if ((l < len) && (a[l] > a[largest])) {
            largest = l;
        }
        if ((r < len) && (a[r] > a[largest])) {
            largest = r;
        }
    
        if (largest != index) {
            exchange(a, largest, index);
            //max_heapify(a, len, largest);
            index = largest;
            continue;
        }
        
        break;
    }
}

二、建堆

  我们可以用自底向上的方法利用过程MAX-HEAPIFY把一个大小为n=A.length的数组A[1..n]转换为最大堆。其过程是：从i=⌊A.length/2⌋开始到1，循环调用MAX-HEAPIFY过程来构建堆。为什么要从i=⌊A.length/2⌋开始呢？因为⌊n/2⌋+1、⌊n/2⌋+2,...、n都是叶子节点，所以在循环开始前这些节点是平凡最大堆的根节点。从这些节点开始循环调用MAX-HEAPIFY来维护以节点i为根节点的最大堆的性质，过程终止时每个节点都是一个最大堆的根。特别需要指出的是，节点1就是最大的堆的根节点。

  下面我们来证明为什么⌊n/2⌋+1、⌊n/2⌋+2,...、n这些节点都是叶子节点。为了简化，我们假设规模为n的堆刚好完全填充，其高度为h，则根据高度计算的话，总的节点个数n=2^(h+1)-1。我们知道最后一层的节点都是叶子节点，除去最后一层，树的高度为h-1，最后一层之上的节点总和为2^h-1=(1/2)n-(1/2)=⌊n/2⌋。因此最后一层的节点是从⌊n/2⌋+1开始的。

  建堆的代码实现如下所示：

void build_max_heap(int *a, int len)
{
    int i;
    
    for (i = len / 2; i >= 0; --i) {
        max_heapify(a, len, i);
    }
}

  为什么build_max_heap()中循环控制变量i来说，它是从 ⌊n/2⌋到0递减，而不是从0到⌊n/2⌋递增呢？这是《算法导论》中的一个练习题。个人的理解是：如果是从上到下，发生节点交换时不仅要考虑向下维护最大堆，也要考虑向上维护最大堆，因为交换后的根节点的值可能大于其父节点，这样导致先前做的维护工作浪费了，还要重新开始从上开始向下维护。

  可以用下面的方法简单评估build_max_heap()运行时间的上界。每次调用max_headpify()的时间复杂度为O(lgn)，build_max_heap()需要O(n)次这样的调用，因此总的时间复杂度为O(nlgn)。当然这个上界虽然正确，但不是渐近紧确的。

  在更进一步计算紧确的界之前，要先证明：对于任一包含n个元素的堆中，至多有⌈n/2^(h+1)⌉个高度为h的结点。注意：这里的高度h和我们说的堆的高度不是一回事，这里的高度为当前节点到叶子节点最长简单路径上的数目。我们在前面证明过从⌊n/2⌋+1到n的结点是叶子节点，也就是说最后一层（即高度为0的结点）的节点至多⌈n/2⌉个。将h=0代入⌈n/2^(h+1)⌉中得⌈n/2^(h+1)⌉=⌈n/2⌉，所以在h=0时成立。当h=1时，我们把最后一层之上的节点看做是一个新的堆，此时新的堆的数量n'=⌊n/2⌋，新的堆的最后一层的节点至多为⌈n'/2⌉=⌈⌊n’/2⌋/2⌉≤⌈n/2^(1+1)⌉，新的堆的最后一层的节点相当于原来的堆中高度为1的节点。以此类推当高度为h时，节点至为⌈⌊n/2⌋/2^h⌉≤⌈n/2^(h+1)⌉。

  包含n个元素的的堆的高度为⌊lgn⌋，高度为h的堆最多包含⌈n/2^(h+1)⌉个节点，在一个高度为h的节点上运行MAX-HEAPIFY的代价为O(h)，我们可以将build_max_heap()的总代价表示为：

  因此，可以在限行时间内，把一个无序的数组构造成一个最大堆。

三、堆排序算法

  有了前面的铺垫，堆排序算法就很好理解了。首先调用BUILD-MAX-HEAP将输入的数组建成最大堆，这时最大的元素就是根节点，将根节点和数组的最后一个元素互换，这样最大的元素就在正确的位置上了。然后在调用MAX-HEAPIFY对剩余的元素进行处理，维护最大堆的性质，直到所有的元素都放在正确的位置上。废话不多说了，直接上代码，如下所示：

void heap_sort(int *a, int len)
{
    int i;
    
    build_max_heap(a, len);
    for (i = len - 1; i >= 1; --i) {
        exchange(a, 0, i);
        max_heapify(a, i, 0);
    }
}

  调用build_max_heap()的时间复杂度为O(n)，n-1次调用max_heapify()的时间复杂度为nlgn，因此总的时间复杂度为O(nlgn)。