Dijkstra算法实现单源最短路径
参考《计算机算法设计与分析(第二版)》王晓东电子工业出版社
大二时地理信息系统实习写过Dijkstra寻找最短路径程序,当时对计算机编程还不熟悉,很多知识都不了解,尤其是算法等,今天重新编了一遍,也较为清楚了。以下是自己零星所想,一些思维片段,或许不容易理解。编程以蔽之。
Dijkstra算法思想:
顶点集合G=(V,E)
已知w[i][j]为边(i,j)的权。当(i,j)∉E时,w[i][j]=INT_MAX最大数,视为无边路径连接
dist[i]表示当前从源到顶点i的最短特殊路径长度。
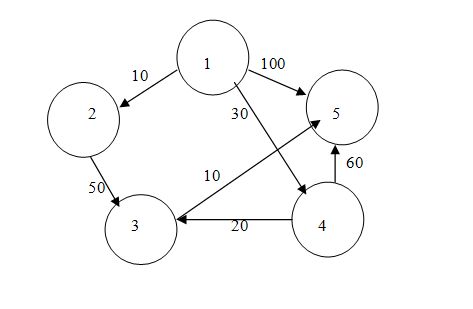
带权有向图G=(V,E),V={1,2,。。。},顶点int start是源
输入为
int n点个数
int start源
w[i][j]为边(i,j)的权。当(i,j)∉E时,w[i][j]=INT_MAX最大数,视为无边路径连接
输出:
Type dist[i]表示当前从源到顶点i的最短特殊路径长度。
int prev[i]表示从start到i点的最短路径中,i点的前一个点。初始第一步:
集合S(贪心集)初始没有元素。
bool s[n] ;
for all s[i];
s[i]=false;s中没有任何元素
for(int i=1;i<=n;i++)
{
dist[i]=w[start][i];//起点到第i点的距离
if(dist[i]==INT_MAX)//起点到i点无边连接
prev[i]=0;//从start到i点的最短路径中,i点的前一个点为0,也就是没有边连接
else prev[i]=start;// start和i点直接相连,也就是说从start到i点的最短路径中,i点的前一个点为start
}
初始化求得start点到各点的直接距离。
置dist[start]=0; //start到自身距离为0
s[start]=true;//此时已经求得经过start点到各点的最短距离,所以将源start加到贪心集s中。
//剩余n-1个点,求经过u点到其余各点的最短距离,直至所有点多加入到s中,此时结束
for(int i=1;i<n;i++)//第i次循环,每次循环加入特殊最短路径
{
int temp=INT_MAX;
int u=start;//源
for(int j=1;j<=n;j++)
{
if((!s[j]) && (dist[j] <temp))
{
u=j;//对每一个点,查看是否在s中,如果还未加入s,并且小于temp
temp = dist[j];
}
}//得到联通start到j(j∈V-S)最短特殊路径的u点(u∈V-S)
//将u加入s
s[u]=true;
for(int j=1;j<=n;j++)
{
if((!s[j]) && (w[u][j] <INT_MAX))
{
Type newdist=dist[u]+w[u][j];
if(newdist < dist[j])
{
dist[j]=newdist;
prev[j]=u;
}
}
}
}
也就是说先假设源start点到各点的连接距离为最短距离,然后判断新加入一个点u,如果通过u点能使连接各点的距离缩短,就将start点到i点的距离更新,且记i点的前一节点为u。把u点加入到s集合中,也就是说,经过s中的点到各点的最短距离和相应路径已经知道,从剩余的V-S中取出联通距离最短的一点u加入到结合S,并判断u是否能使目前start到V-S中最短距离缩短,如果能则修改最短距离dist[i]和V-S各点的前一节点为u。直至所有节点都加入到S,dist就记录了从源到所有其他顶点之间的最短路径长度。
VC++下编程实现
// Dijkstra.cpp : Defines the entry point for the console application.
//
#include "stdafx.h"
#include "stdio.h"
#include "stdlib.h"
#include "vector"
const double INFINITE=99999999;
/************************************************************************************************/
/* 输入为 Dijkstral单源最短路径
* int n 点个数
* int start 源
* weight[i][j] 边(i,j)的权。当(i,j)不属于E时,w[i][j]=INFINITE最大数,视为无联通
*
* 输出:
* Type dist[i] 表示当前从源到顶点i的最短特殊路径长度。
* int prev[i] 表示从start到i点的最短路径中,i点的前一个点。
* 作者:Archie
* 日期:2012年9.2日
*************************************************************************************************/
void Dijkstral(int n,int start,double *w,double dist[],int prev[]);
double weight[]={0.0 ,10.0 , INFINITE , 30 ,100 ,
INFINITE ,0 , 50 , INFINITE ,INFINITE ,
INFINITE ,INFINITE , 0 , INFINITE ,10 ,
INFINITE ,INFINITE , 20 , 0 ,60 ,
INFINITE ,INFINITE , INFINITE , INFINITE ,0 };
int main(int argc, char* argv[])
{
int n=5;
int start=1;
double dist[5];
int prev[5];
Dijkstral(n, start, weight, dist, prev);
for (int i=0;i<n; i++)
{
std::vector<int> path;
path.push_back(i);
int t=prev[i];
while (t!=-1 && t!=start-1)
{
path.push_back(t);
t=prev[t];
}
path.push_back(start-1);
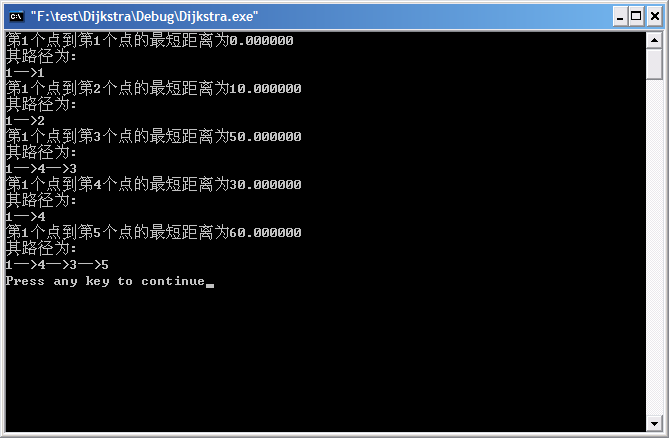
printf("第%d个点到第%d个点的最短距离为%f\n",start,i+1,dist[i]);
printf("其路径为:\n");
for (std::vector<int>::reverse_iterator r_iter=path.rbegin();r_iter!=(path.rend()-1);r_iter++)
printf("%d—>",(int)*r_iter+1);
printf("%d\n",i+1);
}
return 0;
}
void Dijkstral(int n,int start,double *w,double dist[],int prev[])
{
bool *s=new bool[n];
for(int i=1;i<=n;i++)
{
s[i-1]=false; //初始集合S(贪心集)没有元素
dist[i-1]=*(w+(start-1)*n+(i-1)); //起点start到第i点的距离 传进来的数组须连续存放即数组形式a[m][n]
if(dist[i-1]==INFINITE) //起点到i点无边连接
prev[i-1]=-1; //从start到i点的最短路径中,i点的前一个点为-1,也就是没有边连接
else prev[i-1]=start-1; //start和i点直接相连,也就是说从start到i点的最短路径中,i点的前一个点为start
}
// 初始化求得start点到各点的直接距离。
dist[start-1]=0; //start到自身距离为0
s[start-1]=true; //此时已经求得经过start点到各点的最短距离,所以将源start加到贪心集s中。
//剩余n-1个点,循环第i个点u加入s,直至所有点加入到s中
for(i=0;i<n-1;i++)
{
double temp=INFINITE;
int u=start-1;//源
for(int j=0;j<n;j++)
{
if((!s[j]) && (dist[j] <temp))
{
u=j;//对每一个点,查看是否在s中,如果还未加入s,并且小于temp
temp = dist[j];
}
}//得到联通start到j(j∈V-S)最短特殊路径的u点(u∈V-S)
//将u加入s
s[u]=true;
for(j=0;j<n;j++)
{
if((!s[j]) && (*(w+u*n+j) <INFINITE))
{
double newdist=dist[u]+*(w+u*n+j);
if(newdist < dist[j])
{
dist[j]=newdist;
prev[j]=u;
}
}
}
}
if (s!=NULL)
{
delete[]s;
s=NULL;
}
}
针对上图结果