线性代数(七) : 子空间的基与维数

线性空间中基的概念很重要,比如一个子空间中的任意一个向量都可用一组基唯一的表示.有些问题可以通过寻找一组合适的基而大大化简；

1空间的基

直接给出定义：

如果线性空间X中的有限个向量张成X并且本身线性无关,则称他们为X的一组基(basis).

下边对基的定义和性质做一些说明:

(1)由有限个向量x1,...,xn张成线性空间X有基.

证明：假设x1,...,xn线性相关。则存在一个xi可以表示成其他向量的线性组合.把这个向量从向量组中剔除.则剩余的向量仍然可以张成线性空间X

重复这一步骤直到剩下的向量线性无关.显然他们仍然可以张成线性空间X. 所以他们是线性空间X的一组基

(2)定义：如果线性空间X有基,则称X是有限维(finite dimensional)线性空间.

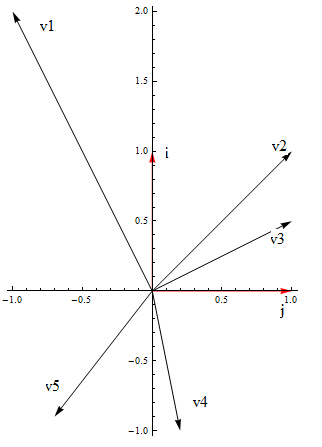
(3)一个有限维的线性空间有无数组基.如下图R^2中的几个不公线的向量.任取他们之中的两个都线性无关的，并且张成R^2(这个结论在上一节证明过)

因此是一组基.

(4)标准基(standard basis) ：在这无数组基中有一组是十分有用的也就是基中的每一个向量都有一个分量是1其他的分量是0,这样的基叫做标准基(如上图中的i和j向量)。

标准基对于很多运算都是很方便的。下面是R^2与R^3中的标准基：

2 线性空间的维数

有限维线性空间X的全体基都包含相同数目的向量,这个数称作X的维数(dimension)记作：

dim X

定义由零向量构成的平凡子空间的维数为0

(i)下面证明每组基都包含相同数目的向量：

证明:设a1,...,an    b1,...,bm 为同一个线性空间下的两组基.

现在回忆上节证明的一个性质：设向量x1,,,,,xn张成线性空间X,若X中的向量y1,...,yj线性无关,则有j<=n.

由这条性质可知,n<=m 并且m<=n 因此n=m。证明结束.

(ii)有限维线性空间中每一组线性无关的向量组都可以扩充为该空间的一组基

证明:假设线性空间X中的一组线性无关向量y1,...,yj不能张成X,则存在x1∈X 不能表示为y1,...,yj的线性组合

把x1添加进去,重复这个过程直到向量组可以张成x 这样就扩充为X的一组基。

这个性质说明我们可以从任意一个线性无关的向量组开始扩充为一组基.

(iii)补空间 : 线性空间X的任意子空间Y在X中都存在一个补空间Z使得任意x∈X都可以唯一的分解为：

x = y + z (y∈Y,z∈) 并且：

dim X = dim Y + dim Z

根据性质(ii)这个是很容易证明的.留给读者自行证明.

3 超平面:

n维线性空间的n-1维线性子空间称为超平面(hyperplane).

如二维空间下的直线和三维空间下的平面都是超平面.