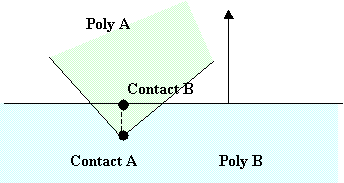
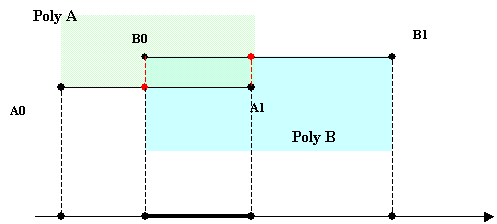
基于2D多边形的碰撞检测和响应(六)

六、计算触点

为了动态的移动刚体，我们需要精确计算两个碰撞多边形之间的触点。对于2D来说这并不复杂，但是在3D场景中会变得非常复杂。在2D情况下，可以考虑两种情况，点和边的相交或者是边和边的相交。

 

这个处理过程几乎不需要教程，但是它非常适合于一个可视化的演示

这里，我只考虑交叠的情况，这个原理也适用于碰撞的情况。

现在给出一个碰撞的法向，在点边接触的情况下，如何求得触点？

对于接触点A，它是直接向前的。我们需要调用一个支撑映射函数，他将返回多边形在制定方向上的最低点，非常类似于第一个例子中的CalculateInterval()函数

int FindSupportPoints(const Vector& N, float t,
                      const Vector* A, int Anum,
                      const Vector& PA, const Vector& VA,
                      const Matrix& OA, Vector* S)
{
    Vector Norm = N ^ OA;
    float d[32];
    float dmin;
    dmin = d[0] = A[0] * Norm;

    for(int i = 1; i < Anum; i ++)
    {
        d[i] = A[i] * Norm;

        if (d[i] < dmin)
        {
            dmin = d[i];
        }
    }

    int Snum = 0;

    const float threshold = 1.0E-3f;

    for(int i = 0; i < Anum; i ++)
    {
        if (d[i] < dmin + threshold)
        {
            S[Snum++] = Transform(A[i], PA, VA, OA, t);
           
            if (Snum == 2)
                return Snum;
        }
    }
    return Snum;
}

这里，函数的第一部分找到多边形的最小值。第二部分简单的找到接近最小值的所有点，因此如果碰撞法线垂直于一条边，将返回两个点。这两个点将以世界坐标存贮，变换函数将确保多边形的触点被转化为世界坐标，并且如果是一个未来的碰撞，这个点将被转化为碰撞时刻的

Vector Transform(const Vector& Vertex, const Vector& P, const Vector& V, const Matrix& xOrient, float t)
{
    // convert point into world space
    Vector T = P + (Vertex * xOrient);

    // collision forwatd in time, need to translate to moment of collision
    if(t > 0.0f)
        T += V * t;
    return T;
}

对于B上的点，你只需要简单地在反方向找到一个支撑点，在以后的处理中我们需要一对位于两个物体上的支撑点来做物理模拟推力并使物体旋转，你可以从上图中发现在不同的碰撞情况下你需要得到的一对触点。

 

现在，调用FindSupportPoint()函数在每个物体上返回一个或两个触点。在一对一触点的情况下，不需要做任何事情，现在，还不支持一对一的接触，但是它能够非常容易的扩展到分离轴算法中。

 

在一对二接触的情况下，它是一个简单的点对边的碰撞，如上图中的第一个图

在二对一接触的情况下，可以同样运用上述情况，除了物体被交换外

在二对二接触的情况下，他是一个边边碰撞，你需要找到两个边的交叠区域。

 

首先对于点边碰撞，在这种情况下，一对碰撞点可以简单的通过将A上的碰撞点投影到B的边上来实现，或者说是B的边上最接近A触点的点

Vector FindClosestPoint(const Vector& V, const Vector& A, const Vector& B, float* pt)
{
    Vector AV = V - A;
    Vector AB = B - A;
   
    float t = (AV * AB) / (AB * AB);

    if (t < 0.0f)
        t = 0.0f;
    else if (t > 1.0f)
        t = 1.0f;

    if (pt) *pt = t;

    Vector P = A + t * AB;
    return P;
}

在边对边碰撞的情况下，处理过程非常类似。只是你需要沿着沿着碰撞法线的垂直方向排序点，并得到两个中间点。然后，将它们投影到另外的边上以便得到一对触点。

有了这些触点，你就可以编写一个基本的刚体系统，物体将比以前更真实的相互碰撞并响应碰撞。