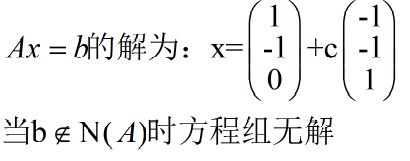线性代数(十二) : 线性方程组Ax=b可解性与解的结构

本节讨论不同的线性方程组的可解性与解的结构.

0 可能需要复习的内容：

零空间与列空间

主元与自由元

1 矩阵的秩与矩阵的行列数

(i)对于一个m行n列的矩阵A， 矩阵的秩表示其列空间的维度,因此rank(A)<=n

(ii)又因为A的列空间中的向量有m个分量。很明显列空间的维数不会大于m,因此rank(A)<=m

2 方程组解的结构

(i)我们将方程组变换为行简化阶梯型。然后找出主元和自由元。

这时令自由元等于0带入方程组中求出主元的值，这组解我们叫做特解(particular solution)下边记做：Xp

(ii)AXp=b  对于A的零空间(N(A))中的向量Xn有： AXn=0 因此有 A(Xp+Xn)=b.

这说明特解与零空间中的向量的和仍然是方程组的解。X=Xp+Xn (Xn∈N(A))

(iii)假设存在X=Xp+Xn (Xn∈N(A))之外的一个解Xs，则AXs=b 则A(Xp-Xs)=0

因此Xp-Xs∈N(A) 因此 Xs = Xp -1Xn这与假设是矛盾的。因此X=Xp+Xn (Xn∈N(A))就是方程组的全部解.记做：

这就是Ax=b的解的通用写法.下边根据矩阵的秩与行列数的关系分几种情况讨论方程组Ax=b的解.

3 满秩的方阵

(i)对于m行n列的矩阵A，当rank(A)=m=n的时候称A为一个满秩的方阵

(ii)由于rank(A)=m,因此参照之前的知识可知矩阵的列向量可以张成整个m维向量空间。因此b取任何值.方程组均有解.

(iii)此时矩阵的列向量线性无关。因此Ax=0只有零向量一个解因此零空间只有零向量。

这样方程组Ax=b的解就是X=Xp了.综上满秩方阵存在一个解.

下面以一个列子说明求解这个特解：

(iv)以后会介绍这种满秩的方阵还有另一个名字就是可逆矩阵。到时会以线性映射的角度再次介绍此时方程组的解的存在性与唯一性。

4 行满秩矩阵

(i)对于m行n列的矩阵A，当rank(A)=m,m<n的时候称A为一个行满秩矩阵

(ii)由于rank(A)=m,因此参照之前的知识可知矩阵的列向量可以张成整个m维向量空间。因此b取任何值.方程组均有解.

(iii)此时方程组存在自由元因此零空间的维度大于0,所以此时方程组有无数的解。X=Xp+Xn (Xn∈N(A))

下边是一个例子：

5 列满秩矩阵

(i)对于m行n列的矩阵A，当rank(A)=n,m>n的时候称A为一个列满秩

(ii)由于rank(A)<m,因此参照之前的知识可知矩阵的列向量不能张成整个m维向量空间。因此b取列空间中的值方程组才有解。

(iii)此时矩阵的列向量线性无关。因此零空间只有零向量。因此如果存在解的话将是一个解。综上列满秩矩阵存在一个解或者0个解

下边是一个例子：

6 行列秩都不满的矩阵

(i)对于m行n列的矩阵A，当rank(A)<n,rank(A)<m这时称为行列秩都不满。
(ii)由于rank(A)<m,因此列向量不能张成整个m维向量空间。因此b取列空间中的值方程组才有解。
(ii)假设b取列空间的值此时方程组存在解.由于rank(A)<n 因此含有自由列因此零空间的维度大于0,所以此时方程组有无数的解。
综上这样的矩阵对应的方程组有0个解或者无数个解。下边是一个例子:

满秩的方阵是一类特殊的也是具有很好的性质的矩阵,接下来几节将会详细介绍