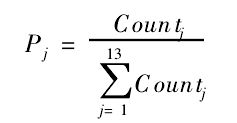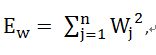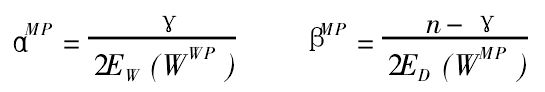下棋机器人视觉系统

对弈机器人的视觉图像处理和识别

张志伟　孔凡让　赵吉文　何清波　吴增荣

(中国科学技术大学精密机械与精密仪器系　安徽合肥230027)

摘　要　　基于视觉的对弈机器人在国内尚无先例,其视觉系统的实现是此研究的关键。提出了彩色空间变换,阈值分割、形态学

骨架化及霍夫变换等图像处理技术对棋局中的棋子进行检测、定位和分割的方法。在棋子识别过程中,为克服棋子摆放方向的随意性,提取棋子旋转不变的径向像素点数特征;用BP神经网络进行识别,并采用贝叶斯正则化方法提高了网络的推广性。实验表明,该方法定位、分割棋子准确无误,识别率较高。

关键词　　对弈机器人　彩色图像处理　BP神经网络　贝叶斯正则化

0　引　言

机器弈棋是人工智能、自动控制、计算机视觉、模式识别等理论与技术的综合应用。最著名的例子就是1997年IBM公司的超级计算机“深蓝”击败了国际象棋世界冠军卡斯帕罗夫。随着机器人和自动控制技术的发展,机器弈棋不仅是用计算机进行思考,已发展到用机器人代替人类进行弈棋过程的各种行为[1, 2]。但目前国内还缺乏真正的具有类人形、可以独立完成弈棋全过程的机器人。我们正在研制的仿人弈象棋机器人可以独立完成所有弈棋动作,它具有人的外形,可以观察识别真实棋局,思考行棋招法,并且具有可以移动棋子的手臂。主要由四个部分组成:视觉系统、博弈系统、控制系统、中枢系统。视觉系统观察棋局图像并加以识别;博弈系统对棋局进行分析推演;控制系统用于操纵移动棋子;中枢系统对各功能进行统一调度,并实现各部分之间的接口和通信。

本文的研究内容是机器人视觉系统的实现。视觉系统相当于机器人的眼睛,其功能是从摄像头拍摄的棋局图像检测出每一个棋子,识别出其颜色和种类,并得到棋子的位置信息。其过程包括图像处理和文字识别。本文提出的方法是:在图像处理过程中,首先利用颜色的彩色空间变换,分割出棋局区域图像。之后细分图像,将棋局分割成子图像,对每个子图像进行棋子存在及颜色判断。对棋子进行阈值粗分割及形态学细化处理,采用霍夫变换检测棋子外圈,得到棋子精确定位后对棋子再次阈值分割,最终得到棋子中的文字图像。在文字识别过程中,提取棋子文字旋转不变的径向像素点数特征,用BP神经网络进行识别,并采用贝叶斯正则化方法提高网络的推广性。基本步骤包括棋局区域分割、棋子粗分割、棋子细分割、棋子的汉字特征提取和识别等,如图1所示。

1　棋局区域分割

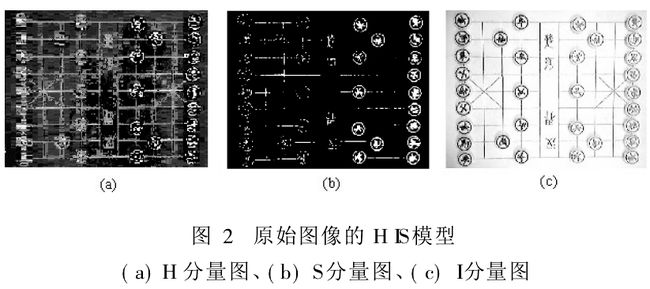
原始棋局图像由CCD摄像头在棋盘正上方拍摄所得, 24位真彩色, 640像素×480像素。原始棋局图像超出了棋局的范围,工作的第一步是要把棋局区域从图像中分割出来。对于彩色图像,如何充分利用彩色信息进行图像分割是工作的重点。在彩色图像处理中,最常用的颜色模型是HIS模型它比较适于描述人类的彩色感觉。将原始图像由RGB模型转换为HIS模型,可以分别得到H(色调)、S(饱和度)、I(亮度)分量图,如图2所示。从S分量图可以看出,棋局区域(包括棋子和棋盘上的线条)与棋局外的台面部分的饱和度具有明显的区别。因此可以简单地用一个阈值把棋局区域和台面分割开来。

2　棋子分割

将棋局区域分割出来后,下一步的工作是将棋局中的每个棋子分别分割出来。在这一步中我们仍然要利用图像的彩色信息。

2.1　棋盘细分

注意到图像在亮度上的不均衡性,采用了一种细分的子图像分割方法。首先对应棋子的可能位置,将整个棋盘切割成9×10个方形的子图像,即粗略定位后的棋子图像。每个子图像的中心为棋盘上线与线的交叉点,这些交叉点是棋子应该放置的位置;边长取值略大于棋子的直径(这样可以适应棋子位置稍为偏斜的情况)。

2.2　棋子存在及颜色判断

接下来是判断每个子图像中是否含有棋子。观察棋局的I分量图可知,黑棋相对于图像的其他部分具有明显偏低的I分量。因此,首先利用I分量信息判断每个子图像中是否含有黑棋。对于任意子图像,用特定阈值分割其I分量图,计算分割后的二值图像的黑色像素数,如果大于某个设定的阈值,则判定此子图像含有黑棋。对于不存在黑子的子图像,则进一步判断它是否含有红棋。此时利用S分量信息,用类似于判断黑子的方法可以得到正确的结果。

2.3　棋子粗分割

接下来,需要从含有棋子的子图像中分割出棋子来。对于黑子,我们利用亮度信息进行分割。在含有黑子的子图像中,首先进行阈值分割,如图3所示。经过这样分割得到的二值图像还含有由于棋盘上线条和其他原因形成的噪声信息,因此把这一次分割称为粗分割。对于红子,我们则利用饱和度信息进行分割,可得到类似黑棋的结果。

2.4　棋子细分割

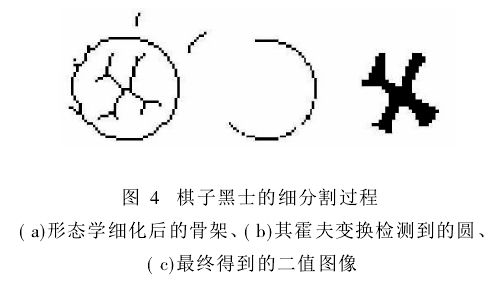
从前面的粗分割得到的图像中含有一定的噪声,而这些噪声基本都位于棋子的范围之外。如果能对棋子精确定位,仅切割出棋子范围内的图像,就可以去除棋子外的噪声。注意到每个棋子的边缘都有一个圆圈,这个圆圈可以确定棋子的范围和位置。如果知道了该圆的半径和圆心,就可以对棋子精确定位。

从图像中检测圆的一个有效方法是霍夫(Hough)变换。首先对前面粗分割后得到的二值子图像运用形态学细化的方法,得到原图的骨架。之后用霍夫变换检测出子图像中的圆,同时得到圆的圆心和直径。以圆心的位置对每个棋子进行重定位,切割出包含仅棋子的子图像,此时得到的子图像称为精确定位棋子图像。最后用Ostu方法[3]自动选取阈值,对子图像进行阈值分割,得到仅含文字的子图像。最终得到的文字图像是27×27像素的黑白图像。图4显示了这一过程。

3　棋子识别

前面一系列图像处理的工作,目的是为了从原图中提取出要识别的目标———汉字。对汉字的识别技术已经比较成熟[4,5],但对中国象棋的识别,与一般的汉字识别有所不同。因为这里需要识别的汉字种类很少,对中国象棋来说,只需识别车,马,砲(黑棋),炮(红棋),象(黑棋),相(红棋),士(黑棋),仕(红棋),将,帅,卒,兵12种不同的汉字。所以采用的是与一般汉字识别不同的方法。

3.1　特征提取

为了正确的识别,文字特征的提取至关重要。在下中国象棋时,棋子可以任意旋转地放置。因此必须要克服由于旋转造成的识别困难。为此须提取图像旋转不变的特征进行识别。我们首先尝试提取具有旋转不变特性的图像的Hu矩和Zernike矩特征[6]。在对各棋子图像进行位置和尺度归一化之后,分别计算其Hu矩的7个不变矩特征和Zernike矩的前四阶矩特征,取对数后作为输入,用BP神经网络分别进行训练,但是结果表明,无论是Hu矩还是Zernike矩,都难以达到较高的识别率(均低于80% )。分析其原因在于,由于摄像头本身性能和灯光等环境因素的影响,使摄像头每次拍摄的棋局图像存在差别,导致最终分割出的同类的棋子图像间也存在汉字笔画粗细、模糊程度的不同。此外,也存在图像数字化和噪声带来的误差影响。这使得同类棋子计算出的矩不变量存在较大的差别,从而造成了识别率的降低。经过对棋子图像的分析,我们发现图像的径向像素点数特征可以很好地反应某个汉字的结构特征,并且对其归一化后它对汉字笔画的粗细以及噪声的影响不敏感,此外,它还是旋转不变的。因此,我们提取图像的径向像素点数作为特征。具体做法是:

1)平移图像。使各棋子图像的矩心坐标与矩形中心坐标重合。即作变换:

f1(x1,y1)=f(x+x,y+y),这里(x,y)是图像的矩心坐标。

2)以图像中心为原点,以等间隔半径作多个圆,计算位于相邻两圆间的文字像素点数Countj, (1≤j≤n)。n这里取13。这样对每个棋子,都得到一个13维的像素点数向量Count。

3)将像素点数进行归一化处理。即对每个棋子的像素点数向量Count作归一化处理得到13维的特征向量P,其各维分量为:

3.2　特征识别

神经网络是进行模式识别的常用方法。本文采用包含一个隐藏层的BP神经网络,隐含层和输出均采用对数S型激励函数。样本集为{Pi,Ti},1≤i≤1920。输入Pi为13维的特征向量。Ti为12维的目标向量,对应12种棋子。经过实验比较,确定网络结构为13-20-12,采用Levenberg-Marquardt算法[7]进行训练。用前960个样本作为训练集,后960个样本作为测试集。以随机的权值初始化网络,进行5次训练。结果训练集的平均正确率为96.5%,测试集的平均错误率为85.7%。可见网络的推广能力一般,识别率不高,有待改进。

3.2.1　贝叶斯正则化方法

如何提高神经网络的推广能力一直受到广泛关注。David Mackay提出了用统计学中的贝叶斯理论来优化调整神经网络以获得良好推广能力的方法[8]。通常一个BP网络的训练目标是减少总平方误差:F=E_D。其中

,n为样本数量, ti是第i个样本的期望输出, ai为网络的实际输出。而贝叶斯正则化方法的训练目标则是:F=βED+αEW。其中,

表示权值的平方和,N为权值总数。α和β是目标函数的参数。权值越小,网络的推广能力越强。如果α<<β,则训练注重于使训练集的误差最小,但是难以获得很好的推广性;如果α>>β,则训练注重于提高网络的推广性,但是训练集误差将不能保证最小,网络输出更加平滑。通过采用新的目标函数,可以在保证网络训练误差尽可能小的情况下使网络具有较小的权值,相当于缩小了网络的规模。

按照贝叶斯理论,求权值W的最优值即求W的后验概率P(W|D,α,β,M)的最大值,其中D表示样本集,M表示使用的特定网络结构。而这等价于求目标函数F(W)=βED+αEW的最小值。Mackay经推导得到目标函数的参数α、β分别为:

这里

是目标函数的海森矩阵。γ称作有效权值数,取值范围0~N。它衡量一个BP网络中真正有效的权值的个数。如果网络训练最终得到的γ值接近N,则表示现在的网络结构还不够复杂,可以再增加神经元数目;如果增加了网络的复杂度,但γ值基本保持不变,就可认为前面的网络已可以满足要求。

3.2.2　实验结果与分析

Foresee和Hagan采用贝叶斯正则化方法,利用高斯牛顿法近似计算海森矩阵,并利用Levenberg-Marquardt算法对BP网络进行训练[9]。我们在实验中采用同样的算法,对隐含层神经元数S取不同的值进行训练,表1是训练的结果。

可见,随着S的增大,ED、EW逐渐减小,而γ值逐渐增大。但是S在达到20以后,γ值基本保持不变,说明网络已经足够复杂,S取值不需要增加了;相应的,此时ED的值也已经收敛。S=20时,训练集的正确率为99.9%,测试集的正确率也达到了93.1%。与前面不用贝叶斯正则法的训练相比,训练集和测试集的正确率都有了提高,网络的推广能力的增强相当可观。从实验结果也可看出,用图像的径向像素点数特征对棋子图像进行识别,具有比用Hu矩和Zernike矩更好的效果。

4　结束语

基于视觉的仿人对弈机器人在国内尚无先例,其关键在于其视觉系统中的图像处理和识别。本文提出了基于彩色图像的,应用阈值分割、形态学细化、霍夫变换等图像处理技术对机器人视觉图像进行分割、提取出棋子图像的方法。在对棋子的识别中,与一般汉字特征提取方法不同,提取了具有旋转不变性的像素径向分布点数的特征。在用神经网络进行训练识别时,引入了贝叶斯正则化方法对网络训练进行优化,最终棋子识别率达到了93. 1%。通过与传统BP神经网络训练方法的比较,证明了贝叶斯正则法在增强网络推广性和提高整体识别率上有明显的优势。实验结果也表明用图像的径向像素点数特征对棋子图像进行识别,具有比用Hu矩和Zernike矩更好的效果。

参考文献

[ 1 ]高志华,沈小丽.智能中国象棋棋盘的开发[J].中国计量学院学报, 2001, 12(1): 91-94.

[ 2 ]黄力波,夏庭锴,王春香,等.实时环境下的对弈机器人控制系统设计与分析[J].机械, 2004, 31(6): 50-52.

[ 3 ] Ostu N.A threshold selection methodfrom gray-level histogram [J].IEEE Trans SystemsMan Cybernetic, 1978(8): 62-65.

[ 4 ]郭戈,闫继宏,蒋红梅,等.基于结构特征的汉字识别[J].甘肃工业大学学报, 2003, 29(1): 81-85.

[ 5 ]汪芳,康慕宁,李先国.印刷体汉字识别技术[J].情报技术, 2004(2): 32-33.

[ 6 ]丁兴号,邓善熙.Hu矩和Zernike矩在字符识别中的应用[J].工具技术, 2003, 37: 16-18.

[ 7 ] Martin THagan,Mohammad B Menha.jTraining feedforward networks with theMarquardt algorithm [J]. IEEETransactions on NeuralNet- works, 1994, 5(6): 989-993.

[ 8 ] D JCMackay. BayesianInterpolation[J].NeuralComputation, 1992,4: 415-447.

[ 9 ] FDan Foresee,MartinTHagan.Gauss-Newtonapproximation toBayes-ian Learning[ J]. IEEE Transactions on Neural Networks,1997, 3:1930-1935.