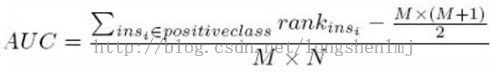ROC曲线的AUC（以及其他评价指标的简介）知识整理

相关评价指标在这片文章里有很好介绍

信息检索（IR）的评价指标介绍 - 准确率、召回率、F1、mAP、ROC、AUC:http://blog.csdn.net/marising/article/details/6543943

ROC曲线：接收者操作特征（receiveroperating characteristic）

比较分类模型的可视工具，曲线上各点反映着对同一信号刺激的感受性。

纵轴：真正率（击中率）true positive rate ,TPR，称为灵敏度。所有实际正例中，正确识别的正例比例。TPR=TP/ (TP+FN)

横轴：假正率（虚报率）false positiverate, FPR，称为特异度。所有实际负例中，错误得识别为正例的负例比例。FPR= FP / (FP + TN)

 

 

		Pos	neg
	Pos	True positive(TP)	False positive(FP)		Predicted Positive(P’=TP+FP)
	neg	False negative(FN)	True negative(TN)		Predicted Negative(N’=FN+TN)
		Actual pos(P=TP+FN)	Actual neg(N=FP+TN)

 

P为所有正例个数

N为所有负例个数。

TPR=TP/ (TP+FN) = TP/P

FPR=FP / (FP +TN)= FP/N

 

 

	Pos	Neg
pos	TP=70	FP=30	P’=100
neg	FN=20	TN=80	N’=100
	P=90	N=110

 

则相关数值请自己计算。

 

 

一个阈值就决定了ROC空间中点的位置。举例来说，如果可能值低于或者等于0.8这个阈值就将其认为是正类，而其他的值被认为是负类。这样就可以通过画每一个阈值的ROC点来生成一个生成一条曲线。MedCalc是较好的ROC曲线分析软件。

在ROC空间坐标中，左上角的点，轴(0,1)点，这个代表着100%灵敏（没有假阴性）和100%特异（没有假阳性）。而(0,1)点被称为完美分类器。

而副对角线，也就是从左下到右上的对角线，也叫无识别率线，代表着一个完全随机预测。一个最直观的随机预测的例子就是抛硬币。

Roc曲线用来评价分类器的性能。通过测试分类结果可以计算得到TPR和FPR的一个点对。再通过调整这个分类器分类的阈值（从0.1到0.9），阈值的设定将实例分类到正类或者负类（比如大于阈值划分为正类）。因此根据变化阈值会产生不同效果的分类，得到多个分类结果的点，可以画出一条曲线，经过(0, 0)，(1, 1)。

 

曲线在对角线左上方，离得越远说明分类效果好。如果出现在对角线右下方，直观的补救办法就是把所有的预测结果反向，即：分类器目的是识别正例，但效果差，所以把分类器输出结果正负颠倒，把输出的正例当成负例，把负例当成正例。就得到一个好的分类器。从源头上说，分类器越差越好。

因为研究分类器阈值的指定，所以，ROC曲线还可以用来计算“均值平均精度”（mean average precision），这是当你通过改变阈值来选择最好的结果时所得到的平均精度（PPV）.

另外，在一些分类问题中犯不同的错误代价是不同的(cost sensitive learning)。这样，默认0.5为分类阈值的传统做法也显得不恰当了。在我的代价敏感学习的研究论文Cost-sensitive Decision Tree for Uncertain Data探讨了代价的衡量问题。制定cost的标准受行业限制，比如医疗机构，误诊以后，癌症病人直接导致病人死亡，这很难用cost衡量。而测试的项目很容易用金钱衡量。

所以分类的阈值的选定，本身就是一个研究课题。收到分类器以及数据对象的限制。普通数据，可以用0.5分类，而其他的情况下阈值的选择需要实际测试矫正。

而cost sensitive 直接定义一个cost作为分类标准，这个权重的指定包含原有的概率，还涉及实际产生的代价，从而叠加到一起作为分类标准。

如果在特定行业内，指定标准合理，会有很大的帮助。比如信用卡欺诈识别。

 

 

而曲线ROC curve右下方的面积成为Area Under roc Curve(AUC) 值介于0.5到1.0之间，较大的AUC代表了较好的performance

 

引用一个百度里的例子：

下表是一个逻辑回归得到的结果。将得到的实数值按大到小划分成10个个数相同的部分。

Percentile	实例数	正例数	1-特异度(%)	敏感度(%)
10	6180	4879	2.73	34.64
20	6180	2804	9.80	54.55
30	6180	2165	18.22	69.92
40	6180	1506	28.01	80.62
50	6180	987	38.90	87.62
60	6180	529	50.74	91.38
70	6180	365	62.93	93.97
80	6180	294	75.26	96.06
90	6180	297	87.59	98.17
100	6177	258	100.00	100.00

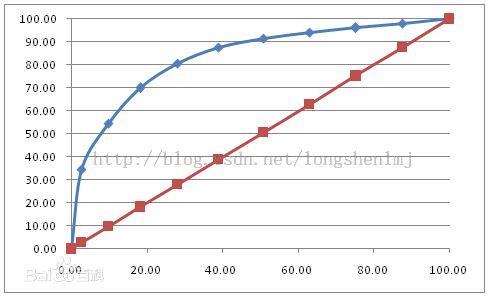
其正例数为实际的正类数。就是说，将逻辑回归得到的结果按从大到小排列，倘若以前10%的数值作为阈值，即将有10%的实例都划归为正类，6180个。其中，正确的个数为4879个，占所有正类的4879/14084*100%=34.64%，即敏感度；另外，有6180-4879=1301个负实例被错划为正类，占所有负类的1301 /47713*100%=2.73%,即特异度。以这两组值分别作为x值和y值，在excel中作散点图。得到ROC曲线如下

 

AUC的计算方法总结：

1．直接计算曲线下的梯形面积

最直观的，根据AUC这个名称，我们知道，计算出ROC曲线下面的面积，就是AUC的值。事实上，这也是在早期Machine Learning文献中常见的AUC计算方法。由于我们的测试样本是有限的。我们得到的AUC曲线必然是一个阶梯状的。因此，计算的AUC也就是这些阶梯下面的面积之和。这样，我们先把score排序(假设score越大，此样本属于正类的概率越大)，然后一边扫描就可以得到我们想要的AUC。但是，这么做有个缺点，就是当多个测试样本的score相等的时候，我们调整一下阈值，得到的不是曲线一个阶梯往上或者往右的延展，而是斜着向上形成一个梯形。此时，我们就需要计算这个梯形的面积。由此，我们可以看到，用这种方法计算AUC实际上是比较麻烦的。

2．给定所有正负样本的得分score，组成正负样本对，利用正样本大于负样本所出现的频率（也可以说是个数）来计算AUC。

一个关于AUC的很有趣的性质是，它和Wilcoxon-Mann-WitneyTest是等价的。而Wilcoxon-Mann-WitneyTest就是测试任意给一个正类样本和一个负类样本，正类样本的score有多大的概率大于负类样本的score。有了这个定义，我们就得到了另外一种计算AUC的办法：得到这个概率。我们知道，在有限样本中我们常用的得到概率的办法就是通过频率来估计之。这种估计随着样本规模的扩大而逐渐逼近真实值。这和上面的方法中，样本数越多，计算的AUC越准确类似，也和计算积分的时候，小区间划分的越细，计算的越准确是同样的道理。具体来说就是统计一下所有的MXN(M为正类样本的数目，N为负类样本的数目)个正负样本对中，有多少个组中的正样本的score大于负样本的score。当二元组中正负样本的score相等的时候，按照0.5计算。然后除以MN。实现这个方法的复杂度为O(n^2)。n为样本数（即n=M+N）。

3．按样本score排序，按排序数计算正样本大于负样本的个数，来计算AUC

第三种方法实际上和上述第二种方法是一样的，但是复杂度减小了。它也是首先对score从大到小排序，然后令最大score对应的sample的rank为n，第二大score对应sample的rank为n-1，以此类推。然后把所有的正类样本的rank相加，再减去正类样本的score为最小的那M个值的情况。得到的就是所有的样本中有多少对正类样本的score大于负类样本的score。然后再除以MXN。

 

另外，特别需要注意的是，当存在score相等的情况时，对相等score的样本，需要赋予相同的rank(无论这个相等的score是出现在同类样本还是不同类的样本之间，都需要这样处理)。具体操作就是再把所有这些score相等的样本的rank取平均。然后再使用上述公式。

 

 

此外，还有其他评价指标：

F1-Measure

F1-Measurea评价指标经常在信息检索和自然语言处理中使用。是根据准确率Precision和召回率Recall二者给出的一个综合的评价指标，具体定义如下：

F1 = 2rp / ( r+p )

其中r为recall，p为precision.

另外还以一些学术里，经常用到的指标，其定义的表达式如下

给出网络上的一个例子：

以下部分内容引致网络

ROC曲线

得此名的原因在于曲线上各点反映着相同的感受性，它们都是对同一信号刺激的反应，只不过是在几种不同的判定标准下所得的结果而已。接受者操作特性曲线就是以虚报概率为横轴，击中概率为纵轴所组成的坐标图，和被试在特定刺激条件下由于采用不同的判断标准得出的不同结果画出的曲线。

最好的可能预测方式是一个在左上角的点，在ROC空间坐标轴(0,1)点，这个代表着100%灵敏（没有假阴性）和100%特异（没有假阳性）。而(0,1)点被称为完美分类器。一个完全随机预测会得到一条从左下到右上对角线（也叫无识别率线）上的一个点。一个最直观的随机预测的作决定的例子就是抛硬币。 

这条斜线将ROC空间划分为两个区域，在这条线的以上的点代表了一个好的分类结果,而在这条线以下的点代表了差的分类结果。

图中给出了上面4个结果的ROC空间分布。A方式的结果是A,B,C中最好的一个。B的结果是一种随机猜测线（那条斜线），在表中我们可以看到B的精确度是50%。然而当将C作一个镜像后，C的结果甚至要比A还要好。这个作镜像的方法就是简单的不管C预测了什么，就做其预测的反面。离左上角越近的预测，其结果越好。或者说，离随机猜测线越远，则预测的结果越好，如果其点是在右下方的，那么只需作一个镜像即可。

ROC空间中的线

离散分类器，如决策树，产生的是离散的数值或者一个双标签。应用到实例中，这样的分类器最后只会在ROC空间产生单一的点。而一些其他的分类器，如朴素贝叶斯分类器，逻辑回归或者人工神经网络，产生的是实例属于某一类的可能性，对于这些方法，一个阈值就决定了ROC空间中点的位置。举例来说，如果可能值低于或者等于0.8这个阈值就将其认为是阳性的类，而其他的值被认为是阴性类。这样就可以通过画每一个阈值的ROC点来生成一个生成一条曲线。MedCalc是较好的ROC曲线分析软件。

 

Area Under roc Curve(AUC)就出现了。AUC的值就是处于ROCcurve下方的那部分面积的大小。通常，AUC的值介于0.5到1.0之间，较大的AUC代表了较好的performance。

AUC是一种用来度量分类模型好坏的一个标准。这样的标准其实有很多，例如：大约10年前在machine learning文献中一统天下的标准：分类精度；在信息检索(IR)领域中常用的recall和precision，等等。其实，度量反应了人们对“好”的分类结果的追求，同一时期的不同的度量反映了人们对什么是“好”；这个最根本问题的不同认识，而不同时期流行的度量则反映了人们认识事物的深度的变化。近年来，随着machine learning的相关技术从实验室走向实际应用，一些实际的问题对度量标准提出了新的需求。特别的，现实中样本在不同类别上的不均衡分布(class distribution imbalance problem)。使得accuracy这样的传统的度量标准不能恰当的反应分类器的performance。举个例子：测试样本中有A类样本90个，B 类样本10个。分类器C1把所有的测试样本都分成了A类，分类器C2把A类的90个样本分对了70个，B类的10个样本分对了5个。则C1的分类精度为 90%，C2的分类精度为75%。但是，显然C2更有用些。另外，在一些分类问题中犯不同的错误代价是不同的(cost sensitive learning)。这样，默认0.5为分类阈值的传统做法也显得不恰当了。

为了解决上述问题，人们从医疗分析领域引入了一种新的分类模型performance评判方法——ROC分析。ROC分析本身就是一个很丰富的内容，有兴趣的读者可以自行Google。由于我自己对ROC分析的内容了解还不深刻，所以这里只做些简单的概念性的介绍。