floyd-warshall 算法分析 每对顶点之间的最短路
floyd 算法是基于DP(动态规划的一种算法),用于求每对顶点之间的最短路。
floyd 算法是 三层 for 循环 ,复杂度是O(v^3) ,并且 隐藏在 O(v^3)下的常数也是非常小
算法介绍:
- 它需要用邻接矩阵来储存边
- 从任意一条单边路径开始。所有两点之间的距离是边的权,如果两点之间没有边相连,边权就是无穷大。
- 对于每一对顶点 u 和 v,看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短。如果是更新它。这种方法做松弛技术。松弛技术是三角关系 实质就是 : d(s,u)= min(d(s,u), d(s,v)+d(v,u) ) 。d(s,u) 表示从s点到 u 点的路径长度。。。也就是如果找到一条比当前路径更短的路径长度,就更新当前的路径长度。。
这个算法通过考虑最佳子路径来得到最佳路径。这个算法很容易实现,只要几行。
dp状态转移的方程是 : dp[k,i,j]=min(dp[k-1,i,j],dp[k-1,i,k]+dp[k-1,k,j])
for(int k =1 ; k <= n ; k ++ ){
for(int i =1 ; i<= n ; i++){
for(int j =1 ;j<=n;j++){
dp[k][ i ][ j ]= min( dp[k-1][ i ][ j ],dp[k-1][ i ][ k ]+dp[k-1][ k ][ j ] );
}
}
}
其实三维的空间是没必要的,因为每次都是有前一种状态跟新过来的,因此用二维的dp[ i ][ j ]即可,二维滚动数组,好比 二维0-1 背包转化为 一维的思路。
于是代码就可以写成 :
二维:
for(int k =1 ; k <= n ; k ++ ){
for(int i =1 ; i<= n ; i++){
for(int j =1 ;j<=n;j++){
dp[ i ][ j ]= min( dp[ i ][ j ],dp[ i ][ k ]+dp[ k ][ j ] );
}
}
}
从DP 方向来分析这个很神奇的算法:
最先应该搞懂的就是 最有子结构是什么??
首先应该是对所有的点进行标号. 从1 标号到 n ,每个点都有一个标号。。dp[ i ][ j ] 代表的就是 标号为 i 的点和 标号为 j 的点的路径长度。。
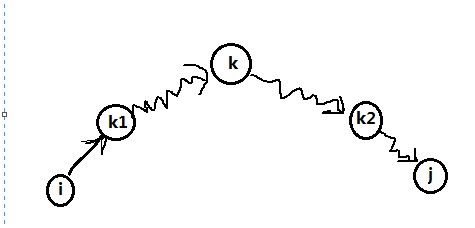
应该从三维来思考这个问题, dp[ k , i , j ] 代表着 从顶点 i 到顶点 j ,且满足所有中间顶点都属于 集合{1,2,3,4,......,k}的一条最短路径的权值。。也就是 从顶点 i 到 顶点 j 所有的路径 的中间节点的最大值为k。
分析: 中间顶点 是指 路径 从i 到 j ,中间经过点是 这条路径的 中间节点 。
比如 8-->5-->4-->9-->1-->3-->6
对于 8 --》6 这条路径 的中间节点是 5,4,9,1,3
对于5 --》 1 这条路径的中间节点 是 4,9
给出一个思维过程 : 逆向来推的话 就可以用归纳推理 来证明。。
有这样一个性质 第一层循环从1到 k 时候, 所有 中间节点都小于 k 的路径 ,都已经 是最小路径长度, 也就是 都已经是最优解了。。 也就是 如果 i -->j 所有的路径的中间节点 都小于 K的 话, 计算到 k时 ,dp[k][ i ][ j ] 所表示的值已经是 i-->j 的最优值了。。
在这个图中 ,i --》 j 中 当 k 是这条路径上的 标号最大的点的时候 : dp[ k -1][ i ][ k ]就是从 i--》 k的最短路的路径长度,同时k--》 j 的路径dp[k -1][ i ][ j ] 也已经存储的是最优解了 。 (证明 : )
由于 k 是 路径 i--》j 上 标号最大的点 ,所以在 i--》k 最优解的路径(说的是 从 i--> k 的最短路径的那一条)上 ,如果存在中间点的时候,中间点中定存在一个最大值k1, k1 一定小于k,所以在计算 k1的时候 就已经 把 i--》 k 的最短路径长度求出来了,也就是dp[ k1][ i ][ k ]存储的就是最小值。如果 i--> k 的最短的路径上 i 和 k 直接相连,那么dp[0][ i ][ k ]也一定是最短路径了。(dp[0][ i ][ j ]表示直接相连的点的路径长度,并不是从最短路径,只是相连的那条边的长度),由性质2得,dp[k-1][ i ][ k ]存储的就是从i-->k 路径长度的最小值了。同理 k--j 这条路径上的因此dp[k-1][ k ][ j ]最短路径长度也求出来了。。
因此 i--> k 以及 k--> j 存储的都已经是最小值了。
所以 dp[k][ i ][ j ]= min( dp[k-1][ i ][ j ],dp[k-1][ i ][ k ]+dp[k-1][ k ][ j ] ) ;
经过这个松弛操作后 dp[k][ i ][ j ] 就是 从 i 到 j 所有路径中的最小路径长度了。。
性质2:在以后的操作 总满足 dp[ k+1][ i ][ j ] = dp[ k ][ i ] [ j ]; 因为 i-->j 的路径上 不包含 k+1。
因为: 路径中间节点的最大值为k的那些路径,总可以 由 中间节点的最大值 小于k 的那些路径 经过松弛操作求出。
最有子结构就很显然了: 就是中间节点的最大值的 比k小的 那些路径。。
无后效性 很容易得知。。
因此满足了 DP的条件 ,因此 用DP 来求任意两点之间的最短路径长度的 floyd 的算法 是正确的 。。
在应用是 应该将 三维 数组 换成二维数组 来求解 (三维是便于理解)
经常有这么一个问题 为什么 k 的循环放在最外层?? 其实答案很简单 因为 dp[ k ][ i ][ j ] 是有 dp[ k-1 ][ i ][ j ] 也就是 dp[ k ] 这个矩阵是由 dp[ k-1 ] 这个矩阵求得的。。。