K-means学习笔记
K-means聚类算法 由J. MacQueen1967年提出，然后通过 J. A. Hartigan 和 M. A. Wong 在1975年进一步推广。简单的说，K-means算法是指将基于特征表示的数据分成K组的算法。该方法是通过最小化每一个数据和对应簇集中心数据的距离之和来进行分组。K-means的目的是使数据集的数据得到分组。
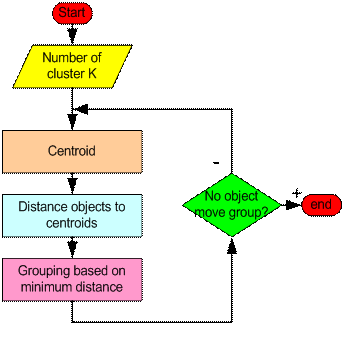
K-mean基本步骤是很简单的：
首先，我们来决定K的大小以及设定K个初始的聚类中心。我们可以随机选取初始聚类中心也可以按顺序取前K个值作为聚类中心。
然后，K-means将重复下面3个步骤直到收敛。
迭代到稳定（即最优函数不在变化）
1.确定新的聚类中心
2.计算每一个数据点到聚类中心的距离。
3.依据最小距离对其分组，分到对应的距离最小的簇集中心所在的位置
最后，数据点所在组不再发生（我认为和聚类中心不变是一个意思）变化停止迭代分类结束。
Examples：
Suppose we have several objects (4 types of medicines) and each object have two attributes or features as shown in table below. Our goal is to group these objects into K=2 group of medicine based on the two features (pH and weight index).
| Object |
attribute 1 (X): weight index |
attribute 2 (Y): pH |
| Medicine A |
1 |
1 |
| Medicine B |
2 |
1 |
| Medicine C |
4 |
3 |
| Medicine D |
5 |
4 |
Each medicine represents one point with two attributes (X, Y) that we can represent it as coordinate in an attribute space as shown in the figure below.
1. Initial value of centroids : Suppose we use medicine A and medicine B as the first centroids. Letanddenote the coordinate of the centroids, then
and
2. Objects-Centroids distance : we calculate the distance between cluster centroid to each object. Let us useEuclidean distance, then we have distance matrix at iteration 0 is
Each column in the distance matrix symbolizes the object. The first row of the distance matrix corresponds to the distance of each object to the first centroid and the second row is the distance of each object to the second centroid. For example, distance from medicine C = (4, 3) to the first centroid is, and its distance to the second centroid
is, etc.
3. Objects clustering : We assign each object based on the minimum distance. Thus, medicine A is assigned to group 1, medicine B to group 2, medicine C to group 2 and medicine D to group 2. The element of Group matrix below is 1 if and only if the object is assigned to that group.
4. Iteration-1, determine centroids : Knowing the members of each group, now we compute the new centroid of each group based on these new memberships. Group 1 only has one member thus the centroid remains in
. Group 2 now has three members, thus the centroid is the average coordinate among the three members:
.
5. Iteration-1, Objects-Centroids distances : The next step is to compute the distance of all objects to the new centroids. Similar to step 2, we have distance matrix at iteration 1 is
6. Iteration-1, Objects clustering: Similar to step 3, we assign each object based on the minimum distance. Based on the new distance matrix, we move the medicine B to Group 1 while all the other objects remain. The Group matrix is shown below
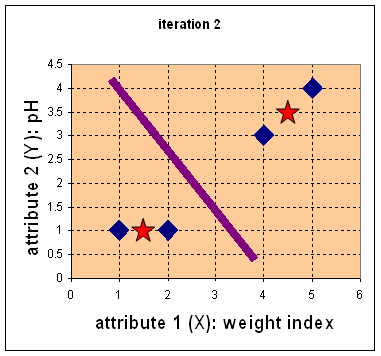
7. Iteration 2, determine centroids: Now we repeat step 4 to calculate the new centroids coordinate based on the clustering of previous iteration. Group1 and group 2 both has two members, thus the new centroids are
and
8. Iteration-2, Objects-Centroids distances : Repeat step 2 again, we have new distance matrix at iteration 2 as
9. Iteration-2, Objects clustering: Again, we assign each object based on the minimum distance.
We obtain result that . Comparing the grouping of last iteration and this iteration reveals that the objects does not move group anymore. Thus, the computation of the k-mean clustering has reached its stability and no more iteration is needed. We get the final grouping as the results
| Object |
Feature 1 (X): weight index |
Feature 2 (Y): pH |
Group (result) |
| Medicine A |
1 |
1 |
1 |
| Medicine B |
2 |
1 |
1 |
| Medicine C |
4 |
3 |
2 |
| Medicine D |
5 |
4 |
2 |