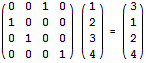hdu2371之矩阵快速幂

Decode the Strings

Time Limit: 1000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 537    Accepted Submission(s): 167

Problem Description

Bruce Force has had an interesting idea how to encode strings. The following is the description of how the encoding is done: 

Let x ₁,x ₂,...,x _n be the sequence of characters of the string to be encoded. 

1. Choose an integer m and n pairwise distinct numbers p ₁,p ₂,...,p _n from the set {1, 2, ..., n} (a permutation of the numbers 1 to n). 
2. Repeat the following step m times. 
3. For 1 ≤ i ≤ n set y _i to x _pi, and then for 1 ≤ i ≤ n replace x _i by y _i. 

For example, when we want to encode the string "hello", and we choose the value m = 3 and the permutation 2, 3, 1, 5, 4, the data would be encoded in 3 steps: "hello" -> "elhol" -> "lhelo" -> "helol". 

Bruce gives you the encoded strings, and the numbers m and p ₁, ..., p _n used to encode these strings. He claims that because he used huge numbers m for encoding, you will need a lot of time to decode the strings. Can you disprove this claim by quickly decoding the strings? 

 

Input

The input contains several test cases. Each test case starts with a line containing two numbers n and m (1 ≤ n ≤ 80, 1 ≤ m ≤ 10 ⁹). The following line consists of n pairwise different numbers p ₁,...,p _n (1 ≤ p _i ≤ n). The third line of each test case consists of exactly n characters, and represent the encoded string. The last test case is followed by a line containing two zeros. 

 

Output

For each test case, print one line with the decoded string. 

 

Sample Input

   
   
   
   

    
    
    
    5 3
2 3 1 5 4
helol
16 804289384
13 10 2 7 8 1 16 12 15 6 5 14 3 4 11 9
scssoet tcaede n
8 12
5 3 4 2 1 8 6 7
encoded?
0 0
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    hello
second test case
encoded?
   
   
   
   
   
   
   
   


   
   
   
   
   
   
   
   

    
    
    
    题目意思是给出n个字符的置换方式,经过m次转换后得到了最终字符串(就是给定的字符串),求最初的字符串
   
   
   
   
   
   
   
   

    
    
    
    分析:假定最初字符串序号是1,2,3,4,置换方式是3,1,2,4，即1,2,3,4置换一次后得到3,1,2,4构成的字符串
   
   
   
   
   
   
   
   

    
    
    
     将1 2 3 4置换为3 1 2 4，相当于下面的矩阵乘法：
    
    
    
    

    
    
    
         
    
    
    
    
   
   
   
   
   
   
   
   

    
    
    
    如果置换m次则将置换矩阵*m次即可，最后乘上给定的字符串矩阵得到最终字符串矩阵(就是得到的矩阵第i行第j列是1表示由s[j]得到第s[i]个字符)
   
   
   
   
   
   
   
   

    
    
    
    但是本题是给定结果，叫我们求最初的矩阵，其实就是将原来矩阵求逆矩阵的m次
   
   
   
   
   
   
   
   

    
    
    
    A*B^m=C =>A=C*B^(-m),
   
   
   
   
   
   
   
   

    
    
    
    A*A^-1=I;//I是单位矩阵
   
   
   
   
   
   
   
   

    
    
    
    注意到这里的矩阵A元素为0或1且每一行每一列只有一个1，则A中的A[i][k]*B[k][j]=I[i][j]=1,i == j,所以A的逆矩阵就是A逆s[i][j]=A的s[j][i]
   
   
   
   
   
   
   
   

    
    
    
    
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<queue>
#include<algorithm>
#include<map>
#include<iomanip>
#define INF 99999999
using namespace std;

const int MAX=80+10;
int array[MAX][MAX],sum[MAX][MAX];
char s[MAX];
int n,m,a;

void MatrixMult(int a[MAX][MAX],int b[MAX][MAX]){
	int c[MAX][MAX]={0};
	for(int i=0;i<n;++i){
		for(int j=0;j<n;++j){
			for(int k=0;k<n;++k){
				c[i][j]+=a[i][k]*b[k][j];
			}
		}
	}
	for(int i=0;i<n;++i){
		for(int j=0;j<n;++j)a[i][j]=c[i][j];
	}
}

void MatrixPow(int k){
	for(int i=0;i<n;++i){
		for(int j=0;j<n;++j){
			sum[i][j]=(i == j);
		}
	}
	while(k){
		if(k&1)MatrixMult(sum,array);
		MatrixMult(array,array);
		k>>=1;
	}
}

int main(){
	while(cin>>n>>m,n+m){
		memset(array,0,sizeof array);
		for(int i=0;i<n;++i){
			cin>>a;
			array[a-1][i]=1;//初始矩阵 
		}
		getchar();
		gets(s);
		MatrixPow(m);//置换m次
		for(int i=0;i<n;++i){
			for(int j=0;j<n;++j){
				if(sum[i][j]){printf("%c",s[j]);break;}
			}
		}
		cout<<endl;
	}
	return 0;
}