解决U-turn问题的Dijkstra算法（基于实际道路交通网络）

算法介绍

Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。主要特点是从始点S向外迭代，每次迭代产生当前最短路径，当迭代至终点E时算法结束。

该算法需要设置两个集合，临时标记的节点集合OpenedList和最终标记的节点集合SettledList。OpenedList集合中记录当前访问到的节点（即当前可见节点），SettledList中记录已经求出最短路径的节点。算法基本过程如下：

1、初始化OpenedList集合为与起始节点S直接相临接的节点T1，T2……Tn。SettledList初始化为起始节点S。

2、判断OpenedList集合是否为空，若为空则说明找不到一条从S到E的最短路径，算法退出。否则从OpenedList集合中取出距离S最近的节点SettledNode，并将SettledNode加入SettledList集合，判断SettledNode是否是终点E，如果是则转4，如果不是终点，转3。

3、读取和SettledNode直接相临接的节点T1'，T2'……Tn'，判断Ti'是否在OpenedList集合中，a.若在，则判断S距离Ti'的距离newMinDistance是否小于原有的MinDistance，若是，则更新S到Ti'的最短距离为newMinDistance;b.若不在，将Ti'加入到OpenedList集合中，转2。

4、输出最短路径序列。

 

数据抽象

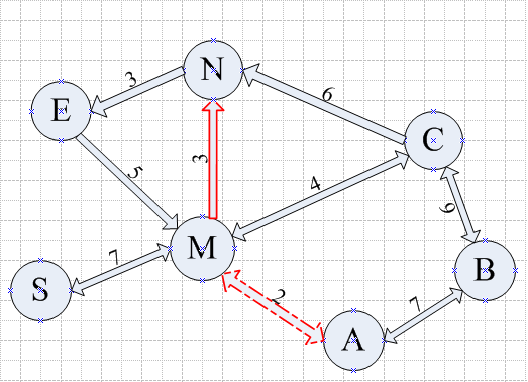
实际的GPS导航路径规划是求点对点之间的一条最优路径，数据中需要包括点与点之间的邻接信息。这种以点的方式存储的数据信息在用Dijkstra算法做路径规划的时候有很大的缺点。实际交通网络包括左右转弯以及U-turn等，以点的方式存储数据对于没有U-turn的网络来说（实际交通网络大多数都有U-turn）是没有问题的，但是对于包含U-turn的交通网络来说就会出现问题。因为Dijkstra算法SettledList集合中的节点是不可以重复访问的，这就导致路径无法返回到之前求出最短路径的节点上去，即无法做U-turn。如下图所示： 

 

 图1：Non U-turn

说明：1.S为起点，E为终点。

            2.双向箭头表示两点间是双向通路。

            3.S无法直接经过M抵达N（实际道路的交通限制，不允许在M处左转）

            4.M和A之间的双向通路在A端可以做U-turn。

对于上图，从S到E的最短路径显然是S->M->A->(U-turn)M->N->E（Cost=7+2+2+3+3=17）. 但是对于这种情况的道路，用点信息数据来表示的话是无法找到这样的一条最短路径的。用Dijkstra算法，当迭代到A点的时候，由于M点已经是一个settled了的点，路径中不会返回至M，而是经过B->C(由C同样不会到达M)->N->E（Cost=7+2+7+6+6+3=31）.这样计算出来的“最短路径”显然是不符合实际的。因此现在的导航路径数据都是采用记录弧段的方式来存储的，我们称之为link,每个link都有一个唯一表示的id，称为linkid。link必须满足以下特征：

            1.非自相交。

            2.与其他link不相交。

如对上面的拓扑结构进行link化，可以得到如下的基于link的道路网络拓扑结构。

 

  图2：Non U-turn（link表示） 

图1和图2的区别主要在：1.图2去除了图1中的顶点。2.图2中的每条弧段都加了一个唯一的linkid标识，括号中的值为该link的weight。对数据link抽象处理以后，整个交通网络就由基于点之间的邻接关系转化为基于link间的邻接关系，此时的数据信息便可以有效解决U-turn的问题了。每条link对应的是实际交通网络中的一条独立的道路，我们可以对link设置一个方向，从起点s到终点e为正方向，从e到s为负方向。显然，其他link L'与该link L的邻接关系只有四种情况：s->s',s->e',e->s',e->e'。用Dijkstra算法迭代的时候需要记录每次访问的邻接关系（四种情况中的一种），从而使算法可以重复访问已经经过的link，这也是可以解决u-turn的关键。如图2所示，原来的从起点S到终点E的路径规划问题已经转化为起始link（id = 100）到终点link（id为106）的路径规划。此时算法是可以找到如下一条路径的(以linkid为路径序列)：100->101->-101->107->106（101->-101是个U-turn）。

 

算法优化

Dijkstra算法的时间复杂度为O(n2)，当处理的数据量大的时候，计算时间会很长。 

可以从以下几个方面进行优化：

1、对OpenedList进行堆优化（二叉堆，二项式堆，或是Fibonacci堆，对最短路径算法来说，Fibonacci堆是比较好的选择，因为相比前两种堆，它的insert操作的时间复杂度为O(1)）。

2、不要将相同的link插入到OpenedList中。

3、如果可以获取每条打开的link的坐标信息，则可以根据这条link到终点link的距离信息来判断是否打开这条link，从而可以一定程度降低算法的搜索空间，这是一个启发因子，指引搜索的趋势往终点方向进行（其实这样做就已经是A*算法了）。