pku acm 1450 解题报告

Gridland
Time Limit:1000MS  Memory Limit:10000K
Total Submit:544 Accepted:360

Description
Background

For years, computer scientists have been trying to find efficient solutions to different computing problems. For some of them efficient algorithms are already available, these are the "easy" problems like sorting, evaluating a polynomial or finding the shortest path in a graph. For the "hard" ones only exponential-time algorithms are known. The traveling-salesman problem belongs to this latter group. Given a set of N towns and roads between these towns, the problem is to compute the shortest path allowing a salesman to visit each of the towns once and only once and return to the starting point.

Problem

The president of Gridland has hired you to design a program that calculates the length of the shortest traveling-salesman tour for the towns in the country. In Gridland, there is one town at each of the points of a rectangular grid. Roads run from every town in the directions North, Northwest, West, Southwest, South, Southeast, East, and Northeast, provided that there is a neighbouring town in that direction. The distance between neighbouring towns in directions North-South or East-West is 1 unit. The length of the roads is measured by the Euclidean distance. For example, Figure 7 shows 2 * 3-Gridland, i.e., a rectangular grid of dimensions 2 by 3. In 2 * 3-Gridland, the shortest tour has length 6.

 

Figure 7: A traveling-salesman tour in 2 ? 3-Gridland.

Input
The first line contains the number of scenarios.

For each scenario, the grid dimensions m and n will be given as two integer numbers in a single line, separated by a single blank, satisfying 1 < m < 50 and 1 < n < 50.

Output
The output for each scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. In the next line, print the length of the shortest traveling-salesman tour rounded to two decimal digits. The output for every scenario ends with a blank line.

Sample Input
2
2 2
2 3

Sample Output

Scenario #1:
4.00

Scenario #2:
6.00

Source
Northwestern Europe 2001

 

 

问题分析方法:

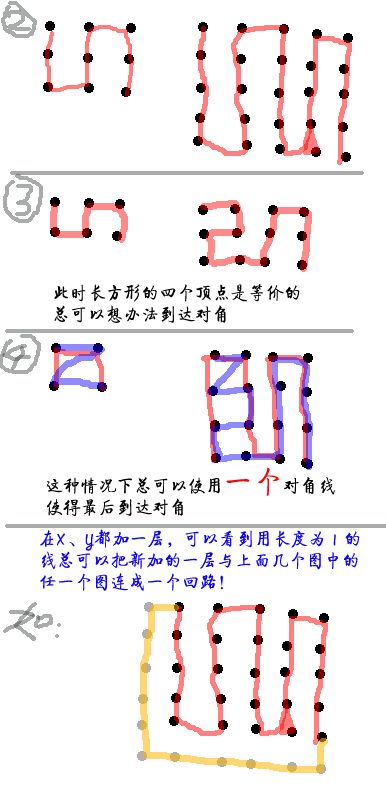
　　用数学归纳法的思想，从少到多的考虑，2*2　2*3　2*4　3*3　3*4　3*5　4*4　4*5　5*5........我们可以发现，一些规律，利用这些规律便可轻易的得出程序！

　　１、过一个结点（城市）有且仅有两条路径（即SALSEMAN走的路）相连。因为每个结点只能走一次，走进结点＋走出结点，只能有一进一走两条路径，应尽量不使用对解线；
　　２、X、 Y（X、Y分别为X、Y轴方向上的结点数）都为奇数时，走蛇型路线（遍历所有结点）只能到对角；
　　３、X、Y为一奇一偶时，走蛇型路线（遍历所有结点）可以走到对角（也可以走到同边最后一个结点）
　　４、X、Y者为偶时，只能走到同边最后一个结点。
　　５、一共有且仅有X*Y条边。每条边同时是一个结点的出边和相邻结点的入边，只要算每个结点匹配一条边就可以了。

 

 

 gcc代码如下：

main() { int total; int m,n; int i; scanf("%d",&total); for(i=1; i <= total ; i++) {  scanf("%d%d",&m,&n);  printf("Scenario #%d:/n",i);  if( (m*n)%2 == 0)   printf("%d.00/n",m*n);  else   printf("%d.41/n",m*n);  printf("/n"); }/*for*/ }