大数乘法--蓝桥杯

欢迎访问我的新博客：http://www.milkcu.com/blog/

原文地址：http://www.milkcu.com/blog/archives/1366855140.html

简述

这是2012年蓝桥杯全国软件大赛预赛（C++本科组）第6题，有图片可知是个简单的大数计算的问题。

推荐链接：《2012蓝桥杯软件大赛预赛题目汇总》

题目描述

    对于32位字长的机器，大约超过20亿，用int类型就无法表示了，我们可以选择int64类型，但无论怎样扩展，固定的整数类型总是有表达的极限！如果对超级大整数进行精确运算呢？一个简单的办法是：仅仅使用现有类型，但是把大整数的运算化解为若干小整数的运算，即所谓：“分块法”。
    如图【1.jpg】表示了分块乘法的原理。可以把大数分成多段（此处为2段）小数，然后用小数的多次运算组合表示一个大数。可以根据int的承载能力规定小块的大小，比如要把int分成2段，则小块可取10000为上限值。注意，小块在进行纵向累加后，需要进行进位校正。

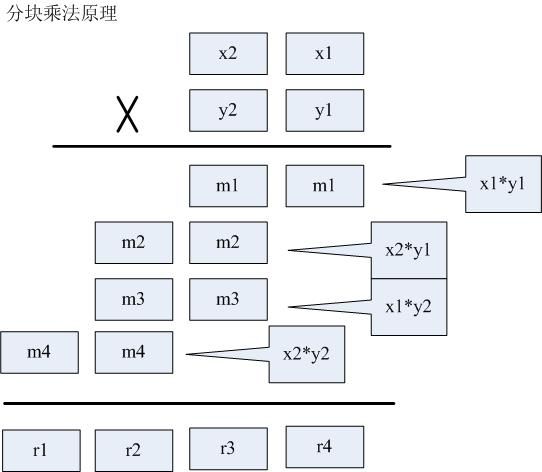
    以下代码示意了分块乘法的原理（乘数、被乘数都分为2段）。

void bigmul(int x, int y, int r[])
{
	int base = 10000;
	int x2 = x / base;
	int x1 = x % base; 
	int y2 = y / base;
	int y1 = y % base; 

	int n1 = x1 * y1; 
	int n2 = x1 * y2;
	int n3 = x2 * y1;
	int n4 = x2 * y2;

	r[3] = n1 % base;
	r[2] = n1 / base + n2 % base + n3 % base;
	r[1] = ____________________________________________; // 填空
	r[0] = n4 / base;
	
	r[1] += _______________________;  // 填空
	r[2] = r[2] % base;
	r[0] += r[1] / base;
	r[1] = r[1] % base;
}


int main(int argc, char* argv[])
{
	int x[] = {0,0,0,0};

	bigmul(87654321, 12345678, x);

	printf("%d%d%d%d\n", x[0],x[1],x[2],x[3]);

	return 0;
}

请分析代码逻辑，并推测划线处的代码。
答案写在 “解答.txt” 文件中
注意：只写划线处应该填的内容，划线前后的内容不要抄写。

分析

这也许是预赛10个题里最简单的一个题，简单的说就是十进制数的进位问题。

源代码

# include <stdio.h>
void bigmul(int x, int y, int r[])
{
	int base = 10000;
	int x2 = x / base;
	int x1 = x % base; 
	int y2 = y / base;
	int y1 = y % base; 

	int n1 = x1 * y1; 
	int n2 = x1 * y2;
	int n3 = x2 * y1;
	int n4 = x2 * y2;

	r[3] = n1 % base;
	r[2] = n1 / base + n2 % base + n3 % base;
	r[1] = n2 / base + n3 / base + n4 % base; // 填空
	r[0] = n4 / base;
	
	r[1] += r[2] / base;  // 填空
	r[2] = r[2] % base;
	r[0] += r[1] / base;
	r[1] = r[1] % base;
}


int main(int argc, char* argv[])
{
	int x[] = {0,0,0,0};

	bigmul(87654321, 12345678, x);

	printf("%d%d%d%d\n", x[0],x[1],x[2],x[3]);

	return 0;
}

最后答案

n2 / base + n3 / base + n4 % base
r[2] / base