轮廓 - 深入分析轮廓
本小节学习轮廓的常用操作,识别和处理,深入理解轮廓的相关算法及原理。
1. 多边形逼近
当需要对图像进行形状分析时,需要使用多边形逼近一个轮廓,使得顶点数目变少,算法原理比较简单,核心就是不断找多边形最远的点加入形成新的多边形,直到最短距离小于指定的精度。OpenCV里面用函数cvApproxPoly()实现。
ApproxPoly
用指定精度逼近多边形曲线
CvSeq* cvApproxPoly( const void* src_seq, int header_size, CvMemStorage* storage,
int method, double parameter, int parameter2=0 );
src_seq
点集数组序列
header_size
逼近曲线的头尺寸
storage
逼近轮廓的容器。如果为 NULL, 则使用输入的序列
method
逼近方法。目前仅支持 CV_POLY_APPROX_DP , 对应 Douglas-Peucker 算法.
parameter
方法相关参数。对 CV_POLY_APPROX_DP 它是指定的逼近精度
parameter2
如果 src_seq 是序列,它表示要么逼近单个序列,要么在 src_seq 的同一个或低级层次上逼近所有序列 (参考 cvFindContours 中对轮廓继承结构的描述). 如果 src_seq 是点集的数组 (CvMat*) , 参数指定曲线是闭合 (parameter2!=0) 还是非闭合 (parameter2=0).
函数 cvApproxPoly 逼近一个或多个曲线,并返回逼近结果。对多个曲线的逼近,生成的树将与输入的具有同样的结构。(1:1 的对应关系).
2. 轮廓的特性概括
轮廓包括一些特性,长度、矩形边界框、面积、圆形和椭圆形边界,轮廓钜等。
3. 轮廓的匹配
实际应用中会有两个轮廓的匹配比较相似度,或者比较一个轮廓和一个抽象模板的的相似度。
简单的方式是比较两个轮廓的轮廓矩。
矩的定义:通过对轮廓上所有点进行积分运算。
计算轮廓矩:cvContoursMoments
归一化的矩(重要):不同大小但是形状相同的物体轮廓应有相同的矩。因此在比对轮廓相似度时通常使用归一化的矩,Hu矩是其中一种较好的方法。但是有一个问题,为什么每个图像要对应7个hu矩呢?
使用Hu矩进行匹配:
double cvMatchShapes( const void* object1, const void* object2, int method, double parameter=0 )
等级匹配:
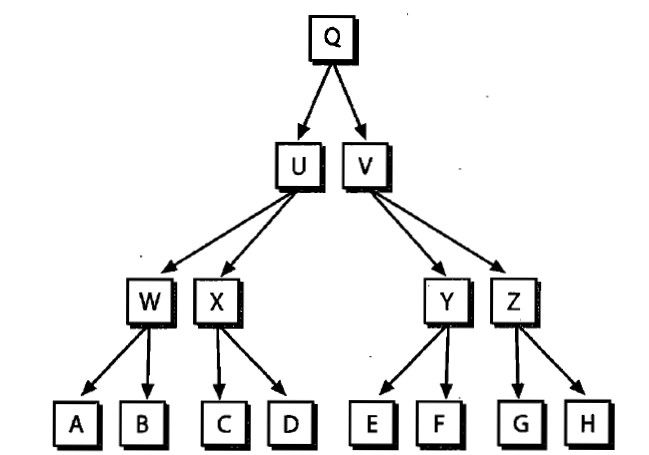
用相似度量度来计算轮廓所有匹配的部分,这就要用到轮廓树,这里的轮廓树不是cvFindContours()函数返回的多个轮廓的继承描述,而是描述一个特定形状(不是多个特定形状)内各部分的等级关系,建立轮廓树的算法很巧妙,要掌握这种思想(见书page285),最后产生的轮廓树是一个二分树。
如图所示的轮廓树,每个节点表示一个三角形,父节点是子节点合并形成的新的三角形:
轮廓的凸包和凸缺陷:
概念很简单,见图就可理解,箭头指的区域就是缺陷,整个手的外部多边形就是凸包。
有三个对应的操作函数:
CvSeq* cvConvexHull2( const CvArr* input, void* hull_storage=NULL,int orientation=CV_CLOCKWISE, int return_points=0 ); //简单计算已知轮廓的凸包
int cvCheckContourConvexity( const CvArr* contour ); //测试轮廓的凸性
CvSeq* cvConvexityDefects( const CvArr* contour, const CvArr* convexhull,CvMemStorage* storage=NULL ); //发现轮廓凸形缺陷
成对几何直方图(PGH):实际上是链码编码直方图(CCH)的一个扩展,CCH是一种直方图,用来统计一个轮廓的Freeman链码编码每一种走法的数字。(Freeman的设计很巧妙,他是对一个多边形的描述,规定8给方向的移动,每个这样的移动有固定的长度和特定的方向,参见page 266)
如图Freeman编码,旋转45度,只需将链码循环平移一个单位即可:
PGH的设计也很好,它规定多边形上的每两个边都有一个夹角、一个最小距离和一个最大距离,并且这些数字被编码到一个二维直方图,无论如何旋转图像,改变图像的大小,直方图都不变,都能得到匹配,即旋转不变性。
如图所示:
转自:http://blog.csdn.net/hitwengqi/article/details/6929523