Data-Intensive Text Processing with MapReduce
同步可能是设计MapReduce算法(一般来说,通常是并行和分布式算法)中最棘手的部分。不同于令人尴尬的并行问题,运行在同一集群不同节点的进程必须及时到达某些节点集合。例如,在节点中分配部分结果到需要的节点上。在一个简单的MapReduce job中,只有一次机会给整个集群同步-----在shuffle(清洗)和sort(排序)阶段中的中间key-value键值对以key分类从mappers复制到reducers的时候。除了上述情况,mappers和reducers独立地运行着,没有任何机制来使他们直接通信。而且,程序员在程序执行时可控制的方面很少,例如:
mapper、reducer运行在那里?(在那个节点)
什么时候mapper、reducer开始或结束?
一个输入键值对由具体那一个mapper处理?
一个中间键值对由具体那一个reducer处理?
然而,有一些技术可以用来控制执行和管理MapReduce中的数据流,总的来说它们是:
1. 构建复杂数据结构作为键和值来存储并和部分结果交互。
2. 在map或reduce任务开始前执行用户自定初始化代码和在map或reduce任务结束前执行用户自定终止代码。
3. 在mappers和reducers传入多样输入或中间值时保持状态。
4. 控制中间值的排序,使reducer会遇到特定的键。
5. 控制键空间的分配,使reducer会遇到特定的键。
要意识到很多算法并不能简单的转换成一个MapReduce的job。它必须经常把复合的算法分解到一个job序列,并需要把一个job中的输出数据变成下一个job的输入数据。很多算法实质上是迭代,它需要重复计算直到达到一些收敛准则-----第五章的图算法和第六章的最大期望值算法就是这种情况。在大多数情况下,收敛的自我检查在MapReduce中不容易实现。普遍的解决方案是用一个外部(非MapReduce)程序作为一个驱动器来协调MapReduce迭代。
这章解释了在Mapduce中怎样用各种技术来控制代码执行和可以用于设计算法的数据流。关注于扩展性---确保算法在应用到不断增长的数据集时没有瓶颈并且高效---确保算法不会因消耗额外的资源由此降低了并行的价值。黄金法则,当然是线性的可伸缩性:算法对于两倍的数据量需要两倍的时间来执行,同理,对于由两倍的节点数执行时间应该减半。
此章组成结构如下:
3.1节介绍了MapReduce中局部聚集的重要概念和一些策略来设计高效的算法来最小化必须通过网络传输的部分结果的数据量。合并器(combiner)的合理使用和(map内合并)in-mapper combining模式也会详细讨论。
3.2节用在大文本集合中建立词语同现矩阵来阐述两个常见的设计模式,我们称为pairs和strips。这两种方法在需要通过大量的观测值跟踪共同事件这类问题很有用。
3.3节展示了同现计数(co-occurrence counts)是怎样用顺序倒转模式转换成相关频率的。Reducer中的计算顺序会被转换为一个排序问题,中间数据被排成序来进行一系列的计算。常常一个reducer需要在单独的元素被加工之前计算一套元素总的统计量。通常,这会被置之不理,但对于“顺序倒转”模式,总数统计应该在单独元素到来之前被计算。这会被认为是违反直觉的:怎样能让我们在单独的元素被加工之前计算一套元素总的统计量?事实的结果是,智能的对特殊的键值对进行排序就能做到。
3.4节提供一个二次排序的常规解决办法,问题的关键是在reduce阶段把键对应的值排序。我们把这种技术称为“键值转换(value-to-key conversion)”。
3.5节涉及到在相关的数据集中执行joins的方法和演示3个不同的方法:reduce端连接, map端连接和基于内存的连接。
3.1局部聚集(local aggregation)
在数据密集的分布式处理环境中,从产生它们的进程到最后消费它们的进程,中间结果的交互是同步中重要的一个方面。在一个集群环境中,除了令人尴尬的并行问题,其它都必须通过网络传输数据。此外,在Hadoop,中间结果是先写到本地磁盘然后再用网络发送出去。因为网络和磁盘因素相对其它因素更加容易成为评价,所以减少中间数据的传输即提高了算法的效率。在MapReduce中,本地中间结果聚集是提高算法效率的一种方法。通过使用combiner(合并器)和通过利用保存不同输入状态的能力,这样做通常能够大体上减少需要从mappers中传输到reducers的键值对数量。
3.1.1 COMBINERS(合并器)和IN-MAPPER COMBINING(MAP内合并)
我们在2.2节中用简单的单词计算例子阐述了本地聚集的各种技术。为了方便,图3.1重现了那个简单的基础算法的伪代码:mapper把每一个term当一条键值对,以term本身作为键,值为1,发送出去;reducers合计部分计数来达到总数。
1: class Mapper
2: method Map(docid a,doc d)
3: for all term t ∈ doc d do
4: Emit(term t, count 1)
1: class Reducer
2: method Reduce(term t; counts [c1, c2, . . .])
3: sum ←0
4: for all count c ∈ counts [c1, c2, . . .] do
5: sum ← sum + c
6: Emit(term t, count sum)
图3.1:MapReduce单词统计算法伪代码(图2.3的再现)
第一个本地聚集的技术是combiner,在2.4节时讨论过。combiner在MapReduce框架中提供一种普通的机制来减少由mappers生成的中间值的数量---我们也可以认为它们是处理mappers输出数据的“迷你reducers”。在这个例子中,合并器统计了每个map任务传来的每个单词个数。这个结果减少了需要通过网络传输的键值对的个数,从集合中所有单词到集合中的部分单词。
1: class Mapper
2: method Map(docid a, doc d)
3: H ←new AssociativeArray
4: for all term t ∈ doc d do
5: H{t} ← H{t} + 1 //Tally counts for entire document
6: for all term t ∈ H do
7: Emit(term t, count H{t})
图3.2:改进型的MapReduce单词统计算法,它使用一个关联数组在每一个文档基础上聚集单词的计数。Reducer和图3.1中的一样。
图3.2展示了改进了的基础算法(mapper被修改,reducer和图3.1的一样)。关联数组(例如java中的map)在mapper中被引进来计算文档中单词的计数:而不是把文档中每个单词的键值对发送出去。考虑到一些词语会经常出现在同一文档中(例如,一篇介绍狗的文章会经常出现“狗”这个单词),这样做可以大量的减少需要发送的键值对的数量,特别是对于长文档来说。
这个基本概念能更进一步,作为图3.3单词统计算法的变种,这个算法的运作严重依赖于2.6节中讲到的hadoop中map和reduce是怎样执行的。回忆,每个map任务都产生一个java mapper对象,它负责处理一堆键值对。在处理键值对之前,mapper的与用户自定代码挂钩的API初始化方法被调用。在这种情况下,我们初始化了一组关联数组来记录单词数。(对每一输入键值对来说)由于它可以在各种Map方法的调用中保持状态,我们可以继续在多个文档间通过关联数组累计部分单词计数,当mapper处理完所有文档后再把键值对发送出去。也就是说,延迟发送中间数据直到运行到伪代码中的close方法。回想起这个API提供一个机会在map方法中所有输入数据中的键值对分配到map任务中执行后执行用户自定代码。
有了这种技术,我们实际上把combiner的功能合并到mapper中。再也不需要运行一个单独的combiner,因为所有本地聚集的情况已经探明。这是一个在MapReduce中比较常见的设计模式,我们称为“in-mapper combining”,以便我们能更方便地在本书中参照这个模式。我们在后面会看到这个模式是怎样应用到不同问题上的。使用这个模式有两个主要好处:
首先,它能够控制本地聚集何时发生和它怎样发生的,相比之下combiner的语义就是在MapReduce的控制下执行。
例如,Hadoop并不保证combiner会用多少次,也就是说它甚至会每次都用。Combiner在执行框架中被作为一个语义维持最优化的提供者,那个会选择使用它,可能会有很多次,或者没有(或者在reduce阶段中)。在某些情况中(虽然不是这个特殊的例子),这种不可预测的情况是无法接受的,所以程序员们经常选择在mappers中执行局部聚集。
其次,使用map内合并(in-mapper combining)通常会比使用combiners更高效。其中一个原因是由于与具体的键值对交互而产生额外的开销。Combiner减少了通过网络传输的中间数据,但实际上没有减少初次发出的键值对数量。图3.2中的算法中,中间键值对仍然在每个文档的基础上生成,只是被combiners减少了些。这个进程涉及不必要的对象的创建和销毁(垃圾处理机制能从容处理),而且还包括对象的序列化与反序列化(当map的输出中间键值对装满内存缓存并需要暂时存放在磁盘时)。相比之下,使用in-mapper combining模式mappers只生成需要通过网络传输给reducer的键值对。
不管怎样也要说说in-mapper combining模式的缺点。首先,它破坏了MapReduce的编程基础,因为状态通过各种输入键值对来保存。最后,它没什么大不了的,因为实事求是地对效率的担忧经常胜过纯理论的,但是实践也是很重要的。通过各种输入实例保存状态意味着算法的行为会依赖于遇到输入键值对时的顺序。这样容易产生潜在的排序依赖错误,它在普通情况下难以调试大的数据集(虽然in-mapper combining的正确性在单词统计的例子上很容易说明)。其次,使用in-mapper combining模式有一个重要的扩展性瓶颈。它严重地依赖于用充足的内存去储存中间结果直到mapper完全处理好输入的所有键值对。在单词统计的例子中,占用内存的多少取决于词典的大少,既然这样那么就有可能mapper会在收集时遇到所有单词。Heap's Law,信息检索中一个熟悉的结果,准确的模拟词典大小的增长对集合大小的影响---稍微出人意料的事实是词典的规模总是在不断扩大。因此,图3.3中的算法将涉及这点,在那些之外的关联数组保持着部分单词计数将不再适用在内存上。
1: class Mapper
2: method Initialize
3: H ← new AssociativeArray
4: method Map(docid a, doc d)
5: for all term t ∈ doc d do
6: H{t} ← H{t} + 1 // Tally counts across documents
7: method Close
8: for all term t ∈ H do
9: Emit(term t, count H{t})
图3.3:演示“in-mapper combining”模式的MapReduce单词统计算法的伪代码,reducer和图3.1一样。
4更多详细资料:注意问题是部分term计数,然而,当集合的大小增加时,其中一个会希望增加输入分割大小值来限制增加的map任务的数量
一个使用in-mapper combining技术时限制内存使用的普遍做法是阻塞键值对和定期清除内存里的数据。这个想法很简单:处理了每N个键值对后就发送这部分结果,而不是所有键值对都处理完后再发送这些中间数据。这可以直接用一个counter变量来跟踪已经处理了的键值对数量。作为一种选择,mapper可以知道自身的内存占用空间和当内存使用不足时清除中间键值对。这两种方法,无论是阻塞值(block size)或内存使用最大值(the memory usage threshold)都要根据经验来用:如果是一个太大的值,mapper会用完内存,但如果值太小,局部聚集的数据又可能丢失。而且,在Hadoop中,物理内存被分配到同一节点的多个同时运行的任务中;这些任务都在竞争着这有限的资源,但因为任务是相互独立的,所以很难有效地去协调使用资源。实际上,受益于不断增加的缓冲值,常常会遇到返回值在执行过程中会逐渐缩小,所以不值得花大力气去寻找设置缓存的最优值(Jeff Dean的个人观点)。
在Mapduce算法中,通过使用局部聚集能增加效率的多少取决于中间值的大小、键值的分布和每个单独任务需要发送键值对的数量。聚集的时机,归根结底是从同一键不同值中得来(不管是否使用combiners或in-mapper combining模式)。在单词统计的例子中,局部聚集之所以高效是因为在一个map任务中很多词语会出现多次。局部聚集也是用来解决减少拖后腿者(看2.3节)即其结果和中间值呈高偏态分布的有效技术。在单词统计的例子中,我们没有过滤频繁出现的词语:因此,没有局部聚集的话,需要计算the个数的reducer相对普通的reducer来说要做很多工作,因此这个reducer就会成为拖后腿者。使用本地聚集(不管使用combiners或in-mapper combining模式),我们大体上减少由频繁出现的词语产生的值,从而缓解减少拖后腿者的问题。
3.1.2 局部聚集算法的正确性
虽然使用combiners可以很好的减少算法的消耗时间,在使用它们时要特别小心。因为在Hadoop中combiner是可选择性的优化手段,算法的正确性并不依赖于combiner的运算能力。在任何MapReduce程序中,reducer的输入键值对类型必须和mapper输出的键值对类型相匹配:这暗示着combiner的输入和输出键值对必须和mapper的输出键值对匹配(像reducer的输入键值对类型那样)。在reduce的计算是交互和协作的例子中,reducer可以作为combiner(像单词统计那个例子)使用(不用修改)。一般来说,combiners和reducers是不可交换的。
想像这样的例子:我们有一个大型数据集,输入键是string类型,输入值是integer类型,我们想计算所有相同键的平均值(rounded to the nearest integer)。现实世界中的例子可能是流行网站的用户操作日志,键代表用户ID,值代表一些用户在网站上的活动,例如在某一会话中停留的时间。这相当于任务会计算基于每一用户的会话平均时间,这将有助于了解用户的特性。图3.4展示了没有用到combiner来完整这个任务的简单算法的伪代码。我们使用一个特别的mapper,它只是把所有的键值对传到reducers(适当地分组和排序)。Reducer记录运行时的最大值和遇到integer的数量。这些信息是用来计算当所有值都处理完后的平均值。平均值最后作为reducer的输出值(输入的string作为键)。
1: class Mapper
2: method Map(string t; integer r)
3: Emit(string t; integer r)
1: class Reducer
2: method Reduce(string t; integers [r1, r2, . . .])
3: sum ← 0
4: cnt ← 0
5: for all integer r ∈ integers [r1, r2, . . .] do
6: sum ← sum + r
7: cnt ← cnt + 1
8: ravg ← sum/cnt
9: Emit(string t, integer ravg)
图 3.4:计算相同key中value的平均值的mapreduce伪代码
这个算法确实可以工作,但是仍然存在像图3.1中的单词统计算法那样的缺点:它需要把所有键值对通过网络从mappers传到reducers,这样非常低效。不像单词统计那例子,在这种情况下reducer不能像combiner那样使用。想象一下如果我们这样做了会发生什么:combiner会计算同一键的任意值的子集,reducer会计算这些结果的平均值。为了更好地说明,我们知道:
Mean(1; 2; 3; 4; 5) != Mean(Mean(1; 2),Mean(3; 4; 5))
一般来说,用一个数据集任意子集的平均值来求平均值和单纯对这个数据集取平均值的结果是不同的。因此这个方法不会得到正确值。
1: class Mapper
2: method Map(string t, integer r)
3: Emit(string t, integer r)
1: class Combiner
2: method Combine(string t, integers [r1, r2, . . .])
3: sum ← 0
4: cnt ← 0
5: for all integer r 2 integers [r1, r2, . . .] do
6: sum ← sum + r
7: cnt ← cnt + 1
8: Emit(string t, pair (sum, cnt)) // 分发总数和计数
1: class Reducer
2: method Reduce(string t, pairs [(s1, c1), (s2, c2) . . .])
3: sum ← 0
4: cnt ← 0
5: for all pair (s, c) ∈ pairs [(s1, c1), (s2, c2) . . .] do
6: sum ← sum + s
7: cnt ← cnt + c
8: ravg ← sum/cnt
9: Emit(string t, integer ravg)
图 3.5:
尝试使用之前提到过的combiner来计算每个key对应value的平均值,combiner中输入和输出键值对类型的不同违背了Mapreduce编程模型的模式。
那么我们怎样合理地利用combiner呢?图3.5做出了一种尝试。Mapper不变,但是我们加入了一个combiner来统计需要计算平均值的数值部分的部分数据。这个combiner会接收每一键值和与之对应的integer值列表,据此计算这些值的总数和遇到integer的数量(即计数)。总数和计数会打包到一个以同一个string作为键的键值对作为combiner的输出发送出去。在reducer中,直到现在,所有我们算法中的键值已经被初始化(变成string,integers)。然而,MapReduce没有禁止使用更复杂的类型,实际上,这代表着一项MapReduce算法设计中的关键技术,我们已经在这章的开头介绍过。我们之后在这本书中还会频繁遇到复杂的键值对问题。
不幸的是,这个算法不能运行。记得combiner必须有着相同的输入输出键值对类型,它必须和mapper的输出类型和reducer的输入类型相匹配。这明显不是这种情况。为了明白在编程模型中为什么必须作出这样的限制,记得combiners只是优化手段,它不会改变算法的正确性。所以让我们移除combiners来看看会发生什么:mapper的输出值类型是integer,所以reducer希望接收一个integer类型的列表来作为值。但reducer实际上是希望传入一个pair类型的列表!算法的正确性可能发生在在mappers输出中运行的combiner上,更确切地说,combiner并不只是运行一次。回忆我们之前讨论过Hadoop并不保证combiners会被调用多少次;可能是零次,一次或多次。这违背了MapReduce的编程模型。
1: class Mapper
2: method Map(string t, integer r)
3: Emit(string t, pair (r, 1))
1: class Combiner
2: method Combine(string t, pairs [(s1, c1), (s2, c2) . . .])
3: sum ← 0
4: cnt ← 0
5: for all pair (s, c) 2 pairs [(s1, c1), (s2, c2) . . .] do
6: sum ← sum + s
7: cnt ← cnt + c
8: Emit(string t, pair (sum, cnt))
1: class Reducer
2: method Reduce(string t, pairs [(s1, c1), (s2, c2) . . .])
3: sum ← 0
4: cnt ← 0
5: for all pair (s, c) 2 pairs [(s1, c1), (s2, c2) . . .] do
6: sum ← sum + s
7: cnt ← cnt + c
8: ravg ← sum/cnt
9: Emit(string t, integer ravg)
图 3.6:计算每个key中value的平均值的mapreduce伪代码。这个代码非常巧妙的使用combiners来实现。
算法的另一个缺点在图3.6中展示,这时候算法是正确的。在mapper,我们发送由整型和1构成的pair值---这相当于一个实例中的部分计数的总和。Combiner分别统计部分总数和部分计数,之后把更新后的总数和计数发送出去。Reducer和combiner类似,唯一不同它是统计最后结果的。实际上,这个算法把一个不能传递的运算(求数字的平均值)转换成能传递的运算(一对数的元素级的总数,在最后有一个额外的分配)。
让我们通过重复之前的实践来证实这个算法的正确性:没有combiners运行时会发生什么?没有combiners的话,mappers会发送pairs(作为值)到reducers。这样的话中间值pairs的数量和输入键值对的数量一样,并且每一个pair值包括一个整型值和1.reducer仍然会达成正确的总数和计数,因此求到的平均值是正确的。现在把combiners加进去:这个算法仍然正确,不管它运行了多长时间,因为combiners只是统计部分总数和计数然后直接传给reducer。值得注意的是虽然combiner的输出键值对类型必须和reducer的输入键值对类型一致,但是reducer可以用不同的数据类型来发送键值对。
1: class Mapper
2: method Initialize
3: S ← new AssociativeArray
4: C ← new AssociativeArray
5: method Map(string t, integer r)
6: S{t} ← S{t} + r
7: C{t} ← C{t} + 1
8: method Close
9: for all term t ∈ S do
10: Emit(term t, pair (S{t},C{t}))
图 3.7:计算关联的value的平均值的伪代码
最后,在图3.7我们展示了一个更加高效的算法来实现in-mapper combining模式。在mapper里面,与键相关的部分总数和计数通过键值对保存在内存上。当所有输入都处理完后才发送中间键值对;与之前例子相同,值是一个由总数和计数组成的对。Reducer和图3.6中的一样。把部分结果统计从combiner移到mapper受到我们在节前讨论过,但在这个例子中,保存中间数据的数据结构在内存的使用上适中,从而使这个变异算法更有吸引力。
3.2 PAIRS(对)和STRIPES(条纹)
在MapReduce程序中同步的一个普遍做法是通过构建复杂的键和值这样一个途径来使数据自然地适应执行框架。我们在之前的章节中涉及到这个技术,即把部分总数和计数“打包”成一个复合值(例如pair),依次从mapper传到combiner再传到reducer。以之前的出版物为基础【54,94】,这节介绍两个常见的设计模式,我们称为pairs(对)和strips(条纹)。
作为一个运行时的例子,我们关注于在大型数据上建立单词同现矩阵,这是语料库语言学和自然语言处理的共同任务。正式来说,语料库中的同现矩阵是一个在语料库中以n个不同单词(即词汇量)为基础的n×n矩阵。一个mij包含单词wi与wj在具体语境(像句子,段落,文档或某些窗口上的m词,m词是应用程序依赖的属性)下共同出现的次数。矩阵的上下三角形是同样的因为同现是一个对称关系,虽然一般来说单词之间的关系不必相对称。例如,一个同现矩阵M,mij是单词i和单词j同现的次数,它通常不能均衡。
这个任务在文本处理和为其它算法提供初始数据时很普遍,例如,逐点信息交互的统计,无人监管的辨别聚集,还有很多,词典语义的大部分工作是基于词语的分布式情景模式,追溯到1950年和1960年的Firth [55] 和 Harris [69]。这个任务也可以应用于信息检索(例如,同义词词典构建和填充),另外一些相关的领域例如文本挖掘。更重要的是这些问题代表着一个从大量观测值中的不相关的joint事件的分布的任务的特殊实例,统计自然语言处理的一个共同任务是MapReduce的解决方案。实际上这里展示的观念在第六章讨论最大期望值算法时也会用到。
除了文本处理,很多应用领域的问题都有相同的特性。例如,大的零售商会分析销售点的交易记录来识别出购买的产品之间的关系(例如,顾客们买这个的话就会想买那个),这有助于库存管理和产品在货架上的摆放位置。同样地,一个智能的分析希望分辨重复的金融交易,它将提供恶意买卖的线索。这节讨论的算法可以解决类似的问题。
很明显,单词同现问题的算法复杂度是O(n2), 其中n是词库大大小,现实中的英语单词全部加起来可能有10万多个,在web规模中甚至达到10亿个。如果把整个单词同现矩阵放到内存中,计算这个矩阵是非常容易的,然而,由于这个矩阵太大以致内存放不下,一种在单机上很慢无经验的实现是把内存保存到磁盘上。虽然压缩计数能够提高单机构建单词同现矩阵的规模,但是它明显存在限制伸缩性的问题。我们会为这个任务提供两个MapReduce算法来使其能适用于大规模的数据集。
1: class Mapper
2: method Map(docid a, doc d)
3: for all term w ∈ doc d do
4: for all term u ∈ Neighbors(w) do
5: Emit(pair (w, u), count 1) //出现一次发送一次计数
1: class Reducer
2: method Reduce(pair p, counts [c1, c2, . . . ])
3: s ← 0
4: for all count c 2 counts [c1, c2, . . . ] do
5: s ← s + c //统计出现的次数
6: Emit(pair p, count s)
图 3.8: 大数据集中计算单词的同现矩阵的伪代码
图3.8展示了我们称之为“pairs”的第一个算法的伪代码。像往常一样,文档的id和相关的内容组成输入的键值对。Mapper处理每一个输入文档和发送同现词对作为键1(即计数)作为值的中间键值对。这由两个嵌套循环来完成:外循环遍历每一个词语(pair中的左元素),内循环遍历第一个词语(pair中的右元素)的所有邻接词。MapReduce执行框架保证同一键的所有值都会在reducer中集合。因此,在这种情况下reducer只是用同一单词同现键值对获得文档中joint事件的绝对数量来进行简单的统计,这些值将作为最终键值对发送出去。每一个键值对相当于单词同现矩阵的一个值。这个算法说明了使用复杂的键来协调分布式计算。
1: class Mapper
2: method Map(docid a, doc d)
3: for all term w ∈ doc d do
4: H ← new AssociativeArray
5: for all term u ∈ Neighbors(w) do
6: H{u} ← H{u} + 1 //统计和w同时出现的单词的计数
7: Emit(Term w, Stripe H)
1: class Reducer
2: method Reduce(term w, stripes [H1,H2,H3, . . . ])
3: Hf ← new AssociativeArray
4: for all stripe H ∈ stripes [H1,H2,H3, . . . ] do
5: Sum(Hf ,H) //按元素进行统计Element-wise sum
6: Emit(term w, stripe Hf )
图 3.9:用stripes的方法来计算单词的同现矩阵, 注:element wise就是按元素进行运算,将两个不同矩阵内部的对应元素相乘
图3.9展示了另一个可选的方法---“stripes”方法。和pairs方法一样,同现词的键值对由两个嵌套循环来生成。然而,和之前方法主要的不同是,同现的信息首先被存放在关联数组H中而不是发送每一个同现词对的中间键值对。Mapper用词语作为key并把对应的关联数组作为value发送出去,每一个关联数组记录着某一个词语的相邻元素(如:它的上下文中出现的词语)的同现次数。MapReduce执行框架会使所有相同key的关联数组到reduce阶段一起处理。Reducer根据相同的key来进行统计运算(element-wise sum),积累的计数相当于同现矩阵中的同一个单元(cell)。最后的关联数组以相同的词作为主键发送出去。相比于pairs方法,stripes方法中每个最终键值对包含同现矩阵中的一行。
很明显,pairs算法相对stripes算法来说要生成很多键值对。Stripes表现得更加紧凑,因为pairs算法中的左元素代表着每一同现词对。Stripes方法则生成更加少而短的中间键,因此,在框架中执行时不需要太多的排序。但是,stripes的值更加复杂,也比pairs算法有着更多的序列化与反序列化操作。
这两种算法都得益于使用combiners,因为它们运行在reducers(额外和元素智能的关联数组的个数)的程序都是可交换和可结合的。然而,stripes方法中的combiners有更多的机会执行局部聚集,因为主要是词库占用空间,关联数组能在mapper多次遇到某个单词时被更新。相比之下,pairs的主要占用空间的是它自己和词典相交的空间,一个mapper观察到多次同一同现对时只能计数只能聚集(它和在stripes中观察一个单词的多次出现不同)。
对这两种算法而言,之前章节提到的in-mapper combining优化方法也可以对它们使用;因为这个修改比较简单我们把它留给读者作为练习。然而,上面提到的警告仍然有:因为缺少中间值的存储空间,pairs方法将有比较少的机会做到部分聚集。缺少空间也限制了in-mapper combining的效率,因为在所有文档都被处理之前mapper就有可能已经用完了内存,这样就必须周期地发送出键值对(更多地限制执行部分聚集的机会)。同样地,对stripes方法来说,它的内存的管理对于简单的单词统计例子来说更加复杂。对于常见的词语,关联数组会变得特别大,需要周期地清除内存中的数据。
考虑到每个算法潜在的伸缩性瓶颈是重要的。Stripes方法假定,在任何时候,每一个关联数组都要足够小来使之适合内存---否则,内存的分页会显著地影响性能。关联数组的大小受限于词典大小,而词典大小和文档的大小无关(回忆之前讨论过的内存不足问题)。因此,当文档的大小增加时,这将成为一个紧迫的问题---可能对于GB级别的数据还没有什么,但可以肯定未来将常见到的TB和PB级别的数据一定会遇到。Pairs方法,在另一方面,没有这种限制,因为它不需要在内存中保存中间数据。
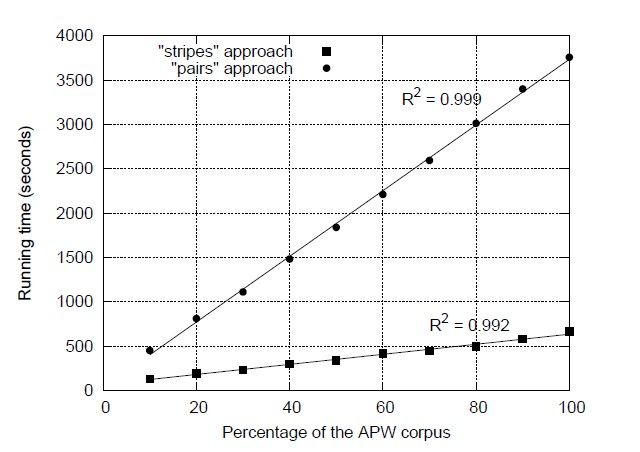
鉴于此讨论,那一个方法更快呢?这里我们引用已发表的结果[94]来回答这个问题。我们在Hadoop中实现了这两个算法,并把它们应用在美联社Worldstream栏目(APW)中总计5.7GB的由2.27百万个文档组成的文档集中。在Hadoop中运行之前,文档集需先做下面处理:把所有XML标记移除,然后是用Lucene搜索引擎提供的基本工具来做分词和去除停止词。了更有效的编码所有分词都被唯一的整数代替为。图3.10对比了pairs和stripes在同一文档集中运行时的不同分数,这个实验是执行在有19个节点的Hadoop集群中,每个节点有一个双核处理器和两个磁盘。
这个结果说明了stripes方法比pairs方法要快很多:处理5.7GB的数据分别用666秒(11分钟)和3758秒(62分钟)。Pairs方法中的mappers生成26亿个总计31.2GB的中间键值对。经过combiners处理后,减少到11亿个键值对,这确定了需要通过网络传输的中间数据的数据量。最后,reducers总共发送1.42亿个最终键值对(同现矩阵中不为零的值的数量)。在另一方法,Pairs方法中的mappers生成6.53亿个总计48.1GB的中间键值对。经过combiners处理后,只剩0.288亿个键值对,最后reducers总共发送169万个最终键值对(同现矩阵中的行数)。像我们期望那样,stripes方法提供更多的机会来让combiners聚集中间结果,因此大大的减少了清洗(shuffle)和排序时的网络传输。图3.1.0也看到了两种算法展现出的高伸缩性---输入数据数量的线性。这由运行时间的线性回归决定,它产生出的R2 值接近1。
图 3.10: 使用不同百分比的APW文集作为实验数据测试pairs和stripes算法计算单词的同现矩阵所使用的时间,这个实验的环境是一个有着19个子节点的Hadoop集群,每个子节点都有两个处理器和两个硬盘。
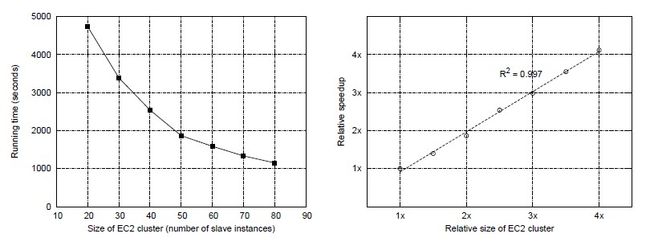
图 3.11:(左边)用不同规模的EC2服务器组成的Hadoop集群来测试stripes算法在APW文集中执行的时间。(右边)根据增加Hadoop集群的规模得到的标度特征(相对的运行速度的提升)。
额外的一系列实验探索了stripes方法另一方面的伸缩性:集群的数量。这个实验可以用亚马逊的EC2服务来做,它允许用户很快地提供聚群来,EC2中的虚拟化计算单元被称为实例,用户根据实例的使用时间来交费。图3.11(左)展示了stripes算法的时间(同一数据集,与之前相同的设置),在不同数量的集群上,从20个节点的“小”实例到80个节点的实例(沿着x坐标)。运行时间由实心方块标示。图3.11(右)重构同样的结果来说明伸缩性。圆圈标出在EC2实验中规模的大小和增速,关于20个节点的集群。这个结果展示了非常理想的线性标度特征(即加倍集群数量使任务时间加快一倍)。这由线性回归中R2值接近1决定的。
从抽象层面看,pairs和stripes算法代表两个计算大量观测值中的重现事件的不同方法。这两个算法抓住了很多算法的特点,包括文本处理,数据挖掘和分析复杂生物资料。由于这个原因,这两种设计模式可以广泛而且频繁地用在不同的程序中。
总的来说,pairs方法分别记录每个同现事件,stripes方法记录所有重现时间关心的调节事件。我们把整个词典拆分成b个部分(即通过哈希查找),wi的同现词会分成b个小的“子stripes”,与10个不同的键分开(wi; 1), (wi; 2) …(wi; b)。这是应对stripes方法中内存限制的合理方法,因为每个子stripes会更小。对b=|V|而言,|V|是词典大小,这与pairs方法是相同的。对b=1而言,这与标准的stripes方法相同。
3.3计算相对频率
让我们在之前讲到的pairs和stripes算法的基础上继续在大型数据集上构建重现矩阵M。回忆在这个大的n×n矩阵中华,当n=|V|(词典大小),元素mij包含单词wi与wj在具体语境下共同出现的次数。无约束的计数的缺点是它没有考虑到实际上有些词会比其它词更加频繁地出现。单词wi可能比wj出现的次数多因为其中一个可能是常用词。一个简单的解决方法是把无约束的计数转变为相对频率,f(wj |wi)。那怎样统计在有wi的上下文中出现的wj频率?可以用下面的公式计算:
f(wj jwi) = N(wi;wj)/ ∑w’ N(wi,w0) (3.1)
在这里,N(.,.)标明一个特殊的同现次对在数据集中被观测到的次数,我们需要统计joint事件(单词的同现),以我们知道的边界(控制变量与其它变量同现的计数的总数)把它分割。
用stripes方法可以直接计算相关频率。在reducer中,和控制变量(在上面的例子中是wi)一起出现的所有词语的个数在关联数组中会用到。因此,能够计算这些数的总值来达到边界(即∑w0 N(wi;w0)),然后用边界值分割所有joint事件来取得所有单词的相关频率。这个实现必须对图3.9的算法做下小修改,并且用来说明把复杂的数据结构用在MapReduce的分布式计算环境中。虽然合适的key和value其中一个就可以使用MapReduce执行框架来把需要计算的数据集中起来。要知道和之前的一样,这个算法也是假设把每一个关联数组存到内存中。
那怎样用pairs方法来计算相对频率呢?在pairs方法中,reducer把接受到的(wi,wj)作为key计数作为value。单单用这个无法计算f(wj |wi)因为我们没有边界值。幸运地,与mapper一样,reducer可以通过多个key来保存状态。在reducer里面,我们可以把和wi同时出现的所有词缓存到内存中,实际上是用stripes方法来建立关联数组。要让它可行,我们还需定义pair的排序顺序来让key先用左边词然后用右边词排序。有个这个排序,我们可以很容易地发现与我们用(wi)做条件的词相关的所有pairs是否都出现。在这个时候我们可以通过保存在内存中的数据来计算相对频率,然后在最终键值对中把结果发送出去。
还需要修改一个地方来使算法工作。我们必须保证左边单词相同的所有pairs都发送到同一reducer中。不幸的是,它不会自动发生:回忆起默认的partitioner是基于中间键的哈希值,以reducers的数量为模。对于一个复杂的键,用来计算哈希值。作为结果,不敢保证,例如,(dog,aardvark)和(dog,zebra)指定到同一reducer。为了产生期待的行为,我们必须定义一个自定partitioner来只关注于左边的单词。就是说,partitioner应该只是基于左边单词的哈希算法来分割。
这个算法可以工作,但它有着和stripes方法一样的缺点:当文档集的数量增长时,词典大小也跟着增加,在某些时候有可能没有足够的内存来存储所有的同现词和我们监控的词的个数。为了计算同现矩阵,使用pairs方法的优点是不会遇到内存瓶颈的问题。有没有一种方法来修改pairs方法使之保留这个优势?
后来人们发现,这样的算法确实是可行的,虽然它需要MapReduce中的一些协调机制。数据到达reducer的顺序是否正确的洞察力。如果有可能以某种方式来使在reducer中计算(或有权使用)边界值在处理joint计数之前,reducer就可以简单的通过边界值拆分joint计数来计算相对频率。“之前”和“之后”的通知可以通过键值对的顺序来捕获,它可以明确地控制在程序员手中。程序员可以定义键的排序顺序来让先要处理的数据在reducer中比后需要处理的数据先处理。然而,我们仍然需要计算边界计数。回忆在基本的pairs算法中,每一个mapper发送一个以同现词对为键的键值对。为了计算相关频率,我们修改了mapper,使它发送出以表单(wi,*)为“特殊”键,值为1的键值对,这代表着单词对对边界值的贡献。通过使用combiners,这些部分边界计数会在发送给reducer之前先做聚集。作为选择,使用in-mapper combining模式可以更加有效地聚集边界计数。
在reducer中,我们必须保证特殊键值对表示部分边界值在普通键值对表示joint次数之前执行。这通过定义keys的排序顺序来完成,然后包含表单(wi; *)的特殊标志的pairs
排在任何其它wi为左单词的键值对的前面。另外,和之前一样,我们必须也定义一个partitioner来观察每一个pair中的左单词。通过恰当的数据排序,reducer能直接计算相对频率。
图3.12是一个真实的例子,它列出了reducer会遇到的键值对列表。首先,reducer面对的是以(dog,*)为特殊键和多个值,每个值都代表从map阶段(在这里假设无论combiners或in-mapper combining,这些值都是代表部分聚集的计数)得到的部分边界贡献的键值对。Reducer累计这些计数来达到极限值∑w’ N(dog,w’)。reducer保存这些值来计算子序列的键。从(dog,*)开始,reducer会遇到一系列代表joint计数的键;第一个的键是(dog, aardvark)。与这个键相关的是在map阶段生成的部分joint计数(在这里是两个不同的值)。统计这些计数可以得出最终joint计数,即dog和aardvark在整个集合中同时出现的次数。在这点上,因为reducer已经知道了极限值,通过简单的计算就可以计算相关频率。所有子joint计数都用相同的方法处理。当reducer遇到下一个特殊的键值对(doge; *)时,reducer重置它的内部状态并开始重新计算下一轮的极限值,因为只有极限值(一个整数)需要存储。不需要缓存单独的同现词的统计数,因此,我们消除了之前算法的伸缩性瓶颈。
Key values
(dog,*) [6327, 8514, . . .] 计算总数: ∑w’ N(dog,w’) = 42908
(dog, aardvark) [2,1] f(aardvark|dog) = 3/42908
(dog, aardwolf) [1] f(aardwolf|dog) = 1/42908
. . .
(dog, zebra) [2,1,1,1] f(zebra|dog) = 5/42908
(doge, *) [682, . . .] 计算总数: ∑w0 N(doge,w’) = 1267
. . .
图 3.12:计算相对频率的pairs算法中发送到reducer的一连串键值对例子。它说明了顺序反转模式
这个设计模式,我们称为“顺序反转”,经常出现并且跨很多领域的应用。之所以会这样命名是因为通过适当的协调,我们可以在处理需要计算的数据之前在reducer中存取计算结果(例如,一个聚集统计)。主要的问题是把计算队列转换为一个排序问题。在多数情况下,特定的算法往往需要固定的数据排序方式:通过控制键的排序和键空间的分配,我们可以把需要在特定环境下计算的数据排序后发送到reducer中。这样做大大减少了reducer需要在内存中保存的部分结果的数量。
总结,运用顺序反转模式来计算相关频率的特殊程序需要以下内容:
1.在mapper中为每一个同现词对发送一个特殊的键值对来捕获它对边界值的贡献值。
2.控制中间键的排序顺序,使特殊键值对表示边界贡献值在任何键值对表示joint单词同现次数之前执行
3.定义一个自定partitioner来保证所有左单词相同的pair都传到同一reducer中。
4.通过reducer中的多个键来保存状态,首先计算基于特殊键值对的边界值然后用边界值来分割joint的计数来得到相关频率。
正如我们将在第四章看到的,这个设计模式也可用于构建反向索引,即通过为链接列表恰当地设置压缩参数。
3.4 二次排序
MapReduce在清洗(shuffle)和排序(sort)阶段用键来为中间键值对排序,如果reducer中的计算依赖于排序顺序的话就非常简单(即之前章节说到的顺序反转模式)。然而,如果除了用键排序之外,我们也需要用值来排序呢?Google的MapReduce实现提供了内置的二次排序的机制,它可以保证值是以排序顺序到达的。Hadoop,不幸的是没有内置这种机制。
(t1,m1, r80521)
(t1,m2, r14209)
(t1,m3, r76042)
…
(t2,m1, r21823)
(t2,m2, r66508)
(t2,m3, r98347)
考虑下一个科学实验的传感器的数据例子:有m个传感器每个都在不间断地读数,m有可能是个很大的数。一个传感器的导出数据是这样的,每一个时间戳后的rx代表着真实的传感器读数(在这次讨论中不重要,但可能是一系列的值,一个或多个复杂的记录,或者甚至是图片文件的字节流)。
假设我们想重新构建各个传感器的活性。MapReduce程序来完成这些,搜集原始数据,以传感器的id作为中间键,
m1 → (t1, r80521)
这样做可以使同一传感器的所有读数一起传到reducer中。然而,因为MapReduce并不保证同一键不同值的排序,传感器读数可能不按照预定的顺序排列。最容易想到的解决方案是在处理这些数据之前先缓存这些读数然后以时间戳来排序。然而,现在需要说的是任何在内存中缓存数据的做法都会带来潜在的伸缩性瓶颈。如果我们需要处理高读数频率的传感器或运行了很长时间的传感器呢?如果传感器的读数本身就是一个大并且复杂的对象呢?这个方法在这个案例中不适用---reducer有可能会因为缓存同一键的所有值而用完内存。
这是一个共同的问题,因为在很多应用程序中,我们希望首先使数据以某种条件(例如,通过传感器的id号)来分组,然后在分组的过程中通过另一种条件(例如,通过时间)排序。幸运的是,有一个普通的解决方案,我们称为“键值转换”(value-to-key conversion)模式。基本思想是把部分值和中间键组成一个混合键,让MapReduce来处理排序。在上面的例子中,我们将发送传感器的id和时间戳作为一个混合键而不是单单用传感器的id作为键:
(m1, t1) → (r80521)
现在传感器读数成为了值。我们必须定义中间键排序顺序来首先使用传感器id(pair的左元素)排序然后用时间戳(pair的右边元素)排序。我们也要实现一个自定的partitioner来让所有同一传感器的对传到同一个reducer中。
经过合适的排序后,键值对会以正确的顺序到达reducer中。
(m1, t1) → [(r80521)]
(m1, t2) → [(r21823)]
(m1, t3) → [(r146925)]
…
然而,现在传感器的读数被拆分到多个键上。Reducer就必须保存之前的状态和跟踪当前传感器的读数在那结束,下一个传感器在那开始。
上面讨论的两个方法(缓存和在内存中排序 vs. “键值转换”模式)的权衡是在那执行排序。一个可以直接在reducer中实现二次排序,这可能运行起来比较快但可能会遇到伸缩性瓶颈的问题10。在键值转换中,排序并不是基于MapReduce框架。要知道这个方法可以任意扩展到三次,四次或跟多的排序。使用这个模式的后果是产生更多的键来让MapReduce框架来排序,不过分布式排序是MapReduce擅长的,但是这种做法违背了Mapreduce编程模型的本质。
3.5相关连接(RELATIONAL JOINS)
Hadoop的一个流行应用领域是数据仓库。在一个企业级的环境中,一个数据仓库作为大量数据的存储地点,存储着从销售交易到商品清单几乎所有的信息。一般来说这些数据都是相关的,但是随着数据的日益增长,数据仓库被用来像存储无结构数据那样存储半结构化的数据(例如,查询日志)。数据仓库组成了提供决策支持的商业智能应用程序的基础。普遍认为知识是通过对历史、现在的数据进行挖掘得到的,预测后的数据能带来市场上的竞争优势。
一般来说,数据仓库已经通过关系数据库实现了,特别是经过优化后的联机分析处理(OLAP)。多维度出现在平行数据库中,但用户们发现他们不能通过一个系统今天要处理的数据来衡量成本效益。并行数据库往往是很贵的---好几万一TB的用户数据。经过这几年的发展,Hadoop作为一个数据仓库被广受欢迎。Hammerbacher[68],讨论过Facebook在Oracle数据库上搭建过商业智能应用,后来放弃了,因为喜欢使用自家开发的基于Hadoop的Hive(现在是个开源项目)。Pig [114]是用Hadoop建立的进行大量数据分析的平台并且可以像处理半结构化数据那样处理结构化数据。它原先是由雅虎开发的,但现在是个开源项目。
如果想在样的环境下用Hadoop建立成功的数据仓库和复杂的分析查询应用程序,查看MapReduce怎样控制相关数据是有意义的。这节主要关注于如何在MapReduce中实现相关连接。我们要在这里强调虽然Hadoop已经被应用于处理相关数据,但Hadoop不是一个数据库。并行数据库和MapReduce在OLAP应用的环境下那个更有优势的争论还在继续。Dewitt和Stonebraker,两个在数据库社区的知名人物,在博客中提出MapReduce是巨大的退步11。作为同事,他们做了一系列论证面向行的并行数据库优于Hadoop的基准测试[120, 144]。然而,看看Dean和Ghemawat的反论[47]和不久前尝试的混合架构[1]。
我们必须停止讨论这件充满活力的事,取代它的是关注于讨论算法。从一个应用程序的观点来看,很有可能一个基于数据仓库的数据分析根本不用写MapReduce程序(实际上,基于Hadoop的Hive和Pig都用一种更高级的语言来处理大规模的数据)。然而,了解构成它的基层算法也是有益的。
这个章节展示三个不同的两个数据集之间的相关连接的策略,一般命名为S和T。让我们假设关系S像下面那样:
(k1, s1,S1)
(k2, s2, S2)
(k3, s3, S3)
…
k是我们希望连接的键,sn是数组的唯一id,在sn后的Sn表示数组中的其它属性(在连接中不重要)。同样,假定关系T像下面那样:
(k1, t1,T1)
(k3, t2,T2)
(k8, t3,T3)
…
k是连接键,tn是数组唯一的id,在tn后的Tn表示元组中的其它属性。
为了使这个任务更加具体,我们举一个现实中可能出现的情况:S代表用户资料的集合,k在这个例子中作为主键(例如,用户的id号)。这个元组可能包含人口统计资料例如年龄、性别、收入等。另一个数据集,T,代表用户网上操作的日志。每一个元组相当于用户在一个页面浏览中的网页URL和包含的额外信息,例如在网页上花的时间,产生的广告收入等。k在这个元组中可以认为是用户浏览不同网页的数据集的外键。连接这两个数据集就可以进行分析,例如,根据用户特性来终止他的网络活动(比如一些恶意攻击)。
3.5.1 REDUCE端连接
第一个相关连接的方法是在reduce里面进行连接。这个想法非常简单:我们遍历两个数据集然后发送连接键作为中间键,元组本身作为值。因为MapReduce保证同一键的所有值都会集中起来,所有元组通过连接键分组---这在我们的连接操作中不是必须的。这个方法在数据库社区中称为并行排序合并连接(parallel sort-merge join),详细说来,还有三种情况需要考虑。
首先是最简单的一对一连接,S中的最多一个元组和T中的一个元组共享同一连接键(但可能有这种情况,即S中没有和T共享一个连接键,或反过来)。在这个例子中,上面所说的算法可以正常工作。Reducer将收到像下面那样的键和值列表:
k23 → [(s64, S64), (t84,T84)]
k37 → [(s68, S68)]
k59 → [(t97,T97), (s81, S81)]
k61 → [(t99,T99)]
…
因为我们把连接键作为中间键发送出去,我们可以把它从值中去除以节省空间12。如果一个键有两个值,则其中一个一定来自S另一个一定来自T。然而,回忆在基本的MapReduce编程模式中,并不能保证值的顺序,所有第一个值可能来自S也可能来自T。我们可以继续连接两个数据集和执行额外的计算(例如,用其它属性过滤,计算总数等)。如果一个键只对应一个值,这意味着没有另外数据集的元组和它有相同的连接键,所以reducer什么都不用做。
12中间数据是否压缩并不是很重要
现在让我们考虑下一对多的连接。假设S中的元组有唯一的连接键(即,k是S中的主键),所以S是“一”T是“多”。上面说到的算法仍然可以工作,但当在reducer中处理每一个键时,我们不知道什么时候会遇到与S的元组相关的值,因为值是任意排序的。最简单的解决方法是在内存中缓存所有值,从S中挑选元组,然后与T中的每一个元组相交来执行连接。然而,我们之前已经多次遇到这种情况,它会带来伸缩性瓶颈,因为我们可能没有足够的内存来存储所有相同连接键的元组。
这个问题需要使用二次排序,解决方案就是我们刚才说到的“键值转换”模式。
在mapper中,我们创建一个包含连接键和元组id(从S或T中获得)的混合键而不是简单的把连接键作为中间键发送出去。还有两个地方需要改变:第一,我们必须定义键的顺序来让它先通过连接键排序再通过S的元组id排序最后用T的元组id排序。第二,我们必须定义partitioner来跟踪连接键,使所有有着相同连接键的混合键传到同一reducer中。
应用了“键值转换”模式后,reducer将得到类似下面那样的键值:
(k82, s105) → [(S105)]
(k82, t98) → [(T98)]
(k82, t101) → [(T101)]
(k82, t137) → [(T137)]
…
因为连接键和元组id都在中间键中,我们可以在值中移除它们来节省空间13。当reducer遇到一个新的连接键时,它能保证关联的值是从S中得到的元组。Reducer可以在内存中保存这个元组然后在下一步(直到遇到一个新的连接key)中和T中的元组交互。因为有mapreduce框架来执行排序,所以就不用再缓存元组(与S中的单个不同)。因此,我们消除了伸缩性瓶颈。最后,让我们考虑多对多的连接情况。假设S是个小数据集,上面的算法依然可以工作。想一下在reducer那里会发生什么。
13再次说明,中间数据是否压缩并不是很重要
(k82, s105) → [(S105)]
(k82, s124) → [(S124)]
…
(k82, t98) → [(T98)]
(k82, t101) → [(T101)]
(k82, t137) → [(T137)]
…
与S的所有元组连接键相同的会先遇到,reducer可以在内存中缓存。Reducer处理T中的每一个元组,并与S中的每一个元组交互。当然,我们假设S中的元组(有共同连接键的)可以放到内存中,这是这个算法的局限(和为什么我们希望控制排序顺序来让小的数据集先传进来)。
在reduce里面连接的基本思想是通过连接键重新分配两个数据集。这个方法并不是特别有效因为它需要在网络中清洗两个数据集。下面来介绍map端连接。
3.5.2 MAP端连接(MAP-SIDE JOIN)
假设我们通过连接键把两个数据集分类。我们可以同步扫描两个数据集来执行连接操作---这在数据库社区被称为合并连接。我们可以通过分割和排序两个数据库来实现平行化。例如,假设S和T都分成10个文件,用连接键以同种方法分割。进一步假设每个文件中的元组通过连接键分类。在这个例子中,我们需要简单的合并连接S的第一个文件和T中的第一个文件,S的第二个文件和T的第二个文件等。在一个MapReduce Job的map阶段中可以通过并行化来完成---这就是map端连接。实际上,我们遍历其中一个数据集(比较大的那个)和在mapper中读取另一个数据集的相关部分来执行合并连接14。这并不需要有reducer参与,除非程序员希望重新分配输出来进行更多的处理。
14这常常预示着这不是一个本地读取
map端的连接远远比reduce端的高效,因为它不需要通过网络来传输数据集。现实中能像期望那样能满足Map端的连接环境?在大多数情况下是这样的。原因是相关连接发生在一个工作流更广的语境中,它可能包含多个步骤。因此,被连接的数据集必须是之前处理的输出(无论是MapReduce jobs还是其它代码)。如果能预先知道工作流程和其相对不变(这都是对于成熟工作流的两个合理的假设),我们可以来让高效的map端连接成为可能(在MapReduce中,通过使用一个自定partitioner和控制键值对的排序顺序)。
对于特别的数据分析,reduce端的连接更加普遍,尽管效率低点,考虑到数据集有多个键,其中一个需要连接---然后无论数据是怎样组成的,map端的连接将需要将数据重新分配。作为选择,使用同一个mapper和reducer重新分配数据集经常是可能发生的。当然,这将导致通过网络传送数据的额外花费。
这是在Hadoop实现的MapReduce中使用map端连接需要记住的最后一个约束。我们假设需要连接的数据集由之前的MapReduce job产生,所以适用于键的约束在reducers的这些jobs中会被发送出去。Hadoop允许reducers发送值与正在处理值的输入键不同的键(即,输入和输出键不需要一样,甚至是不同的类型)15。然而,如果一个reducer的输出键和输入键不同,那么reducer输出的数据集就不需要在特定的partitioner中分割(因为partitioner应用与输入键而不是输出键)。因为map端连接基于对键的不断分割和排序,reducers用来生成参加下一个map端连接的的数据不能发送任何键除了它正在处理的那个。
3.5.3 基于内存的连接(MEMORY-BACKED JOIN)
除了之前提到的两个方法来连接相关数据并平衡MapReduce框架来连接有着同样连接键的元组。还有一个我们称为“基于内存的连接”的基于任意取得探索的同类型方法。最简单的版本是当两个数据集的其中一个在每一个节点中都小于内存时。在这个解决方案中,我们可以把比较小的数据集在每个mapper读取到内存中,基于连接键来获得一个关联数组使减少对元组的任意访问。Mapper的初始化API(看3.11节)可用于这个目的。Mapper然后应用到另一个(大的)数据集,对于每一个输入键值对,mapper检索在内存中的数据集看看是否有一个元组的连接键和它匹配。如果匹配的话就执行连接。这在数据库社区被认为是一个简单的哈希连接[51]。
如果内存放不下其中任意一个数据集呢?最简单的办法是把它分成更小的数据集,即把S分成n个部分,即S = S1 ∪ S2 ∪ .. . ∪Sn。我们可以通过定义n的大小来使每一个部分刚好是内存的大小,然后运行n个基于内存的连接。这样的话,当然,需要流动到另一数据集n次。
15作为对比,2.2节中讲到了Google的实现方法,reducer的输出键必须和它的输入键类型一致。
还有一个替代方案来让基于内存的连接适用与所有数据集都大于内存的情况。一个分布式的键值存储器可以通过多台机器在内存中保存一个数据集,然后去映射其它的数据集。Mapper然后并行地查询这个分布式键值存储器,如果连接键匹配则执行连接16。开源的缓存系统memcached适用于这种情况,因此我们把这种方法称为memcached连接。更多有关这个方法的信息参考技术报告[95]。
这章提供一个设计MapReduce算法的指导。特别地,对于常见问题我们展示了很多设计模式来解决。总的来说,它们是:
“In-mapper combining”(map内合并),combiner函数被移到了mapper里面,mapper通过多个输入记录聚集部分结果,然后只有在局部聚集达到一定量后再发送中间键值对,而不是发送每一个输入键值对的中间输出。
相关的模式“pairs”和“stripes”是通过大量的观测值来跟踪joint事件。在pairs方法中,我们单独地跟踪每一个joint事件,但是在stripes方法中,我们跟踪与相同事件同时发生的所有事件。虽然stripes方法显然更加高效,但是它需要有足够的内存来放下所有的事件,这可能导致伸缩性瓶颈。
“Order inversion”(顺序反转),它的主要思想是把计算的先后顺序转化为一个排序问题。通过仔细的编排,我们在它遇到这个计算中需要的这些数据之前发送这些数据的计算结果(例如,一个聚集统计)给reducer处理。
“Value-to-key conversion”(键值转换),它提供了一个伸缩性解决方案来进行二次排序。通过把部分值移动到键中,我们可以使用MapReduce自身的方法来排序。
最后,在MapReduce编程模型中控制同步归结为能否有效的使用下面的技术:
1.构造复杂的键和值来让需要计算的数据集合起来。这可用于上面所说的所有设计模式。
16为了达到高效的访问分布式键值存储,它常常需要在同步请求()或依赖同步请求之前进行批量查询。
2.在mapper或reducer中执行自定的初始化和终止代码。例如,in-mapper combining模式依赖于在map任务的终止代码中发送中间键值对。
3.在mapper和reducer中通过多重输入保存状态。这可用于in-mapper combining,顺序倒转和键值转换。
4.控制中间键的顺序。这可用于顺序倒转和键值转换。
5.控制中间键空间的分配。这用于顺序倒转和键值转换。
这总结了我们对MapReduce算法设计的概述。现在必须清楚地知道虽然编程模型强制我们根据严格定义的组件来表示算法,但仍然有很多工具来使之适用于这些算法。在下面的一些章节中,我们会关注与特殊的MaoReduce算法:第四章的反向索引,第五章的图处理和第六章的计算期望最大值。