【二分图匹配】【NOI2009】变换序列
【问题描述】
对于N个整数0,1, ……,N-1，一个变换序列T可以将i变成Ti，其中
且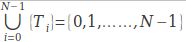
。
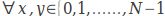，定义x和y之间的距离
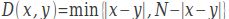。给定每个i和Ti之间的距离D(i,Ti)，你需要求出一个满足要求的变换序列T。如果有多个满足条件的序列，输出其中字典序最小的一个。
说明：对于两个变换序列S和T，如果存在p<N，满足对于i=0,1,……p-1，Si=Ti且Sp<Tp，我们称S比T字典序小。
【输入文件】
输入文件transform.in的第一行包含一个整数N，表示序列的长度。接下来的一行包含N个整数Di，其中Di表示i和Ti之间的距离。
【输出文件】
输出文件为transform.out。
如果至少存在一个满足要求的变换序列T，则输出文件中包含一行N个整数，表示你计算得到的字典序最小的T；否则输出”No Answer”（不含引号）。注意：输出文件中相邻两个数之间用一个空格分开，行末不包含多余空格。
【输入样例】
5
11 2 2 1
【输出样例】
12 4 0 3
【数据规模和约定】
20%的数据中N≤50；
60%的数据中N≤500；
100%的数据中N≤10000。
解法1：
可以非常巧妙地运用二分图逆序匹配，即从最后一个点逆着匹配到第一个点，其中枚举的时候保证从小到大，那么这样匹配出来一定是字典序最小的匹配。
Accode：
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <cstring>
#include <string>
const int maxN = 20010;
struct Edge
{
int v; Edge *next; Edge() {}
Edge(int v, Edge *next): v(v), next(next) {}
} *edge[maxN]; bool marked[maxN];
int Link[maxN], d[maxN], sta[maxN], top, n;
bool Find(int u)
{
for (Edge *p = edge[u]; p; p = p -> next)
if (!marked[p -> v])
{
marked[sta[top++] = p -> v] = 1;
if (Link[p -> v] == -1 || Find(Link[p -> v]))
{Link[p -> v] = u, Link[u] = p -> v; return 1;}
}
return 0;
}
int main()
{
freopen("transform.in", "r", stdin);
freopen("transform.out", "w", stdout);
scanf("%d", &n);
for (int i = 0; i < n; ++i)
{
scanf("%d", d + i); d[i] %= n;
if (d[i] > n >> 1) d[i] = n - d[i];
if (!d[i]) edge[i] = new Edge(i + n, edge[i]);
else if (i + d[i] == i - d[i] + n)
edge[i] = new Edge((i + d[i]) % n + n, edge[i]);
else
{
if (i - d[i] < 0)
edge[i] = new Edge(i - d[i] + (n << 1), edge[i]);
if (i + d[i] < n)
edge[i] = new Edge(i + d[i] + n, edge[i]);
if (i - d[i] > -1)
edge[i] = new Edge(i - d[i] + n, edge[i]);
if (i + d[i] >= n)
edge[i] = new Edge(i + d[i], edge[i]);
}
}
//建图时先建较大边，再建较小边（链表插入过后会反过来）。
memset(Link, 0xff, sizeof Link);
for (int i = n - 1; i > -1; --i)
{
top = 0;
if (!Find(i)) {printf("No Answer\n"); return 0;}
for (int i = 0; i < top; ++i) marked[sta[i]] = 0;
}
for (int i = 0; i < n; ++i) printf("%d ", Link[i] - n);
return 0;
}
解法2：先找出一个可行的匹配，再将其修正为字典序最小的匹配。
若从小到大修正，则在修正的时候加一个限制，即不能修改之前匹配过的点。
Accode：
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <cstring>
#include <string>
const int maxN = 20010;
struct Edge
{
int v; Edge *next; Edge() {}
Edge(int v, Edge *next): v(v), next(next) {}
} *edge[maxN]; bool marked[maxN];
int Link[maxN], d[maxN], sta[maxN], Lim = -1, top, n;
bool Find(int u)
{
if (u <= Lim) return 0;
for (Edge *p = edge[u]; p; p = p -> next)
if (!marked[p -> v])
{
marked[sta[top++] = p -> v] = 1;
if (Link[p -> v] == -1 || Find(Link[p -> v]))
{Link[p -> v] = u, Link[u] = p -> v; return 1;}
}
return 0;
}
int main()
{
freopen("transform.in", "r", stdin);
freopen("transform.out", "w", stdout);
scanf("%d", &n);
for (int i = 0; i < n; ++i)
{
scanf("%d", d + i); d[i] %= n;
if (d[i] > n >> 1) d[i] = n - d[i];
if (!d[i]) edge[i] = new Edge(i + n, edge[i]);
else if (i + d[i] == i - d[i] + n)
edge[i] = new Edge((i + d[i]) % n + n, edge[i]);
else
{
if (i - d[i] < 0)
edge[i] = new Edge(i - d[i] + (n << 1), edge[i]);
if (i + d[i] < n)
edge[i] = new Edge(i + d[i] + n, edge[i]);
if (i - d[i] > -1)
edge[i] = new Edge(i - d[i] + n, edge[i]);
if (i + d[i] >= n)
edge[i] = new Edge(i + d[i], edge[i]);
}
}
memset(Link, 0xff, sizeof Link);
for (int i = 0; i < n; ++i)
{
top = 0;
if (!Find(i)) {printf("No Answer\n"); return 0;}
for (int i = 0; i < top; ++i) marked[sta[i]] = 0;
}
for (int i = 0; i < n; ++i) if (Link[i] - edge[i] -> v)
//若当前匹配i的并不是较小的边，则尝试修正。
{
top = 0; Lim = i; int tmp = Link[edge[i] -> v];
Link[i] = edge[i] -> v; Link[edge[i] -> v] = i;
Link[edge[i] -> next -> v] = Link[tmp] = -1;
if (!Find(tmp))
{
Link[i] = edge[i] -> next -> v;
Link[edge[i] -> next -> v] = i;
Link[edge[i] -> v] = tmp;
Link[tmp] = edge[i] -> v;
} //修正不成功则还原。
for (int i = 0; i < top; ++i) marked[sta[i]] = 0;
}
for (int i = 0; i < n; ++i) printf("%d ", Link[i] - n);
return 0;
}