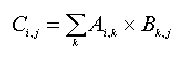[动态规划]UVA348 - Optimal Array Multiplication Sequence

Optimal Array Multiplication Sequence

Given two arrays A and B, we can determine the array C = A B using the standard definition of matrix multiplication:

The number of columns in the A array must be the same as the number of rows in the B array. Notationally, let's say that rows(A) andcolumns(A) are the number of rows and columns, respectively, in the A array. The number of individual multiplications required to compute the entire C array (which will have the same number of rows as A and the same number of columns as B) is then rows(A)columns(B) columns(A). For example, if A is a  array, and B is a  array, it will take  , or 3000 multiplications to compute the C array.

To perform multiplication of more than two arrays we have a choice of how to proceed. For example, if X, Y, and Z are arrays, then to compute X Y Z we could either compute (X Y) Z or X (Y Z). Suppose X is a  array, Y is a  array, and Z is a array. Let's look at the number of multiplications required to compute the product using the two different sequences:

(X Y) Z

•  multiplications to determine the product (X Y), a  array.
• Then  multiplications to determine the final result.
• Total multiplications: 4500.

X (Y Z)

•  multiplications to determine the product (Y Z), a  array.
• Then  multiplications to determine the final result.
• Total multiplications: 8750.

Clearly we'll be able to compute (X Y) Z using fewer individual multiplications.

Given the size of each array in a sequence of arrays to be multiplied, you are to determine an optimal computational sequence. Optimality, for this problem, is relative to the number of individual multiplications required.

Input

For each array in the multiple sequences of arrays to be multiplied you will be given only the dimensions of the array. Each sequence will consist of an integer N which indicates the number of arrays to be multiplied, and then N pairs of integers, each pair giving the number of rows and columns in an array; the order in which the dimensions are given is the same as the order in which the arrays are to be multiplied. A value of zero for N indicates the end of the input. N will be no larger than 10.

Output

Assume the arrays are named  . Your output for each input case is to be a line containing a parenthesized expression clearly indicating the order in which the arrays are to be multiplied. Prefix the output for each case with the case number (they are sequentially numbered, starting with 1). Your output should strongly resemble that shown in the samples shown below. If, by chance, there are multiple correct sequences, any of these will be accepted as a valid answer.

Sample Input

3
1 5
5 20
20 1
3
5 10
10 20
20 35
6
30 35
35 15
15 5
5 10
10 20
20 25
0

Sample Output

Case 1: (A1 x (A2 x A3))
Case 2: ((A1 x A2) x A3)
Case 3: ((A1 x (A2 x A3)) x ((A4 x A5) x A6))

题意：

给你2个矩阵A、B，我们使用标准的矩阵相乘定义C=AB如下：

A阵列中栏（column）的数目一定要等于B阵列中列（row）的数目才可以做此2阵列的相乘。若我们以rows(A)，columns(A)分别代表A阵列中列及栏的数目，要计算C阵列共需要的乘法的数目为：rows(A)*columns(B)*columns(A)。例如：A阵列是一个10x20的矩阵，B阵列是个20x15的矩阵，那么要算出C阵列需要做10*15*20，也就是3000次乘法。

要计算超过2个以上的矩阵相乘就得决定要用怎样的顺序来做。例如：X、Y、Z都是矩阵，要计算XYZ的话可以有2种选择：(XY)Z 或者X(YZ)。假设X是5x10的阵列，Y是10x20的阵列，Z是20x35的阵列，那个不同的运算顺序所需的乘法数会有不同：

(XY)Z

• 5*20*10 = 1000次乘法完成(XY)，并得到一5x20的阵列。
• 5*35*20 = 3500次乘法得到最后的结果。
• 总共需要的乘法的次数：1000+3500=4500。

X(YZ)

• 10*35*20 = 7000次乘法完成(YZ)，并得到一10x35的阵列。
• 5*35*10 = 1750次乘法得到最后的结果。
• 总共需要的乘法的次数：7000+1750=8750。

很明显的，我们可以知道计算(XY)Z会使用较少次的乘法。

这个问题是：给你一些矩阵，你要写一个程式来决定该如何相乘的顺序，使得用到乘法的次数会最少。

思路：最优矩阵链乘问题，典型的动态规划题目。

#include<iostream>
#include<cstring>

using namespace std;

const int maxn=100000000;

class Node
{
public:
    int x,y;
}node[15];

int num;
int dp[15][15],s[15][15];

void printpath(int i,int j)
    {
        if(i==j) cout<<"A"<<i+1;
        else
            {
                cout<<"(";
                printpath(i, s[i][j]);
                cout<<" x ";
                printpath(s[i][j]+1, j);
                cout<<")";
            }
    }

int main()
    {
        int pos=0;
        while(cin>>num&&num)
            {
                for(int i=0;i<num;i++)
                    cin>>node[i].x>>node[i].y;
                memset(dp,0,sizeof(dp));
                memset(s,0,sizeof(s));
                int cost;
                for(int l=1;l<num;l++)
                    {
                        for(int i=0;i<num-l;i++)
                            {
                                int j=l+i;
                                dp[i][j]=maxn;
                                for(int k=i;k<j;k++)
                                    {
                                        cost=dp[i][k]+dp[k+1][j]+node[i].x*node[k].y*node[j].y;
                                        if(cost<dp[i][j])
                                            {
                                                dp[i][j]=cost;
                                                s[i][j]=k;
                                            }
                                    }
                            }
                    }
                cout<<"Case "<<++pos<<": ";
                printpath(0, num-1);
                cout<<endl;
                //cout<<dp[0][num-1]<<endl;
            }
        return 0;
    }