IT求职整理Ⅲ---常见排序算法小结

基础理解：

维基百科排序算法：http://zh.wikipedia.org/wiki/%E6%8E%92%E5%BA%8F#.E7.A9.A9.E5.AE.9A.E7.9A.84

强烈推荐：常见排序算法小结http://blog.csdn.net/whuslei/article/details/6442755?reload

 

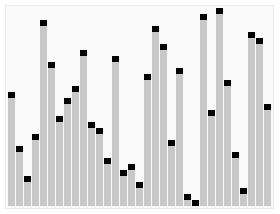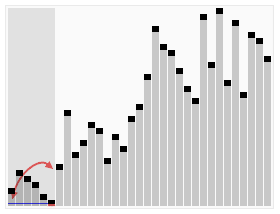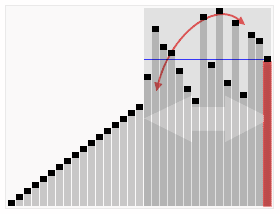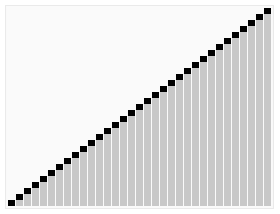
图形化加深理解：

可视化的排序过程：http://coolshell.cn/articles/3933.html

一个排序算法比较的网站：http://www.sorting-algorithms.com/

• 冒泡排序（直接交换排序）（稳定）

算法的步骤如下：

1比较相邻的元素。如果第一个比第二个大，就交换他们两个。

2对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。

3针对所有的元素重复以上的步骤，除了最后一个。

4持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

 

#include<stdio.h>

#defineLENGTH 8//升序排序
voidmain() {
    int i, j, tmp, number[LENGTH] = {95, 45,15, 78, 84, 51, 24, 12};
 //与上面三个伪码不同，从后往前排

    for (i = 0; i < LENGTH; i++) {
        for (j = LENGTH - 1; j > i; j--) {
            if (number[j] < number[j-1]) {
                tmp = number[j-1];
                number[j-1] =  number[j];
                number[j] = tmp;
            }
        }
    }
 
    for (i = 0; i < LENGTH; i++) {
        printf("%d ", number[i]);
    }
    printf("\n");
}

使用标志的冒泡排序

#include<iostream>
usingnamespace std;
voidbubble_sort(int d[], int size)
{
//#假定两两交换发生在数组最后的两个位置#%
         int exchange = size - 1;
while(exchange)
         {//#记录下发生数据交换的位置#%
                   int bound = exchange;
                   exchange= 0; //#假定本趟比较没有数据交换#%
                   for(int i = 0; i < bound;i++)
                   {        if (d[i] > d[i + 1])
                            {        int  t = d[i];
                                     d[i] = d[i+ 1];
                                     d[i + 1] =t;
 
                                    exchange= i;
                            }
                   }
         }
}
intmain (int argc, char * const argv[])
{
         int a[] = {3, 5, 3, 6, 4, 7, 5, 7, 4};
         bubble_sort(a, sizeof(a) / sizeof(*a));
         for(int i = 0; i < sizeof(a) /sizeof(*a); i++)
                   cout << a[i] << '';
         cout << endl;
 
    return 0;
}
 

• 直接插入排序（稳定）：

一般来说，插入排序都采用in-place在数组上实现。具体算法描述如下：

1从第一个元素开始，该元素可以认为已经被排序

2取出下一个元素，在已经排序的元素序列中从后向前扫描

3如果（从后往前已排序）该元素大于新元素，将该元素往前移到下一位置
4重复步骤3，直到找到已排序的元素小于或者等于新元素的位置

5将新元素插入到该位置后

6重复步骤2~5

void insertSort(intarray[],int n) //对R[0...n-1]按递增有序进行直接插入排序
{        int temp,j;
         for(int i=1;i<n;i++)
         {        temp=array[i];
                   j=i-1;//在有序子区间array[0...i-1]中从右往左查找R[i]的插入位置
                   while(j>=0 &&array[j]>temp)
                   {
                            array[j+1]=array[j];//将关键字大于R[i]的记录依次后移，否则跳出
                            j--;
                   }
                   array[j+1]=temp; //在j+1处插入R[i]
         }
}

• 直接选择排序（不稳定）

它的工作原理如下。首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。具体做法是：选择最小的元素与未排序部分的首部交换，使得序列的前面为有序。 

void SelectSort(int array[], int n)
{      int min,temp,i,j;
         for(i=0;i<n-1;i++)//R[0…N-2]共N-1个已排序元素
         {
                   min=i;
                   for(j=i+1;j<n;j++)//在[i..N-1]找出未排序中最小的序号
                            {
                                     if(array[j]<array[min])
                                     min=j;//记录最小关键字所在位置
                            }
                   if(min!=i)//
                   {        temp=array[i];
                            array[i]=array[min];//交换
                            array[min]=temp;
                   }
         }
};

• 快速排序(升级版交换排序)（不稳定）

快速排序使用分治法（Divide andconquer）策略来把一个串行（list）分为两个子串行（sub-lists）。

步骤为：

1.从数列中挑出一个元素，称为"基准"（pivot），

2.重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。

3.递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

  

//方法一
#include<iostream>
  usingnamespace std;
  voidQuickSort(int array[], int low,int high)
  {   int i=low,j=high,temp;
       if(low<high)
       {
                temp=array[low];
                while(i!=j)
                {        while(j>i&& array[j]>temp) j--;
                         if(i<j){array[i]=array[j];i++;}
 
                         while(i<j &&array[i]<temp) i++;
                         if(i<j){array[j]=array[i];j--;}
                }
                array[i]=temp;
                QuickSort(array, low,i-1);
                QuickSort(array, i+1,high);
       }
  }
  int main (intargc, char * const argv[])
  {
       int a[] = {31, 54, 23, 67, 14, 87, 45, 37,4};
       QuickSort(a,0, 8);
       for(int i = 0; i < 9; i++)
                cout << a[i] << ' ';
       cout << endl;
   
      return 0;
  }

方法二
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#define RANDOM(i) (rand()%i)
#define N         15
 
//划分函数
int partion(int a[],int p,int r){
         int x =0;
         int j;
         int i;
         inttemp;
         i = p-1;
         x =a[r];
         for ( j= p; j <=r-1; j++)
         {
                   if(a[j] <=  x)
                   {
                            i++;
                            temp= a[i];
                            a[i]= a[j];
                            a[j]= temp;
 
                   }
         }
         temp =a[i+1];
         a[i+1] =a[r];
         a[r] =temp;
         returni+1;
}
 
void quik_sort(int a[], int p,int r){
         int q;
         if (p< r)
         {
                   q=partion(a,p,r);
                   quik_sort(a,p,q-1);
                   quik_sort(a,q+1,r);
         }
        
}
 
void main(){
 
         intrand_no = 0;
         int i =0;
         inta[N];                              //n表示数组长度
         //srand((int)time(0));               //设置随机数种子
         printf("==============================排序前=========================================");
         printf("\n");
         for(rand_no= 0;rand_no < N;rand_no++)
         {
 
                   a[rand_no]=RANDOM(100);
                   printf("%5d",a[rand_no]);
                  
         }
         printf("\n");
         printf("==============================排序后=========================================\n");
         quik_sort(a,0,N-1);
         for (intj = 0; j < N; j++)
         {
                   printf("%5d",a[j]);
         }
         printf("\n");   
 
 
}
 

希尔排序（升级版插入排序）（不稳定）

思想：希尔排序也是一种插入排序方法,实际上是一种分组插入方法。先取定一个小于n的整数d1作为第一个增量,把表的全部记录分成d1个组,所有距离为d1的倍数的记录放在同一个组中,在各组内进行直接插入排序；然后,取第二个增量d2(＜d1),重复上述的分组和排序,直至所取的增量dt=1(dt<dt-1<…<d2<d1),即所有记录放在同一组中进行直接插入排序为止。