图解数据结构（8）——二叉堆

转载自http://www.cppblog.com/guogangj/archive/2009/10/29/99729.html

首先说说数据结构概念——堆（Heap），其实也没什么大不了，简单地说就是一种有序队列而已，普通的队列是先入先出，而二叉堆是：最小先出。

这不是很简单么？如果这个队列是用数组实现的话那用打擂台的方式从头到尾找一遍，把最小的拿出来不就行了？行啊，可是出队的操作是很频繁的，而每次都得打一遍擂台，那就低效了，打擂台的时间复杂度为Ο(n)，那如何不用从头到尾fetch一遍就出队呢？二叉堆能比较好地解决这个问题，不过之前先介绍一些概念。

完全树（Complete Tree）：从下图中看出，在第n层深度被填满之前，不会开始填第n+1层深度，还有一定是从左往右填满。

再来一棵完全三叉树：

这样有什么好处呢？好处就是能方便地把指针省略掉，用一个简单的数组来表示一棵树，如图：

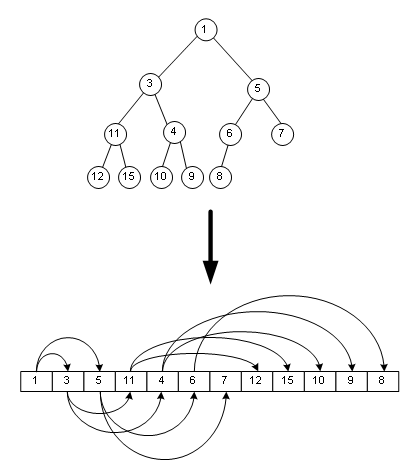
那么下面介绍二叉堆：二叉堆是一种完全二叉树，其任意子树的左右节点（如果有的话）的键值一定比根节点大，上图其实就是一个二叉堆。

你一定发觉了，最小的一个元素就是数组第一个元素，那么二叉堆这种有序队列如何入队呢？看图：

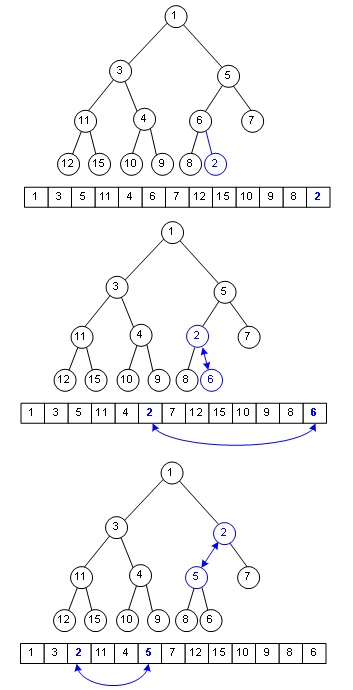
假设要在这个二叉堆里入队一个单元，键值为2，那只需在数组末尾加入这个元素，然后尽可能把这个元素往上挪，直到挪不动，经过了这种复杂度为Ο(logn)的操作，二叉堆还是二叉堆。

那如何出队呢？也不难，看图：

出队一定是出数组的第一个元素，这么来第一个元素以前的位置就成了空位，我们需要把这个空位挪至叶子节点，然后把数组最后一个元素插入这个空位，把这个“空位”尽量往上挪。这种操作的复杂度也是Ο(logn)，比Ο(n)强多了吧？

常用堆的几个功能(一下都是以小顶堆为例(即结点的值都比左右孩子的小))

1)维护堆,向下更新

void min_heapify(int i)    //以i为根,向下更新,使得数组成为小顶堆 
{
	int l = i << 1;          //左孩子位子
	int r = l + 1;           //右孩子位子
	int min = i;
	if(l <= length && heap[l] < heap[min])   //比较大小
	{
		min = l;
	}
	if(r <= length && heap[r] < heap[min])
	{
		min = r;
	}
	if(i != min)       //如果最小的值不是i节点,就交换
	{
		int tmp = heap[i];
		heap[i] = heap[min];
		heap[min] = tmp;
		min_heapify(min);     //继续往下更新
	}
}

2)维护堆，向上更新

void sinkup(int i)    //以i为根,向上更新,使得数组成为小顶堆 
{
	int parent = i >> 1;    //找父节点
	if(heap[parent] > heap[i])    //交换
	{
		int tmp = heap[i];
		heap[i] = heap[parent];
		heap[parent] = tmp;
		if(parent > 1)
			sinkup(parent);//继续向上更新
	}
}

3) 建堆

void min_build()   //建堆 
{
	for(int i = length / 2;i >= 1;i--)    //length为数组长度   
	{
		min_heapify(i);          //从length / 2开始向上更新,不信绘图看看
	}
}

4) 取最小值,即队头元素a[1]

int popheap()
{   
	int min ;
	min=heap[1];       //取队头元素
	heap[1] = heap[length];     //把尾元素放到头
	length--;          
	min_heapify(1);        //向下更新,维护堆
	return min;
}

5)进堆

void pushheap(int x)
{
	length++;        
       	heap[length] = x; // 插到数组最后一个 
      	sinkup(length);     //向上更新,维护堆
}