杭电1023——Train Problem II
Train Problem II
Problem Description
As we all know the Train Problem I, the boss of the Ignatius Train Station want to know if all the trains come in strict-increasing order, how many orders that all the trains can get out of the railway.
Input
The input contains several test cases. Each test cases consists of a number N(1<=N<=100). The input is terminated by the end of file.
Output
For each test case, you should output how many ways that all the trains can get out of the railway.
Sample Input
1 2 3 10
Sample Output
1 2 5 16796HintThe result will be very large, so you may not process it by 32-bit integers.
不得不说,这是一道特别好的题目!我从一开始的找不到思绪,再到了解卡特兰数,了解到大数的乘除法,每一步都收获良多!
先理清一下学到的知识点吧!
1.卡特兰数!又称
卡塔兰数
卡塔兰数是组合数学中一个常在各种计数问题中出现的数列。以比利时的数学家欧仁·查理·卡塔兰
(1814–1894)命名。
卡塔兰数的一般项公式为
前几项为 (OEIS中的数列A000108): 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796,
58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190,
6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ...
性质
Cn的另一个表达形式为 所以,Cn是一个自然数;这一点
在先前的通项公式中并不显而易见。这个表达形式也是André对前一公式证明的基础。
递推关系
它也满足
- //这个在本题中用来推导卡特兰数!
- 很重要的一个推导式!!
这提供了一个更快速的方法来计算卡塔兰数。
卡塔兰数的渐近增长为
它的含义是左式除以右式的商趋向于1当n → ∞。(这可以用n!的斯特灵公式来证明。)
所有的奇卡塔兰数Cn都满足。所有其他的卡塔兰数都是偶数。
卡特兰数的应用:
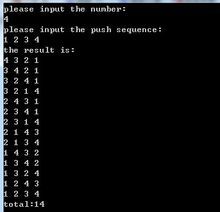
出栈次序
一个 栈 (无穷大)的 进栈 序列为1,2,3,…,n,有多少个不同的 出栈 序列?
个是k+1~n,序列个数是n-k。
此时,我们若把k视为确定一个序数,那么根据乘法原理,f(n)的问题就等价于——序列个
数为k-1的出栈序列种数乘以
序列个数为n - k的出栈序列种数,即选择k这个序数的f(n)=f(k-1)
×f(n-k)。而k可以选1到n,所以再根据加法原理,将k
取不同值的序列种数相加,得到的总序列种数为:f(n)=f(0)f(n-1)
+f(1)f(n-2)+……+f(n-1)f(0)。
看到此处,再看看卡特兰数的递推式,答案不言而喻,即为f(n)=h(n)
= C(2n,n)/(n+1)=
c(2n,n)-c(2n,n+1)(n=1,2,3,……)。
最后,令f(0)=1,f(1)=1。
非常规分析
对于每一个数来说,必须进栈一次、出栈一次。我们把进栈设为状态‘1’,出栈
设为状态‘0’。n个数的所有状态对应n个1
和n个0组成的2n位二进制数。由于等待入
栈的操作数按照1‥n的顺序排列、入栈的
操作数b大于等于出栈的操作数a(a≤b),
因此输出序列的总数目=由左而右扫描由n个1和n个0组成的2n位二进制数,1的累计
数不小于0的累计数的方案种数。
在2n位二进制数中填入n个1的方案数为c(2n,n),不填1的其余n位自动填0。从中
减去不符合要求(由左而右扫描,0的累
计数大于1的累计数)的方案数即为所求。
不符合要求的数的特征是由左而右扫描时,必然在某一奇数位2m+1位上首先出
现m+1个0的累计数和m个1的累计数,此
后的2(n-m)-1位上有n-m个 1和n-m-1个0。
如若把后面这2(n-m)-1位上的0和1互换,
使之成为n-m个0和n-m-1个1,结果得1
个由n+1个0和n-1个1组成的2n位数,即一个不合要求的数对应于一个由n+1个0和
n-1个1组成的排列。
反过来,任何一个由n+1个0和n-1个1组成的2n位二进制数,由于0的个数多2个
,2n为偶数,故必在某一个奇数位上出
现0的累计数超过1的累计数。同样在后面部分
0和1互换,使之成为由n个0和n个1组
成的2n位数,即n+1个0和n-1个1组成的
2n位数
必对应一个不符合要求的数。
因而不合要求的2n位数与n+1个0,n-1个1组成的排列一一对应。
显然,不符合要求的方案数为c(2n,n+1)。由此得出输出序列的总数目=c(2n,n)-c(2n,n+1)
=c(2n,n)/(n+1)=h(n+1)。
类似问题 买票找零
有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票,另外n人
只有10元钞票,剧院无其它钞票
,问有多少中方法使得只要有10元的人买票,售票处就有
5元的钞票找零?(将持5元者到
达视作将5元入栈,持10元者到达
视作使栈中某5元出栈)
凸多边形三角划分
在一个 凸多边形 中,通过若干条互不相交的对角线,把这个多边形划分成了若
干个 三角形
。现在的任务是键盘上输入
凸多边形的边数n,求不同划分的方案数f(n)。
比如当n=6时,f(6)=14。
[6]
,恐怕很难找到问题的递推式,我们必须
从一般情况出发去找规律。
因为凸多边形的任意一条边必定属于某一个三角形,所以我们以某一条边为
基准,以这条边的两个顶点为起点P1和终
点Pn(P即Point),将该凸多边形的顶
点依序标记为P1、P2、……、Pn,再在
该凸多边形中找任意一个不属于这两个点
的顶点Pk(2<=k<=n-1),来构成一个三角形,用这个三角形把一个凸多边形
划分成两个凸多边形,其中一个凸多边形,
是由P1,P2,……,Pk构成的凸k边形
(顶点数即是边数),另一个凸多边形
,是由Pk,Pk+1,……,Pn构成的凸n-k+1
边形。
此时,我们若把Pk视为确定一点,那么根据乘法原理,f(n)的问题就等
价于——凸k多边形的划分方案数乘以凸n-k+1
多边形的划分方案数,即选择Pk
这个顶点的f(n)=f(k)×f(n-k+1)。而k可
以选2到n-1,所以再根据加法原理,
将k取不
同值的划分方案相加,得到的总方案数为:f(n)=f(2)f(n-2+1)
+f(3)f(n-3+1)+……+f(n-1)f(2)。看到此处,
再看看卡特兰数的递推式,答案不言而喻,即为f(n)=h(n-1)
(n=2,3,4,……)。
最后,令f(2)=1,f(3)=1。
此处f(2)=1和f(3)=1的具体缘由须参考详尽的“卡特兰数”,也许可从
凸四边形f(4)=f(2)f(3)+ f(3)f(2)=
2×f(2)f(3)倒推,四边形的
划分方案不用规律推导都可以知道是2,那么
2×f(2)f(3)=2,则f(2)f(3)=1,又f(2)
和f(3)若存在的话一定是整数,
则f(2)=1,f(3)=1。
(因为我没研究过卡特兰数的由来,此处仅作刘抟羽的臆测)。
…………
2.在c以及c++中,EOF被定义成-1!
3.如何处理大数的乘除法!很妙的方法!参考代码!
代码如下:
//输出卡特兰数
//首先需要肯定,程序是正确的
//这算是大数乘除法!记住他们是如何处理的!由于数据很大,用基本数据类型根本无法满足要求,只能用数组来表示!
#include <iostream>
#include<cstdio>
#include<memory.h>
using namespace std;
#define MAX 101
#define BASE 10000//base只是一个基度,对最终取值并没有影响,相反,base取值愈大,计算量愈小
//base发生改变的时候,下面的输出也要相应地做出调整,否则也会输出错误答案!除非当base取10!
void multiply(int a[],int len,int b)//乘法
{
for(int i=len-1,carry=0;i>=0;--i)//从最后一位开始相乘,依次向前与每一位相乘
{//问题在于,为什么BASE=10000?
carry+=b*a[i];
a[i]=carry%BASE;
carry/=BASE;
//cout<<"carry="<<carry<<" "<<"a["<<i<<"]="<<a[i]<<endl;//以4个0为一组
}
}
void divide(int a[],int len,int b)//除法,很妙的!这种除法可能想不到,仔细体会!
{//应当如何除呢?
for(int i=0,div=0;i<len;++i)//从高位除起
{
div=div*BASE+a[i];
a[i]=div/b;//b为除数
div%=b;
}
}
int main()
{
int i,j,h[101][MAX];
memset(h[1],0,MAX*sizeof(int));//赋值,每一个都置为0
for(i=2,h[1][MAX-1]=1;i<=100;++i)//运用递归,并且h[1]=1;
{
memcpy(h[i],h[i-1],MAX*sizeof(int));//h[i]=h[i-1];按字节拷贝,保证了h[i]和h[i-1]指向数组的一致性
multiply(h[i],MAX,4*i-2);//h[i]*=(4*i-2);
divide(h[i],MAX,i+1);//h[i]/=(i+1);
}//递归得到前100项的卡特兰数!
while(cin>>i && i>=1 && i<=100)//输入i的值
{
// for(i=1;i<=100;i++)
// {
for(j=0;j<MAX && h[i][j]==0;++j);//从0位开始搜索,找到不为0的第一个数
//printf("%d\n",EOF);在c语言中,EOF=-1;
printf("%d",h[i][j++]);//像是这个输出,就很妙了,第一位可能不足四位,就地输出!
for(;j<MAX;++j)
{
// if(h[i][j]==0)
printf("%04d",h[i][j]);//处在中间的值也可能没有四位,这时候要注意了,往左边加0,凑足4位,不然答案会出错!
// else
// printf("%d",h[i][j]);//不断输出值
}
printf("\n");
}
system("pause");
return 0;
}
