决定系数和残差
首先看看几个定义:
总体平方和TSS( total sum of squares)
回归平方和RSS(regression sum of squares)
残差平方和ESS(Residual sum of squares)
其中,yi表示实验数据,fi 表示模拟值,![]() 表示样本平均值。
表示样本平均值。
决定系数(Coefficient of determination)
在一定程度上反应了模型的拟合优度。
其实就是回归平方和在总体平方和中所占的比例。因为TSS=RSS+ESS
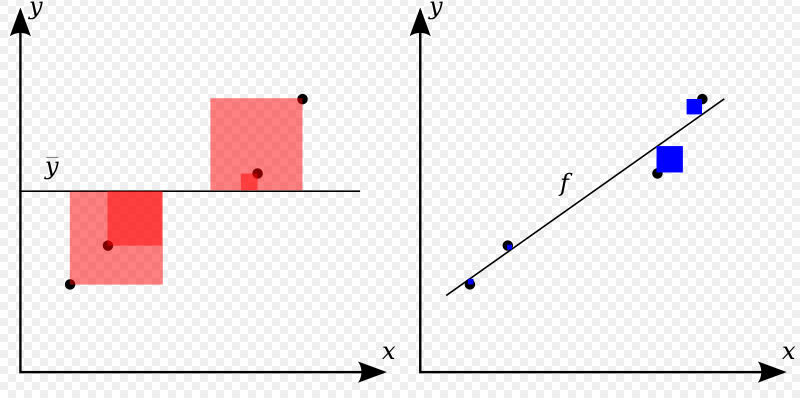
The better the linear regression (on the right) fits the data in comparison to the simple average (on the left graph), the closer the value of R2 is to one. The areas of the blue squares represent the squared residuals with respect to the linear regression. The areas of the red squares represent the squared residuals with respect to the average value.
红色区域是总体平方和,蓝色为残差平方和。
>> 为什么要用决定系数去反应拟合优度,而不用残差平方和呢?
>> 因为,残差平方和与观测值的绝对大小有关,而决定系数是一个比例。
比如:有一组数据:1000,2000,35000...
另一组数据:1,2,3.5...
这个时候就会发现第一组数据的拟合后残差平方和会大很多,但是不见得,模型拟合优度就会差。
see also: wikipedia