【每日算法】图算法（遍历&MST&最短路径&拓扑排序）

图有邻接矩阵和邻接表两种存储方法，邻接矩阵很简单，这里不讨论，下面我们先看看常用的邻接表表示方法。

邻接表常用表示方法

指针表示法

指针表示法一共需要两个结构体：

struct ArcNode  //定义边表结点 
{
    int adjvex； //邻接点域
    ArcNode* next;
};

struct VertexNode   //定义顶点表结点
{
    int vertex;
    ArcNode* firstedge;
};

每个节点对应一个VertexNode，其firstedge指向边表（与当前节点邻接的表构成的链表）的头节点。

vector表示法

使用vector模拟邻接表，十分方便简洁，v是一个数组，对应于上面的顶点表，v[i]是一个vector，存放邻接顶点的下标。
这种方法的缺陷是：要求顶点的编号从0~MAXN-1。

vector<int> v[MAXN];

数组表示法

head[i]：指向编号为i的顶点的邻接表中第一条边的序号；
h：边的序号；
e：边表，每条边对应一个序号，由h给出；

int head[MAXN]; //初始化为-1
int h = 0;

struct Edge
{
    int adjvex;
    int next;
};

Edge e[MAXN<<1]；

void add(int a, int b) //a与b邻接
{
    e[h].adjvex = b; //当前边的序号为h，
    e[h].next = head[a]; //头插法
    head[a] = h++;
}

深度优先遍历

图的深度优先遍历（DFS）类似于树的前序遍历：

访问顶点v，visited[v] = 1;
w = 顶点v的第一个邻接点；
while(w存在)
    if(w未被访问) 从顶点w出发递归执行DFS；
    w = 顶点v的下一个邻接点；

广度优先遍历

图的广度优先遍历（BFS）类似于树的层次遍历：

初始化队列Q；
访问顶点v；visited[v] = 1；顶点v入队列Q；
while(队列非空)
    v = 队列Q的队头元素出队；
    w = 顶点v的第一个邻接点；
    while (w存在)
        如果w未被访问，访问w；visited[w] = 1;顶点w入队列Q；
        w = 顶点v的下一个邻接点；

注意，我们这里的队列用来存储已被访问的顶点，即对于每个顶点，我们是先访问，再入队，这样可以避免顶点的重复入队。

最小生成树（MST）

最小生成树算法以Prim算法和Kruskal算法最为经典。

Prim算法

初始化：一个顶点，空边集。

其基本思想是，寻找这样的边：满足“一个点在生成树中，一个点不在生成树中”的边中权值最小的一条边。将找到的边加入边集中，顶点加到顶点集中，当所有顶点都加入进来时，算法结束。

初始化: U = {v0}; TE = {};
while (U != V)
{ 在E中寻找最短边(u, v),且满足 u∈U，v∈V-U； U = U + {v}；
    TE = TE + {(u, v)};
}

由于Prim需要不断读取任意两个顶点之间边的权值，所以适合用邻接矩阵存储。

为找出最短边，我们定义一个候选最短边的集合，用来存放候选的边（一个点在生成树中，一个点不在生成树中）。我们使用数组shortEdge[n]来表示这个集合，数组元素包含adjvex和lowcost两个域，分别表示邻接点和权值。比如shortEdge[i].adjvex = k, shrotEdge[i].lowcost = w表示下标为i和下标为k的顶点邻接，边的权值为w。

void Prim(Graph G)
{
    for (int i = 1; i < G.vertexNum; ++i) //初始化辅助数组
    {
        shortEdge[i].lowcost = G.arc[0][i];
        shortEdge[i].adjvex = 0;
    }
    shortEdge[0].lowcost = 0; //将顶点0加入集合U
    for (int i = 1; i < G.vertexNum; ++i)
    {
        int k = MinEdge(shortEdge, G.vertexNum); //寻找最短边的邻接点k；
        cout << '(' << k << ',' << shortEdge[k].adjvex << ')' << endl;
        shorEdge[k].lowcost = 0; //将k加入集合U
        for (int j = 1; j < G.vertexNum; ++j) //更新数组shortEdge
        {
            //k新加入U，更新与k邻接的点的lowcost。
            if (G.arc[k][j] < shortEdge[j].lowcost)
            {
                shortEdge[j].lowcost = G.arc[k][j];
                shortEdge[j].adjvex = k;
            }
        }
    }
}

Prim算法的时间复杂度为O(n^2)，与图中的边数无关，适合求稠密图的最小生成树。

Kruskal算法

初始化：n个顶点（即n个连通分量），空边集。

其基本思想是：每次从未标记的边中选取最小权值的边，如果该边的两个顶点位于两个不同的连通分量，则将该边加入最小生成树，合并两个连通分量，并标记该边。否则，位于同一个连通分量，则去掉该边（同样标记即可），避免造成回路。

可见，此算法的关键是：如何考察两个顶点是否位于两个不同连通分量。最简单的做法是：使用并查集。

此算法需要对边进行操作，所以我们用边集数组存储图的边，为提高最短边查找速度，可以先按权值排序。

const int MaxVertex = 10;
const int MaxEdge = 100;
struct EdgeType
{
    int from, to;
    int weight;
};

template <class DataType>
struct EdgeGraph
{
    DataType vertex[MaxVertex];
    EdgeType edge[MaxEdge];
    int vertexNum, edgeNum;
};

void Kruskal(EdgeGraph G)
{
    for (int i = 0; i < G.vertexNum; ++i)
        parent[i] = -1;
    for (int num = 0, i = 0; i < G.edgeNum; ++i)
    {
        v1 = FindRoot(partent, G.edge[i].from);
        v2 = FindRoot(partent, G.edge[i].to);
        if (v1 != v2) //不同连通分量
        {
            cout << '(' << v1 << ',' << v2 << ')' << endl;
            parent[v2] = v1; //合并
            num++;
            if (num == n-1) return;
        }
    }
}

int FindRoot(int parent[], int v)
{
    int t = v;
    if (parent[t] != -1) t= parent[t]; //一直往上找到根节点
    return t;
}

最短路径

最短路径经典的算法有Dijkstra算法（单源最短路，不能处理负权），SPFA算法（单源最短路，可处理负权），Floyd算法（任一对顶点间的最短路）。

Dijkstra算法

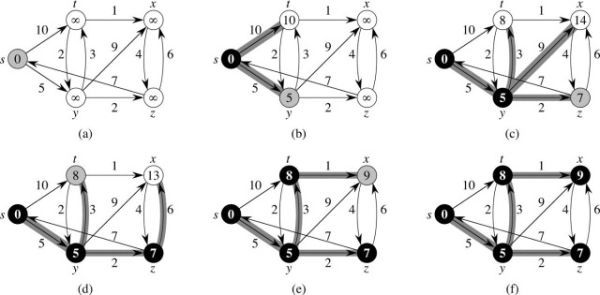
此算法使用贪心策略，这里作为复习，只讲一讲实现，不再讨论原理了，下面贴出一张图，方便大家回忆。

其中黑色顶点之间的灰色边为已选的边，黑色与灰色顶点之间的灰色边为候选边。

每一次添加一条边就更新顶点的最短路径值，贪心策略为每次选取值最小的点。

由于此算法需要快速求得任意两顶点之间边的权值，所以用邻接矩阵存储。

为记录每个顶点的最短路径值，需要辅助数组dist[n]：dist[i]表示当前所找到的从源点v到终点vi的最短路径长度。
初始值：若从v到vi有弧，则dist[i]为弧上的权值，否则为正无穷。

为记录路径，需要辅助数组path[n]：path[i]为一个字符串，表示当前所找到的从源点v到终点vi的最短路径。
初始值：若从v到vi有弧，则path[i]为“v vi”，否则为“”。

数组s[n]：存放源点和已经生成的终点。

伪代码：

初始化数组dist，path和s
while (s中元素个数 < n)
{
    在dist[n]中找最小值，其编号为k；
    输出dist[k]和path[k]；
    修改数组dist和path；
    将顶点k添加到数组s中；
}

C++实现：

void Dijkstra(MGraph G, int v)
{
    for (int i = 0; i < G.vertexNum; ++i)
    {
        s[i] = 1;
        dist[i] = G.arc[v][i];
        if (path[i] != INF)
            path[i] = G.vertex[v]+G.vertex[i];
        else
            path[i] = "";
    }
    s[v] = 0; //将源点加入集合S中
    dist[v] = 0;
    int num = 1;
    while (num < G.vertexNum)
    {
        int k = 0;
        for (int i = 0; i < G.vertexNum; ++i)
            if (s[i] && (dist[i] < dist[k]))
                k = i;
        cout << dist[k] << ' ' << path[k] <<endl;
        s[k] = 0;
        ++num;
        for (int i = 0; i < G.vertexNum; ++i)
            if (dist[i] > dist[k] + G.arc[k][i])
            {
                dist[i] = dist[k] + G.arc[k][i];
                path[i] = path[k] + G.vertex[i];
            }
    }
}

时间复杂度为O(n^2)。

Floyd算法

Floyd算法用于求每一对顶点之间的最短路径问题，其算法复杂度为O(n^3)。

void Floyd(MGraph G)
{
    for (int i = 0; i < G.vertexNum; ++i)
        for (int j = 0; j < G.vertexNum; ++j)
        {
            dist[i][j] = G.arc[i][j];
            if (dist[i][j] != INF)
                path[i][j] = G.vertex[i]+G.vertex[j];
            else
                path[i][j] = "";
        }
    for (int k = 0; k < G.vertexNum; ++k)
        for (int i = 0; i < G.vertexNum; ++i)
            for (int j = 0; j < G.vertexNum; ++j)
            {
                if (dist[i][k]+dist[k][j] < dist[i][j])
                {
                    dist[i][j] = dist[i][k]+dist[k][j];
                    path[i][j] = path[i][k] + path[k][j];
                }
            }
}

注意k要放在最外层，因为dist[i][j] 依赖于 dist[i][k]和dist[k][j]， 所以k小的需要先计算。

SPFA

SPFA（Shortest Path Faster Algorithm）（队列优化）算法是求单源最短路径的一种算法，它还有一个重要的功能是判负环（在差分约束系统中会得以体现），在Bellman-ford算法的基础上加上一个队列优化，减少了冗余的松弛操作，是一种高效的最短路算法。

bool SPFA(MGraph G, int s)
{
    for (int i = 0; i < G.vertexNum; ++i)
    {
        dist[i] = G.arc[v][i];
    }
    dist[v] = 0;
    memset(vis, 0, sizeof(vis));
    deque<int> q;
    q.push_back(s);
    vis[s] = true;
    while (!q.empty())
    {
        int k = q.front();
        q.pop_front();
        vis[k] = false;
        for (int i = 0; i < G.vertexNum; ++i)//存在负权的话，就需要创建一个COUNT数组，当某点的入队次数超过vertexNum(顶点数)返回。
        {
            if (dist[i] > dist[k] + G.arc[k][i])
            {
                dist[i] = dist[k] + G.arc[k][i];
                if (!vis[i])
                {
                    q.push_back(i);
                    vis[i] = true;
                }
            }
        }
    }
}

拓扑排序

参加另一篇博文：

拓扑排序算法的实现——Kahn算法及基于dfs的算法

结语

从前阵子开始，我就打算好好梳理一下学过的基础算法，一来为接下来的面试做准备，二来可以跟大家分享自己学到的知识。

近期比较忙，所以说好的【每日算法】没能做到每日更新。

今天匆匆忙忙将几个图算法回顾了一遍，上面的代码也大多数是伪代码，或者是用C++实现的大体思路（没有经过测试，请见谅！）。

接下来可能暂时停更，等到过阵子忙完再好好写几篇质量高一点的博文～

每天进步一点点，Come on！

(●’◡’●)

本人水平有限，如文章内容有错漏之处，敬请各位读者指出，谢谢！