【机器学习】迭代决策树GBRT（渐进梯度回归树）

一、决策树模型组合

        单决策树C4.5由于功能太简单，并且非常容易出现过拟合的现象，于是引申出了许多变种决策树，就是将单决策树进行模型组合，形成多决策树，比较典型的就是迭代决策树GBRT和随机森林RF。

        在最近几年的paper上，如iccv这种重量级会议，iccv 09年的里面有不少文章都是与Boosting和随机森林相关的。模型组合+决策树相关算法有两种比较基本的形式：随机森林RF与GBDT，其他比较新的模型组合+决策树算法都是来自这两种算法的延伸。

       核心思想：其实很多“渐进梯度”Gradient Boost都只是一个框架，里面可以套用很多不同的算法。

 

        首先说明一下，GBRT这个算法有很多名字，但都是同一个算法：

GBRT (Gradient BoostRegression Tree) 渐进梯度回归树

GBDT (Gradient BoostDecision Tree) 渐进梯度决策树

MART (MultipleAdditive Regression Tree) 多决策回归树

Tree Net决策树网络

代码示例：该版本发布在了google code上：http://code.google.com/p/simple-gbdt/

 

二、GBRT

        迭代决策树算法，在阿里内部用得比较多（所以阿里算法岗位面试时可能会问到），由多棵决策树组成，所有树的输出结果累加起来就是最终答案。它在被提出之初就和SVM一起被认为是泛化能力（generalization)较强的算法。近些年更因为被用于搜索排序的机器学习模型而引起大家关注。

        GBRT是回归树，不是分类树。其核心就在于，每一棵树是从之前所有树的残差中来学习的。为了防止过拟合，和Adaboosting一样，也加入了boosting这一项。

　　关于GBRT的介绍可以可以参考：GBDT（MART） 迭代决策树入门教程 | 简介。

 

        提起决策树（DT, DecisionTree）不要只想到C4.5单分类决策树，GBRT不是分类树而是回归树！

决策树分为回归树和分类树：

        回归树用于预测实数值，如明天温度、用户年龄

        分类树用于分类标签值，如晴天/阴天/雾/雨、用户性别

        注意前者结果加减是有意义的，如10岁+5岁-3岁=12岁，后者结果加减无意义，如男+女=到底是男还是女？GBRT的核心在于累加所有树的结果作为最终结果，而分类树是没有办法累加的。所以GBDT中的树都是回归树而非分类树。

 

        第一棵树是正常的，之后所有的树的决策全是由残差（此次的值与上次的值之差）来作决策。

 

三、算法原理

0.给定一个初始值

1.建立M棵决策树（迭代M次）

2.对函数估计值F(x)进行Logistic变换

3.对于K各分类进行下面的操作（其实这个for循环也可以理解为向量的操作，每个样本点xi都对应了K种可能的分类yi，所以yi，F(xi)，p(xi)都是一个K维向量）

4.求得残差减少的梯度方向

5.根据每个样本点x，与其残差减少的梯度方向，得到一棵由J个叶子节点组成的决策树

6.当决策树建立完成后，通过这个公式，可以得到每个叶子节点的增益（这个增益在预测时候用的）

       每个增益的组成其实也是一个K维向量，表示如果在决策树预测的过程中，如果某个样本点掉入了这个叶子节点，则其对应的K个分类的值是多少。比如GBDT得到了三棵决策树，一个样本点在预测的时候，也会掉入3个叶子节点上，其增益分别为（假设为3分类问题）：

(0.5, 0.8, 0.1), (0.2, 0.6, 0.3), (0.4, .0.3, 0.3)，那么这样最终得到的分类为第二个，因为选择分类2的决策树是最多的。

7.将当前得到的决策树与之前的那些决策树合并起来，作为一个新的模型（跟6中的例子差不多）

 

--------------------------------------------------------------------------------------------------------------

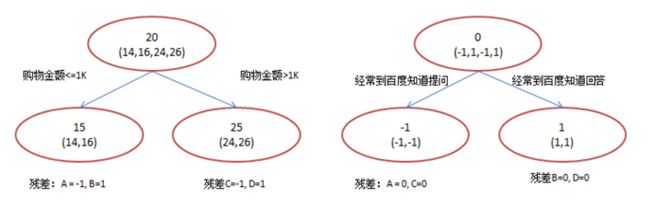
        还是年龄预测，简单起见训练集只有4个人，A,B,C,D，他们的年龄分别是14,16,24,26。其中A、B分别是高一和高三学生；C,D分别是应届毕业生和工作两年的员工。如果是用一棵传统的回归决策树来训练，会得到如下图1所示结果：

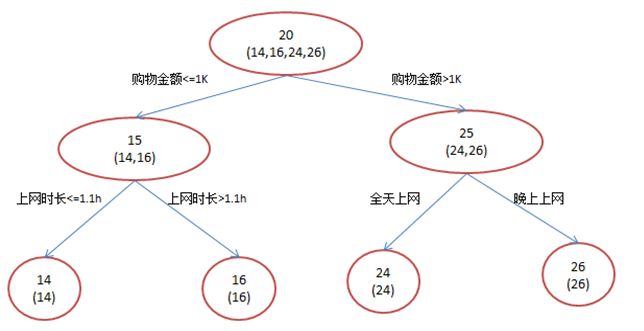
        现在我们使用GBDT来做这件事，由于数据太少，我们限定叶子节点做多有两个，即每棵树只有一个分枝，并且限定只学两棵树。我们会得到如下图2所示结果： 

        在第一棵树分枝和图1一样，由于A,B年龄较为相近，C,D年龄较为相近，他们被分为两拨，每拨用平均年龄作为预测值。此时计算残差（残差的意思就是： A的预测值 + A的残差 = A的实际值），所以A的残差就是16-15=1（注意，A的预测值是指前面所有树累加的和，这里前面只有一棵树所以直接是15，如果还有树则需要都累加起来作为A的预测值）。进而得到A,B,C,D的残差分别为-1,1，-1,1。然后我们拿残差替代A,B,C,D的原值，到第二棵树去学习，如果我们的预测值和它们的残差相等，则只需把第二棵树的结论累加到第一棵树上就能得到真实年龄了。这里的数据显然是我可以做的，第二棵树只有两个值1和-1，直接分成两个节点。此时所有人的残差都是0，即每个人都得到了真实的预测值。 

        换句话说，现在A,B,C,D的预测值都和真实年龄一致了。

A: 14岁高一学生，购物较少，经常问学长问题；预测年龄A = 15 – 1 = 14

B: 16岁高三学生；购物较少，经常被学弟问问题；预测年龄B = 15 + 1 = 16

C: 24岁应届毕业生；购物较多，经常问师兄问题；预测年龄C = 25 – 1 = 24

D: 26岁工作两年员工；购物较多，经常被师弟问问题；预测年龄D = 25 + 1 = 26  

        那么哪里体现了Gradient呢？其实回到第一棵树结束时想一想，无论此时的cost function是什么，是均方差还是均差，只要它以误差作为衡量标准，残差向量(-1, 1, -1, 1)都是它的全局最优方向，这就是Gradient。 

四、GBRT适用范围

        该版本的GBRT几乎可用于所有的回归问题（线性/非线性），相对logistic regression仅能用于线性回归，GBRT的适用面非常广。亦可用于二分类问题（设定阈值，大于阈值为正例，反之为负例）。

 

五、搜索引擎排序应用RankNet

        搜索排序关注各个doc的顺序而不是绝对值，所以需要一个新的cost function，而RankNet基本就是在定义这个cost function，它可以兼容不同的算法（GBDT、神经网络...）。

        实际的搜索排序使用的是Lambda MART算法，必须指出的是由于这里要使用排序需要的cost function，LambdaMART迭代用的并不是残差。Lambda在这里充当替代残差的计算方法，它使用了一种类似Gradient*步长模拟残差的方法。这里的MART在求解方法上和之前说的残差略有不同，其区别描述见这里。

         搜索排序也需要训练集，但多数用人工标注实现，即对每个(query, doc)pair给定一个分值（如1, 2, 3, 4），分值越高越相关，越应该排到前面。RankNet就是基于此制定了一个学习误差衡量方法，即cost function。RankNet对任意两个文档A,B，通过它们的人工标注分差，用sigmoid函数估计两者顺序和逆序的概率P1。然后同理用机器学习到的分差计算概率P2（sigmoid的好处在于它允许机器学习得到的分值是任意实数值，只要它们的分差和标准分的分差一致，P2就趋近于P1）。这时利用P1和P2求的两者的交叉熵，该交叉熵就是cost function。

        有了cost function，可以求导求Gradient，Gradient即每个文档得分的一个下降方向组成的N维向量，N为文档个数（应该说是query-doc pair个数）。这里仅仅是把”求残差“的逻辑替换为”求梯度“。每个样本通过Shrinkage累加都会得到一个最终得分，直接按分数从大到小排序就可以了。

推荐到极客头条

http://blog.csdn.net/dianacody/article/details/40688783