机器学习算法-决策树理论
用较少的东西,同样可以做好的事情。越是小的决策树,越优于大的决策树。
引文
数据分类是一个两阶段过程,包括学习阶段(构建分类模型)和分类阶段(使用模型预测给定数据的类标号)。决策树分类算法是监督学习的一种,即Supervised learning。
- 分类过程的第一阶段也可以看做学习一个映射或函数y=f(x),它可以预测给定元组X的类标号y。
- 在第二阶段,使用模型进行分类。首先评估分类器的预测准确率。这个过程要尽量的减少过拟合。(为什么是尽量减少而不是避免呢,因为过拟合一般是避免不了的,再好的模型也会有过拟合的情况)。
1 决策树归纳
决策树归纳是从有类标号的训练元组中学习决策树。常用的决策树算法有ID3,C4.5和CART。它们都是采用贪心(即非回溯的)方法,其中决策树自顶向下递归的分治方法构造。其中划分属性的方法各不相同,ID3使用的是信息增益,C4.5使用的是信息增益率,而CART使用的是Gini基尼指数。下面来简单介绍下决策树的理论知识。内容包含熵、信息增益、信息增益率以及Gini指数的计算公式。
2 基本原理
2.1 算法优点
决策树算法的优点如下:
(1)分类精度高;
(2)成的模式简单;
(3)对噪声数据有很好的健壮性。
因而是目前应用最为广泛的归纳推理算法之一,在数据挖掘中受到研究者的广泛关注。
2.2 算法一般流程
(1)收集数据:任意方法和途径。
(2)准备数据:书构造算法只适用于标称型数据,因此数据必须离散化。
(3)分析数据:构造树完成后,检查图形是否符合预测。
(4)训练算法:决策树的数据构造。
(5)测试算法:一般将决策树用于分类,可以用错误率衡量,而错误率使用经验率计算。
(6)使用算法:决策树可以用于任何监督学习算法。
2.3 实例
信息增益和熵(克劳德.香农提出)
1.使用信息增益进行决策树归纳
信息增益度量属性选择
熵(Entropy)的计算公式
熵定义为信息增益的期望值。熵越大,一个变量的不确定性就越大(也就是可取的值很多),把它分析清楚需要的信息量也就越大,熵是整个系统的平均信息量。对 D 中的元组分类所需要的期望信息由下列公式给出:
熵越大,说明系统越混乱,携带的信息就越少。熵越小,说明系统越有序,携带的信息就越多。信息的作用就是在于消除不确定性。
ID3划分特征使用的就是信息增益IG.
一个属性的信息增益越大,表明属性对样本的熵减少的能力就更强,该属性使得数据所属类别的不确定性变为确定性的能力越强。
注:需要的期望信息越小,分区的纯度越高。
信息增益计算
首先计算特征A对数据集D的经验条件熵 H(D|A) ,在数学上就是条件概率分布(Condition Probability)
引入条件熵,在信息论中主要是为了消除结果的不确定性。
然后计算信息增益
其中, Gain(A) 即为所求的信息增益。
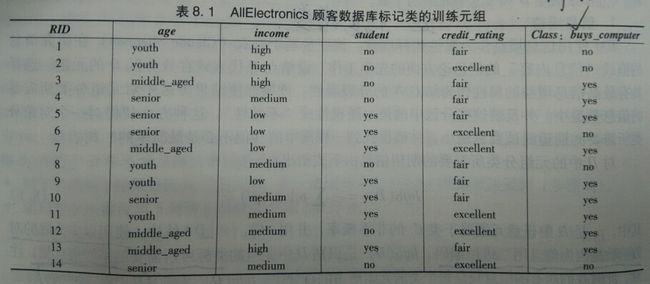
下面来应用一个实例,训练元组数据D
在这里
根据计算出来的条件熵,计算按 age 划分的信息增益,计算方法如下:
类似的可以计算出其它属性的信息增益:
由于 age 在属性中具有最高的信息增益,所以它被选作分裂特征。下面再进行递归计算信息增益,在此就不展示了。
ID3采用的就是就是IG,算法步骤如下:


2.使用增益率计算
ID3使用的是信息增益,C4.5使用的是信息增益率。
C4.5算法继承了ID3算法的优点,并在以下几方面对ID3算法进行了改进:
1) 用信息增益率来选择属性,克服了用信息增益选择属性时偏向选择取值多的属性的不足;
2) 在树构造过程中进行剪枝;
3) 能够完成对连续属性的离散化处理;
4) 能够对不完整数据进行处理。
C4.5算法有如下优点:产生的分类规则易于理解,准确率较高。其缺点是:在构造树的过程中,需要对数据集进行多次的顺序扫描和排序,因而导致算法的低效。此外,C4.5只适合于能够驻留于内存的数据集,当训练集大得无法在内存容纳时程序无法运行。
另外,无论是ID3还是C4.5最好在小数据集上使用,决策树分类一般只试用于小数据。当属性取值很多时最好选择C4.5算法,ID3得出的效果会非常差。
分裂信息计算公式:
增益率定义为:
选择具有最大增益率的特征作为分裂特征。
3.基尼指数Gini index
基尼指数在CART中使用,Gini index度量的是数据分区或训练元组集D的不纯度。计算方式如下:
3.学习推介
Andrew W. Moore PPT dtree
决策树Python实现,单独成文,网址:决策树实现
Wikipedia维基百科-Decision Tree决策树
最后,附一张决策树的优点和缺点图:
4.Reference
[1]数据挖掘概念与技术 Third Edition,韩家伟.
[2]机器学习实战 ,Peter Harrington.