CF286D/bzoj-4223 Tourists

题意：

直角坐标系下，在一些时刻会有两个游客分别同时从点 (−1, 0) 和 (1, 0) 出发；

每一对游客每秒都向 y 轴正方向前进一个单位长度；

在一些时刻墙会出现，墙 (li,ri) 是一条在点 (0,li) 和(0,ri) 之间的线段；

给出 m 堵墙的出现时间 ti 以及出现的区间，给出 n 对游客出发时间 qi；

请求出对于每一对游客有多长时间无法彼此望见。

n，m<=10^5，li,ri,ti<=10^9；

UPD：发现了在大视野的双倍经验！

题解：
自己YY不动这个扫描线，所以去vfk的题解里膜了一个扫描线姿势；

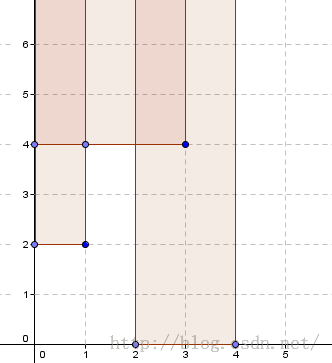
因为墙出现了就不再消失，所以考虑将墙的li,ri看成纵坐标，将时间看成横坐标，那么就得到了一个没有上界的矩形；

而多个墙并起来就是一个无上界的奇怪图形，我们要处理出这个图形的所有顶点；

(此图及以下图片都是样例2)

处理的方法就是用一个堆维护当前扫到的所有点中时间的最小值，然后从左往右扫，扫到一个边在边界上的边就处理一下什么的；

这个点数目显然不会太多，最多在m*4的级别；

为了方便处理我在最上面(0x7f7f7f7f)加了一个长条矩形作为边界，但是注意这个要足够高，0x3f3f3f3f会挂；

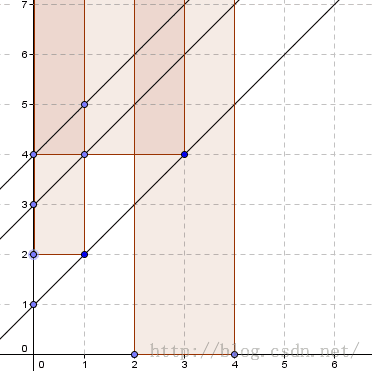
处理了所有的点之后，对于时间pi出发的旅客，答案就是直线y=x+pi在这个图形上截的x轴距离；

正确性YY一下还是显然的，然后从右下向左上用一条y=x的直线扫并计算答案就可以了；

算法过程中只需要记录now当前的答案，以及cnt当前可以增长答案的线段个数；

每次经过询问就更新答案，经过端点时更改线段个数；

这些扫描的时间复杂度都是线性的，然而排序是O(nlogn)哦。。。

代码：

#include<queue>
#include<stdio.h>
#include<string.h>
#include<algorithm>
#define N 110000
#define pr pair<int,int>
using namespace std;
struct wall
{
	int no,x,t;
	friend bool operator <(wall a,wall b)
	{
		if(a.x!=b.x)
			return a.x<b.x;
		return a.t<b.t;
	}
}w[N<<1];
struct Point
{
	int x,y,type,no;
	friend bool operator <(Point a,Point b)
	{
		return a.y-a.x<b.y-b.x;
	}
}p[N*5];
int tot;
int L[N],R[N],T[N];
priority_queue<pr,vector<pr>,greater<pr> >q;
bool vis[N];
int ans[N];
int main()
{
	int n,m,i,k,now,cnt;
	scanf("%d%d",&m,&n);
	for(i=1;i<=n;i++)
	{
		scanf("%d%d%d",L+i,R+i,T+i);
		w[i<<1].no=w[i<<1|1].no=i;
		w[i<<1].x=L[i],w[i<<1|1].x=R[i];
		w[i<<1].t=w[i<<1|1].t=T[i];
	}
	sort(w+2,w+n+n+2);
	q.push(pr(0x7f7f7f7f,0));
	vis[0]=1;
	for(i=2;i<=n+n+1;i++)
	{
		if(!vis[w[i].no])
		{
			while(!q.empty()&&!vis[q.top().second])
				q.pop();
			if(!q.empty()&&w[i].t<q.top().first)
			{
				tot++;
				p[tot].x=w[i].x;
				p[tot].y=q.top().first;
				p[tot].type=1;
				tot++;
				p[tot].x=w[i].x;
				p[tot].y=w[i].t;
				p[tot].type=-1;
			}
			q.push(pr(w[i].t,w[i].no));
			vis[w[i].no]=1;
		}
		else
		{
			while(!q.empty()&&!vis[q.top().second])
				q.pop();
			if(q.top().second==w[i].no)
			{
				q.pop();
				while(!q.empty()&&!vis[q.top().second])
					q.pop();
				tot++;
				p[tot].x=w[i].x;
				p[tot].y=w[i].t;
				p[tot].type=1;
				tot++;
				p[tot].x=w[i].x;
				p[tot].y=q.top().first;
				p[tot].type=-1;
			}
			vis[w[i].no]=0;
		}
	}
	for(i=1;i<=m;i++)
	{
		scanf("%d",&k);
		tot++;
		p[tot].type=0;
		p[tot].x=0;
		p[tot].y=k;
		p[tot].no=i;
	}
	sort(p+1,p+tot+1);
	for(i=1,now=0,cnt=0;i<=tot;i++)
	{
		now+=cnt*(p[i].y-p[i].x-p[i-1].y+p[i-1].x);
		cnt+=p[i].type;
		if(!p[i].type)
			ans[p[i].no]=now;
	}
	for(i=1;i<=m;i++)
		printf("%d\n",ans[i]);
	return 0;
}