数据结构-二叉树和二叉查找树
先按树-二叉树-二叉查找树的顺序解释会比较清楚。
一,树
树(Tree)是n(n≥0)个结点的有限集。在任意一棵非空树中:
(1)有且仅有一个特定的被称为根(Root)的结点;
(2)当n>1时,其余结点可分为m(m>0)个互不相交的有限集T1,T2,…,Tm,其中每一个集合本身又是一棵树,并且称为根的子树(SubTree)。
结点的度(Degree):结点拥有的子树数称为结点的度(Degree)。度为0的结点称为叶子(Leaf)或终端结点。度不为0的结点称为非终端结点或分支结点。树的度:是树内各结点的度的最大值。
孩子和双亲:结点的子树的根称为该结点的孩子(Child),相应地,该结点称为孩子的双亲(Parent)。
结点的层次(Level):是从根结点开始计算起,根为第一层,根的孩子为第二层,依次类推。树中结点的最大层次称为树的深度(Depth)或高度。
如果将树中结点的各子树看成从左至右是有次序的(即不能互换),则称该树为有序树,否则称为无序树。
二,二叉树
二叉树(Binary Tree)的特点是每个结点至多具有两棵子树(即在二叉树中不存在度大于2的结点),并且子树之间有左右之分。
二叉树的性质:
(1)、在二叉树的第i层上至多有2i-1个结点(i≥1)。
(2)、深度为k的二叉树至多有2k-1个结点(k≥1)。
(3)、对任何一棵二叉树,如果其终端结点数为n0,度为2的结点数为n2,则n0=n2+1。
有很多关于树的术语,在这里不做过多的文字解释,不想画图了。下面我找了图来说明,图参考来自http://blog.csdn.net/u012152619/article/details/42059325,通过它可以直观地理解树的路径、根、父节点、子节点、叶节点、子树、层等概念
三,二叉查找树(左<中<右)
我们从一种特殊的、使用很广泛的二叉树入手:二叉查找树。
二叉查找树的性质:
(1)、若它的左子树不为空,则左子树上所有结点的值均小于它的根结点的值;
(2)、若它的右子树不为空,则右子树上所有结点的值均大于它的根结点的值;
(3)、它的左、右子树也分别为二叉查找树。
用一句话概括,二叉查找树的特点是,一个节点的左子节点的关键字值小于这个节点,右子节点的关键字值大于或等于这个父节点。
二叉查找树的基本操作是查找,插入,删除,遍历,下面一一介绍:
1,查找(search)
我们已经知道,二叉搜索树的特点是左子节点小于父节点,右子节点大于或等于父节点。查找某个节点时,先从根节点入手,如果该元素值小于根节点,则转向左子节点,否则转向右子节点,以此类推,直到找到该节点,或者到最后一个叶子节点依然没有找到,则证明树中没有该节点
代码是:
/** 查找元素,返回true */
public boolean search(E e) {
TreeNode<E> current = root; // 从根元素开始
while (current != null) {
if (e.compareTo(current.element) < 0) {//如果比当前元素值小,就指向当前元素的左子树
current = current.left;
}
else if (e.compareTo(current.element) > 0) {//如果比当前元素值大,就指向当前元素的右子树
current = current.right;
}
else // element等于 current.element
return true; //发现元素,返回true
}
return false;
}
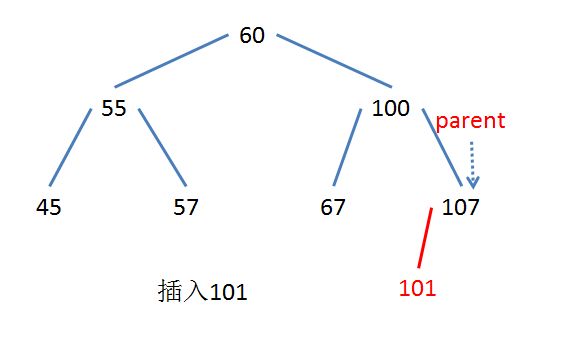
2,插入(insert)
插入一个新节点首先要确定插入的位置,关键思路是确定新节点父节点所在的位置。
代码:
/** 插入元素,成功返回true */
public boolean insert(E e) {
if (root == null)
root = createNewNode(e); // 如果是树空则创造一个跟节点
else {
// 标记当前父节点位置
TreeNode<E> parent = null;
TreeNode<E> current = root;
while (current != null)
if (e.compareTo(current.element) < 0) {
parent = current;
current = current.left;
}
else if (e.compareTo(current.element) > 0) {
parent = current;
current = current.right;
}
else
return false; // 有重复节点,不能被插入
// 创建一个新节点挂在父节点下
if (e.compareTo(parent.element) < 0)
parent.left = createNewNode(e);
else
parent.right = createNewNode(e);
}
size++;
return true; // 插入成功
}
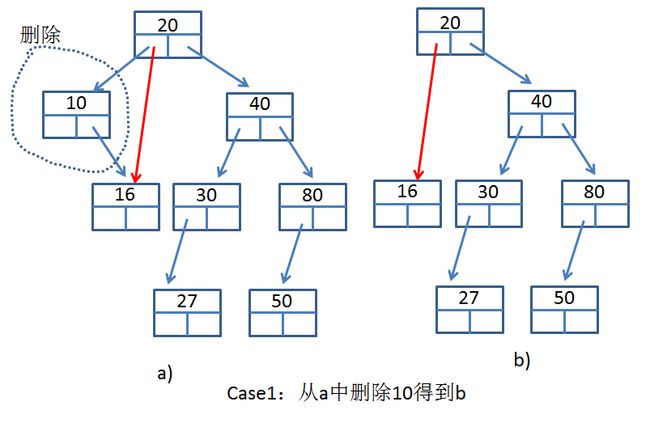
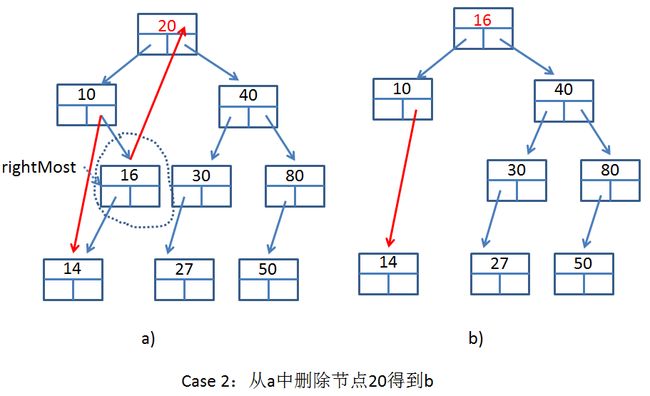
删除BST中的一个节点是最麻烦的操作,总结一下大概下面两种方法:
Case 1:删除点没有左孩子,这是只需要将该节点的父节点和当前节点的有孩子相连即可
Case2:删除点有左孩子.这种情况下先找到当前节点的左子树的最右节点,因为一个节点的左子树的最右节点也比右子树的最左节点小,把最右节点复制给删除点,然后删除最右节点
代码:
/** 删除节点,删除成功返回true,不在树中返回false*/
public boolean delete(E e) {
// 标记被删除的节点和该节点的父节点位置
TreeNode<E> parent = null;
TreeNode<E> current = root;
while (current != null) {
if (e.compareTo(current.element) < 0) {
parent = current;
current = current.left;
}
else if (e.compareTo(current.element) > 0) {
parent = current;
current = current.right;
}
else
break; // 元素在这个树中
}
if (current == null)
return false; // 元素不在树中
if (current.left == null) { // 第一种情况:元素没有左子树,把当前节点的右子树直接挂在其父节点的右子树上
// 把当前节点的右子树直接挂在其父节点的右子树上
if (parent == null) {
root = current.right;
}
else {
if (e.compareTo(parent.element) < 0)
parent.left = current.right;
else
parent.right = current.right;
}
}
else { // 第二种情况:元素有左子树,先找到当前节点的左子树的最右节点
//标记当前节点的左子树的父节点和最右节点
TreeNode<E> parentOfRightMost = current;
TreeNode<E> rightMost = current.left;
//一直向右,找到最右端的节点,因为一个节点的左子树的最右节点也比右子树的最左节点小
while (rightMost.right != null) {
parentOfRightMost = rightMost;
rightMost = rightMost.right; // 一直向右
}
/*
* 以上代码的目的是要找到删除节点的左子树最右节点 ,因为一个节点的左子树的最右节点也比右子树的最左节点小*/
// 找到最右节点后,放到当前要删除的位置
current.element = rightMost.element;
// 消除最右节点
if (parentOfRightMost.right == rightMost)
parentOfRightMost.right = rightMost.left;//把最右节点的左子树挂在其父节点的右子树上
else
// 具体情况: parentOfRightMost == current
parentOfRightMost.left = rightMost.left;
}
size--;
return true; // 删除成功
}
下面介绍一下二叉树的构成:
Tree.java
package com.hust.cn;
public interface Tree<E extends Comparable<E>> {
//查找元素
public boolean search(E e);
//插入元素
public boolean insert(E e);
//删除元素
public boolean delete(E e);
//中序遍历
public void inorder();
//后序遍历
public void postorder();
//前序遍历
public void preorder();
//返回大小
public int getSize();
//判空
public boolean isEmpty();
//返回树的迭代器
public java.util.Iterator iterator();
}
AbstractTree.java
package com.hust.cn;
public abstract class AbstractTree<E extends Comparable<E>>
implements Tree<E> {
//中序遍历
public void inorder() {
}
//后序遍历
public void postorder() {
}
//前序遍历
public void preorder() {
}
//判空
public boolean isEmpty() {
return getSize() == 0;
}
//返回树的迭代器
public java.util.Iterator iterator() {
return null;
}
}
BinaryTree.java
package com.hust.cn;
public class BinaryTree<E extends Comparable<E>>
extends AbstractTree<E> {
protected TreeNode<E> root;//节点类,是内部类
protected int size = 0;
/** 构造函数 */
public BinaryTree() {
}
/** 对象数组创建一个二叉查找树 */
public BinaryTree(E[] objects) {
for (int i = 0; i < objects.length; i++)
insert(objects[i]);
}
/** 查找元素,返回true */
public boolean search(E e) {
TreeNode<E> current = root; // 从根元素开始
while (current != null) {
if (e.compareTo(current.element) < 0) {//如果比当前元素值小,就指向当前元素的左子树
current = current.left;
}
else if (e.compareTo(current.element) > 0) {//如果比当前元素值大,就指向当前元素的右子树
current = current.right;
}
else // element等于 current.element
return true; //发现元素,返回true
}
return false;
}
/** 插入元素,成功返回true */
public boolean insert(E e) {
if (root == null)
root = createNewNode(e); // 如果是树空则创造一个跟节点
else {
// 标记当前父节点位置
TreeNode<E> parent = null;
TreeNode<E> current = root;
while (current != null)
if (e.compareTo(current.element) < 0) {
parent = current;
current = current.left;
}
else if (e.compareTo(current.element) > 0) {
parent = current;
current = current.right;
}
else
return false; // 有重复节点,不能被插入
// 创建一个新节点挂在父节点下
if (e.compareTo(parent.element) < 0)
parent.left = createNewNode(e);
else
parent.right = createNewNode(e);
}
size++;
return true; // 插入成功
}
/*创建一个新节点*/
protected TreeNode<E> createNewNode(E e) {
return new TreeNode<E>(e);
}
/** 中序遍历*/
public void inorder() {
inorder(root);
}
/** 从根节点中序遍历 ,递归方法*/
protected void inorder(TreeNode<E> root) {
if (root == null) return;
inorder(root.left);
System.out.print(root.element + " ");
inorder(root.right);
}
/**后序遍历 */
public void postorder() {
postorder(root);
}
/**从根节点后序遍历,递归方法 */
protected void postorder(TreeNode<E> root) {
if (root == null) return;
postorder(root.left);
postorder(root.right);
System.out.print(root.element + " ");
}
/**前序遍历 */
public void preorder() {
preorder(root);
}
/** 从根节点前序遍历,递归方法 */
protected void preorder(TreeNode<E> root) {
if (root == null) return;
System.out.print(root.element + " ");
preorder(root.left);
preorder(root.right);
}
/** 返回树的大小 */
public int getSize() {
return size;
}
/** 返回根节点 */
public TreeNode getRoot() {
return root;
}
/** 返回从根节点到一个具体元素的路径 */
public java.util.ArrayList<TreeNode<E>> path(E e) {
java.util.ArrayList<TreeNode<E>> list =
new java.util.ArrayList<TreeNode<E>>();//用数组存放路径上的元素
TreeNode<E> current = root; // 从根节点开始
while (current != null) {
list.add(current); // 添加当前元素到数组里
if (e.compareTo(current.element) < 0) {
current = current.left;
}
else if (e.compareTo(current.element) > 0) {
current = current.right;
}
else
break;
}
return list; // 返回节点数组
}
/** 删除节点,删除成功返回true,不在树中返回false*/
public boolean delete(E e) {
// 标记被删除的节点和该节点的父节点位置
TreeNode<E> parent = null;
TreeNode<E> current = root;
while (current != null) {
if (e.compareTo(current.element) < 0) {
parent = current;
current = current.left;
}
else if (e.compareTo(current.element) > 0) {
parent = current;
current = current.right;
}
else
break; // 元素在这个树中
}
if (current == null)
return false; // 元素不在树中
if (current.left == null) { // 第一种情况:元素没有左子树,把当前节点的右子树直接挂在其父节点的右子树上
// 把当前节点的右子树直接挂在其父节点的右子树上
if (parent == null) {
root = current.right;
}
else {
if (e.compareTo(parent.element) < 0)
parent.left = current.right;
else
parent.right = current.right;
}
}
else { // 第二种情况:元素有左子树,先找到当前节点的左子树的最右节点
//标记当前节点的左子树的父节点和最右节点
TreeNode<E> parentOfRightMost = current;
TreeNode<E> rightMost = current.left;
//一直向右,找到最右端的节点,因为一个节点的左子树的最右节点也比右子树的最左节点小
while (rightMost.right != null) {
parentOfRightMost = rightMost;
rightMost = rightMost.right; // 一直向右
}
/*
* 以上代码的目的是要找到删除节点的左子树最右节点 ,因为一个节点的左子树的最右节点也比右子树的最左节点小*/
// 找到最右节点后,放到当前要删除的位置
current.element = rightMost.element;
// 消除最右节点
if (parentOfRightMost.right == rightMost)
parentOfRightMost.right = rightMost.left;//把最右节点的左子树挂在其父节点的右子树上
else
// 具体情况: parentOfRightMost == current
parentOfRightMost.left = rightMost.left;
}
size--;
return true; // 删除成功
}
/** 获得中序迭代器 */
public java.util.Iterator iterator() {
return inorderIterator();
}
/** 创建一个迭代器类*/
public java.util.Iterator inorderIterator() {
return new InorderIterator();
}
// 中序迭代器类,内部类
class InorderIterator implements java.util.Iterator {
// 存储元素的数组
private java.util.ArrayList<E> list =
new java.util.ArrayList<E>();
private int current = 0; //数组中当前元素的位置
public InorderIterator() {
inorder(); // 中序遍历二叉树
}
/** 从根部中序遍历*/
private void inorder() {
inorder(root);
}
/** 中序遍历子树 */
private void inorder(TreeNode<E> root) {
if (root == null)return;
inorder(root.left);
list.add(root.element);
inorder(root.right);
}
/** 遍历下一个元素*/
public boolean hasNext() {
if (current < list.size())
return true;
return false;
}
/** 获得当前元素,并把指针指向另一个元素 */
public Object next() {
return list.get(current++);
}
/** 移出当前元素 */
public void remove() {
delete(list.get(current)); //删除当前元素
list.clear(); //清理数组
inorder(); //重新中序遍历数组
}
}
/** 清楚树的所有元素 */
public void clear() {
root = null;
size = 0;
}
/** 内部类,树的节点类 */
public static class TreeNode<E extends Comparable<E>> {
E element;
TreeNode<E> left;
TreeNode<E> right;
public TreeNode(E e) {
element = e;
}
}
}
TestBinaryTree.java
package com.hust.cn;
public class TestBinaryTree {
public static void main(String[] args) {
// 创建一个二叉查找树
BinaryTree<String> tree = new BinaryTree<String>();
tree.insert("George");
tree.insert("Michael");
tree.insert("Tom");
tree.insert("Adam");
tree.insert("Jones");
tree.insert("Peter");
tree.insert("Daniel");
// 遍历树
System.out.println("Inorder (sorted): ");
tree.inorder();
System.out.println("\nPostorder: ");
tree.postorder();
System.out.println("\nPreorder: ");
tree.preorder();
System.out.println("\nThe number of nodes is " + tree.getSize());
// 查找一个元素
System.out.println("\nIs Peter in the tree? " +
tree.search("Peter"));
// 从root到peter的一条路径
System.out.println("\nA path from the root to Peter is: ");
java.util.ArrayList<BinaryTree.TreeNode<String>> path
= tree.path("Peter");
for (int i = 0; path != null && i < path.size(); i++)
System.out.print(path.get(i).element + " ");
//利用数组构建一个二叉查找树,并中序遍历
Integer[] numbers = {2, 4, 3, 1, 8, 5, 6, 7};
BinaryTree<Integer> intTree = new BinaryTree<Integer>(numbers);
System.out.println("\nInorder (sorted): ");
intTree.inorder();
}
}
测试结果: