转载BP算法介绍好文
本文转载自《Belief Propagation 解决计算机视觉问题》,作者lansatiankong
Belief Propagtion在计算机视觉视觉中有相当广泛的应用,当然这一切离不开MRF、CRF等图模型的使用。
很多视觉问题可以表述成一个能量函数的形式,例如,图像的语义分割或者叫做image parsing问题可以表述成:
我们的目标是求这个函数的最小值,其中 P 是图像的像素集合, L 是图像的像素所属的标签集合,这些标签对应着我们要求的像素的某些量值,例如图像恢复问题中的原本的像素值,或是更高级的图像语义分割中像素所属于的类别。一个标注labeling f 所做的就是给图像的每个像素一个标签,可以把 f 看成一个向量或是矩阵,对应分配给图像的每个像素 p∈P 一个标签 fp∈L 然后我们用一个能量函数衡量这个标注的好坏。大部分能量函数都是由两个部分组成,第一个一般叫unary potential,叫一元势函数,第二项一般叫pairwise potential,点对势函数。一般一元势函数的作用是体现单个像素点似然标签,属于某个标签的概率高,那么这个值越小,也有叫label cost,将标签赋予该像素的损失,例如在图像恢复里面,像素有很大的可能性是没有被noise更改的,这样可以设原本像素的unary potential小一些;或者根据在图像语义分割里面每个像素求到的类条件概率 Dp(fp)=1−P(fp|p) ,似然越高,label cost当然越小。pairwise potential一般是衡量像素与像素之间的标签关系的,例如MRF,只会考虑位置相邻的像素的标签关系,关于相邻标签关系,一方面由于图像连续性,我们希望图像的相邻像素(特别是颜色纹理等特征相似的相邻像素)会有相同的标签,另一方面,我们也希望在一些必要的地方,例如物体的边缘什么的位置,能够保持这种边缘关系,能够有不同的标签,不要都over smooth成一个标签了,一般这个叫做discontinuity preserving property。 N 一般在CV里面一般就是图像的像素构成四连接grid graph的边。在【1】中解释到, Dp(fp) 是将标签 fp 分配给 p 的cost, W(fp,fq) 是分配两个相邻像素的标签为 fp,fq 的cost,也叫不连续cost,最小化这个函数和最大化MRF的后验概率是等价的。
接着上面的讨论,一般来说discontinuity cost是和相邻像素的差值有关系的,所以一般可以这样定义 W(fp,fq)=V(fp−fq) ,这样的话求的能量函数就成了
要解决这个问题可以用前一篇提到的belief propagation.也就是message passing
简单就是说对于每个像素都有一个属于某个类的belief,每个像素是四连接的,可以通过连接的边把这个belief传递出去,直到收敛,传播过程趋于稳定。
类似于上一篇,首先定义一个传递的消息, mtpq 就表示在第 t 次迭代中,从节点 p 传递给 q 的消息, m0pq 可以初始化成0。很明显,这个 mtpq 是一个 |L| 维的向量,|L|是标签的个数。
第一步,首先要计算Message
然后计算每个node属于不同label的belief
就是本身的label cost加上周围所有节点的message。
剩下的就是根据计算得到的belief bq(fq) 得到每个点的label
整个过程下来的时间复杂度是 O(nk2T) , n 是像素的个数 k 是label的个数, T 是收敛的到迭代次数。每个message需要计算 O(k2) (本身是k维的,而且还有的min函数),一共有 n 的像素,这样的话每一轮就需要 O(k2)O(n) 次迭代。
然后作者就想着怎么对这个过程进行加速了,首先是计算Message update的复杂度可以用 min convolution 的方法从 O(k2) 降低到 O(k) ,而且,对于一些特殊的graph,例如grid,计算belief只需要一半的message update就可以,而且这样只需要计算特定位置的message,还可以减少存储message所需要的内存.还有就是可以用一种coarse-to-fine 的方式进行message更新,使得迭代次数也可以减少。
1.降低计算Message的复杂性
首先,可以讲Message的计算公式重新写成
这里, h(fp)=Dp(fp)+∑mt−1s→p(fp)
这样把含有 fq 的项拿了出来,这个形式和图像的卷积公式有点类似,不过这里两个函数之间是加号,而卷积是乘法,这里外面是求最小值,所以这个式子一般叫 min convolution ,但是这样如何能够做到 O(k) 的复杂度呢?主要是考虑CV里面pariwise label cost的特殊结构,具体可以先看下面几个例子:
首先是最简单的例子,Potts Model,
Potts Model的一般形式
由于pairwise label cost只有两种可能,这样的话我们就可以只用一次最小化函数,
到这里就很明显了,里面有一个 O(k) 的操作求 minfp(h(fp)) ,但是这个在每次求 fq 的message中是个定值,所以只需要算一次就好,用不着每次循环都计算,所以最终的复杂性仍然是 O(k) ,另外不同的节点之间cost不同其复杂度也是 O(k) 的。
第二种情况是线性模型的cost,假设pairwise cost是根据label不同有不同的值,
取 d 和 c|x| 之间的最小值,设定一个上届 d 主要是为了保证discontimuity preserving.
为了证明是如何保持复杂度 O(k) 的,先考虑一个简单的情况,label cost没有被截断的时候,
这个式子该怎么看呢,【2】的作者给了一个很好的思考角度。为了方便理解我们先看里面, c|fp−fq|+h(fp) ,这明显就是一个二维的锥形,斜率是c,不过是平移到了点 (fp,h(fp)) , mtp→q(fq) 就是在所有的这些k个平移了的锥形里面取在 fq 位置的下届,用一个图可以很好的表示
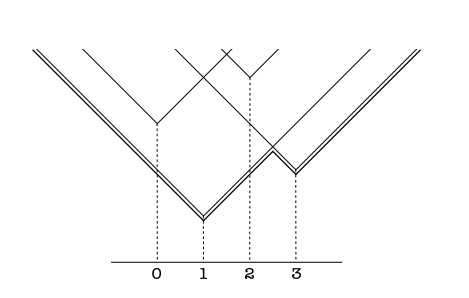
那么 mtp→q 这个向量就是从位置0到 k−1 所有锥形的下届组成的向量,可以用上图的最小面的粗线在0,1,2,3位置的值表示,但是这个值应该怎么用 O(k) 的算法求出来呢,因为我们仍然有k个锥形和k个位置要比较最小值。
这里用了两个循环,首先把 h(fq) 赋值给 mtp→q(fq) ,这是每个锥形的最小值,而且随之向两边伸展,每一个单位高度增加一个c,但是这个锥形的最小值并不是消息的值,消息的值有两个可能,一个是本身锥底位于该位置的锥底的值,另一个就是其它所有锥在该位置的值,
所以我们需要两层传播,第一次可以从做往右,把前面的锥在后面每个位置的最小值一次传递过去,我们只需记录该位置的最小值 m(fq) ,后面位置的最小值,要么是锥底在 fq+1 的锥底的值,要么和 m(fq) 在同一个锥上,值为 m(fq)+c ,
所以两次循环为
第二次循环把右边的信息更新到前面
在图上的例子里面,初始值是(3,1,4,6),c=1,第一次前向循环,(3,1,2,2),第二次后向循环,(2,1,2,2)
然后对于截断的Potts Model, m′(fq) 是两次循环得到的message
参考:
【1】http://wenku.baidu.com/view/0483de18a76e58fafab00384.html
【2】Efficient Belief propagation for Early Vision