三维图形变换与投影

                           三维图形变换与投影

一．目的：

       1．掌握三维图形的基本变换算法原理；

       2．掌握三维图形投影算法；

       3.  了解Open GL的基本用法。

二．要求：

      1．用Open GL在屏幕上绘制出空间三维坐标系。

      2.  用Open GL在屏幕上绘制出空间球，立方体和三角形。

      3.  用4次齐次坐标进行空间图形基本变换。

      4.  用透视投影规格化裁剪算法实现三维图形裁剪，并将裁剪结果在显示窗口显示出来。

三．原理和关键算法：

      1.  三维变换齐次坐标矩阵：

      

      2. 全比例变换：

     

     3.  缩放变换：

         变换矩阵主对角线上的元素a，e，j，s的作用是图形产生比例变幻。

      

      若a= e=j，则图形三方向的缩放比例相同；若a≠ e≠j，则图形产生畸变。

     4. 平移变换：

      

     5．旋转变换：

       1）绕X轴旋转θ角

   　   X坐标不变，Y，Z坐标发生变换。

         

      ２）绕Y轴旋转θ角

　　 Y坐标不变，X，Z坐标发生变换。

       

     ３）绕Y轴旋转θ角

　　 Z坐标不变，X，Y坐标发生变换。

     

  6. 三维裁剪：

  

   1）Sutherland-Cohen算法中的编码应为六位。括号中的条件适用于透视的情况，平行投影时用括号外的条件。

      点在视域上面，第一位为1，y>1, (y>z)

      点在视域下面，第二位为1，y<0, (y<-z)

      点在视域右面，第三位为1，x>1, (x>z)

      点在视域左面，第四位为1，x<0, (x<-z)

      点在视域后面，第五位为1，z>1, (z>1)

      点在视域前面，第六位为1，z<0, (z<zmin)

   设线段的起点和终点分别为P0(x0,y0,z0)和P1(x1,y1,z1)，直线方程可表示成参数形式

       x = x0 + (x1-x0)t,  

       y= y0 + (x1-x0)t, 

       x= x0 + (x1-x0)t     (4.39)

    和视域的边界面，例如y=1求交时，可由

      1=(y1 - y0)t’ + y0,       t’=(1-y0)/(y1-y0)

    求得交点的参数t’，再把t’代入（4.39），即可得交点的坐标。求P0P1和平面x=z的交点时，可把（4.39）代入x=z中求得交点处的参数

      –       t’=(z0-x0)/[(x1-x0)-(z1-z0)]   (4.40)

     把t’代入式(4.39)即可得到交点的坐标。

    2）三维图形的显示流程图

     采用二维裁剪的三维图形显示流程图

    

     在投影之前裁剪的理由：

     三维物体的表面通常被离散表示成多边形或折线，而对这类简单图元，三维裁剪同样比较简单。

     三维图形在显示过程中需要被消隐，做这个工作要有图形的深度信息，所以必须在投影之前完成 。 消隐很费时，如果在此之前裁剪（或部分裁剪）掉不可见的图形，可使需要消隐的图形减至最小。

四．关键代码：

     1.  平移变换：

void CDrawScene::translate3dMatrix(float Tx, float Ty, float Tz)
{
	CCgWuPing3dTransDoc *pDoc = (CCgWuPing3dTransDoc *)m_pView->GetDocument();	    
          whoObj_p->transMatrix[3][0] = whoObj_p->transMatrix[3][0] + Tx;
          whoObj_p->transMatrix[3][1] = whoObj_p->transMatrix[3][1] + Ty;
	  whoObj_p->transMatrix[3][2] = whoObj_p->transMatrix[3][2] + Tz;
}

     2.  绕X轴旋转：

void CDrawScene::rotateX3Dmatrix(float S, float C)
{
        CCgWuPing3dTransDoc*pDoc=(CCgWuPing3dTransDoc*)m_pView->GetDocument()；
	for (int i = 0; i < 4; i++) {
		float temp;
        temp = whoObj_p->transMatrix[i][1]*C - whoObj_p->transMatrix[i][2]*S;
               whoObj_p->transMatrix[i][2]=whoObj_p->transMatrix[i][1]*S+
               whoObj_p->transMatrix[i][2]*C;
	       whoObj_p->transMatrix[i][1] = temp;
	}
}

    3. 绕Y轴旋转：

void CDrawScene::rotateY3Dmatrix(float S, float C)
{
	CCgWuPing3dTransDoc *pDoc = (CCgWuPing3dTransDoc *)m_pView->GetDocument();
	for (int i = 0; i < 4; i++) {
	   float temp;
           temp = whoObj_p->transMatrix[i][0]*C + whoObj_p->transMatrix[i][2]*S;
	          whoObj_p->transMatrix[i][2]=-whoObj_p->transMatrix[i][0]*S+
                  whoObj_p->transMatrix[i][2]*C;
		  whoObj_p->transMatrix[i][0] = temp;
	   }
}

     4. 绕Z轴旋转：

void CDrawScene::rotateZ3Dmatrix(float S, float C)
{
        CCgWuPing3dTransDoc*pDoc=(CCgWuPing3dTransDoc *)m_pView->GetDocument();
	for (int i = 0; i < 4; i++) {
                float temp;
                temp = whoObj_p->transMatrix[i][0]*C - whoObj_p->transMatrix[i][1]*S;
	        whoObj_p->transMatrix[i][1]=whoObj_p->transMatrix[i][0]*S+
                whoObj_p->transMatrix[i][1]*C;
		whoObj_p->transMatrix[i][0] = temp;
	   }
}

     5. 空间裁剪：

void CDrawScene::pClipSpaceObject()
{
	int  i,j,k,pv,spCross;
	int  inCount,outCount;
	Gpoint_t polyClip[10];
	float sx,sy,sz,px,py,pz;
	BOOL objectVisible,clip;
        CCgWuPing3dTransDoc *pDoc = (CCgWuPing3dTransDoc *)m_pView->GetDocument();	

	for (k = 0; k < whoObj_p->polyCount; k++) {
		if (whoObj_p->objectSpace[k].polyVisible) {
			inCount = whoObj_p->objectSpace[k].polyCount;
			for (i = 0; i < inCount; i++) {
				polyClip[i].x = whoObj_p->objectSpace[k].transObject[i].x;
				polyClip[i].y = whoObj_p->objectSpace[k].transObject[i].y;
				polyClip[i].z = whoObj_p->objectSpace[k].transObject[i].z; }
			clip = true; 
			for (i = 0; clip && i < 6; i++) {  // Clip Box 6 Pane Cube 
				outCount = 0;
				sx = polyClip[0].x;
				sy = polyClip[0].y;
				sz = polyClip[0].z;
				pv = pVisible(sx, sy, sz, i);
				if (pv) outPut(sx, sy, sz, &outCount, whoObj_p->objectSpace[k].clipObject);
				for (j = 1; j < inCount; j++) {
					px = polyClip[j].x;
					py = polyClip[j].y;
					pz = polyClip[j].z;
					spCross = pLineCrossPane(sx, sy, sz, px, py, pz, i);
					if (spCross) pLineInterSectPane(sx, sy, sz, px, py, pz, i, 
						                            &outCount,whoObj_p->objectSpace[k].clipObject);
					sx = px;
					sy = py;
					sz = pz;
					pv = pVisible(sx, sy, sz, i);
					if (pv) outPut(sx, sy, sz, &outCount, whoObj_p->objectSpace[k].clipObject);
				}
				inCount = outCount;
				if (outCount == 0) clip = false;
				for (j = 0; clip && j < outCount; j++) {
					polyClip[j].x = whoObj_p->objectSpace[k].clipObject[j].x;
					polyClip[j].y = whoObj_p->objectSpace[k].clipObject[j].y;
					polyClip[j].z = whoObj_p->objectSpace[k].clipObject[j].z; }
				if (polyClip[0].x != polyClip[outCount-1].x &&
					polyClip[0].x != polyClip[outCount-1].y &&
					polyClip[0].x != polyClip[outCount-1].z) {
						polyClip[outCount].x = polyClip[0].x;
						polyClip[outCount].y = polyClip[0].y;
						polyClip[outCount].z = polyClip[0].z;
						inCount++;
				}
			}
			if (outCount != 0) objectVisible = true;
			whoObj_p->objectSpace[k].clipCount = outCount;
		}
	}
	whoObj_p->objectVisible = objectVisible;
}

     其中有些函数与二维下的多边形裁剪类似，这里不再一一列出。请查看二维下的多边形裁剪。

五．结果：

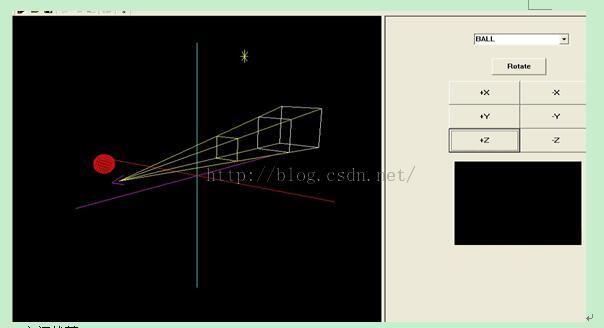
     1. 平移旋转变换：

     

    

    2. 空间裁剪：

    

    

   

六．实验总结：

    1. 运用Open GL实现三维图形的变换和裁剪。

    2. 充分利用二维与三维在图像处理的相似性，在图形裁剪时，先将三维图形透视投影到三个坐标平面，在用二维方法进行裁剪可以减少图形裁剪时的计算量。