机器学习系列(8)_读《Nature》论文,看AlphaGo养成
作者:龙心尘 && 寒小阳
时间:2016年3月。
出处:http://blog.csdn.net/longxinchen_ml/article/details/50900070
http://blog.csdn.net/han_xiaoyang/article/details/50903562
声明:版权所有,转载请联系作者并注明出处
1.文章声明
- 博主是围棋小白,下棋规则都记不清楚,也没有设计过棋类AI程序。这篇文章主要是阅读《Nature》论文及关于AlphaGo的相关文章的学习心得。
- 本文的主要目的是增进分享,交流学习,方便初学者了解AlphaGo中的算法,以及一些机器学习中的常见思路。真正的工程实现过程远比本文介绍得复杂。
- 本文更多是启发式地进行阐述与分析,包括一些作者结合自己的理解进行的简化处理。
- 文章中不严谨和理解不当之处,欢迎大家批评指出,我们努力修改完善。
2.围棋的业务特点
机器学习的第一步都是先了解业务。围棋的业务特点包括其基本规则、对弈特性和下棋的典型思路。根据这些业务特点,我们可以分阶段实现我们的围棋算法。
2.1 围棋的基本规则
- 使用方形格状棋盘及黑白二色圆形棋子进行对弈,
- 棋盘上有纵横各19条直线将棋盘分成361个交叉点,棋子走在交叉点上,
- 双方交替行棋,落子后不能移动,
- 以围地多者为胜。
- 并且双方可以相互吃子(提子),只要我方棋子将对方某一片紧邻的棋子周围围住,就可以将对方这片棋子吃掉。
2.2 对弈特性
基于以上规则,围棋对弈过程中有以下特性:
不像象棋、军棋那样盘面上的棋子越走越少,而是越走越多。所以一局棋从开始到结束,用一张标记好走棋顺序的棋谱就能保存绝大部分下棋的信息,是一个时间序列。如下图就是《Nature》论文中的樊麾与AlphaGo对弈的一个棋谱:

对弈从开局到中局变化都很大,尤其是中局,往往是一着不慎,满盘皆输。用数学的描述叫做估值函数(得分函数)非常不平滑。
- 到收尾阶段,由于棋盘上总体的棋子是越来越多的,其变化就越来越少。可以看成是一个动态收敛的过程。
- 状态空间非常大,约为 2×10170 ,超过目前的计算机的计算能力,无法通过暴力穷举解决。
2.3 下围棋的基本思路
而人类不需要搜索这么多状态空间也能够下好围棋,说明还是有规律的,只是这些规律比较抽象。我们机器学习算法就是要尽量找出人类下围棋的一些规律。我们可以简单总结一些人类下围棋典型思路如下:
- 首先是明确基本规则,这个方便。
- 其次是掌握一些基本“定式”,也就是在一个给定的局面下人类一般会怎么走,这个过程不涉及优劣的判断,也比较难以用确定性的规则描述。
- 基于对棋局未来演化情况的评估,决定当今当下的下棋策略。所谓“手下一着子,心想三步棋”。这是围棋最复杂的情况。
2.4 分阶段实现下棋算法
基于以上这些初步了解,我们可以分阶段实现我们的下棋算法:
- 第一步是学会人类下棋的一般定式,形成一些优秀考虑的下棋策略。
- 第二步是对落子之后的棋局演化做出有效评估,基于评估的结果优化自己的最终落子策略。
3. 先做一个baseline系统
现在我们思路大概有了,但仍然不知道模型的最终样子应该是怎样。此时我们建议先动简单手做一个baseline,然后在模型调优的过程中不断地分析问题、解决问题。这样就很有可能更快找到问题的最佳解决方案。设计baseline思路基本如下:
3.1 抽象成数学问题:多分类
通过以上分析可知,下围棋的过程就是一个不断地决策在哪个位置落子的过程。在落子之前,你已知棋盘上所有已落子的情况。而棋盘上总共就 19×19 =361个位置,所以落子就是一个361选1的多分类问题。将多分类问题转换成简单的2分类问题来处理,(采用one-to-rest的思路,)则需要361个2分类的分类器,每个分类器只评估落在361个位置中某1个具体位置的分数,再从这361个结果中中挑选分数最大的位置来落子。
3.2 哪些特征,如何选择?
分类器的输出我们知道了,就是361个标签。那分类器的输入又是哪些特征呢?其实就是当前的棋盘分布。
我们先考虑第一类特征。围棋一共是361个交叉点,每个交叉点有三种状态(白子、黑子、无子):可以用1表示黑子,-1表示白字,0表示无子。于是一个361维度的向量就可以完全表示当前棋盘的情况。理论上说,只输入这些特征就可以了。如下图就是演示用矩阵表示棋局状态的情况,而矩阵拉长就是一个向量了:

但是,因为围棋的极端复杂性,这些棋子(输入特征)的关系是非线性的。虽然理论上采用神经网络的算法可以处理非线性特征,但是计算量和对资源的消耗都太大。相反,如果有依据地增加一些新的特征的维度,使特征间的非线性关系不那么复杂,将使得模型变得更加简单、更加便于训练,优势还是很明显的。
那怎么增加更多的特征呢?这就需要利用部分围棋领域中的知识,比如围棋中的术语:气、目、空等概念都可以作为我们构造新特征的基础。在AlphaGo的论文中就是采用了以下更多的特征:
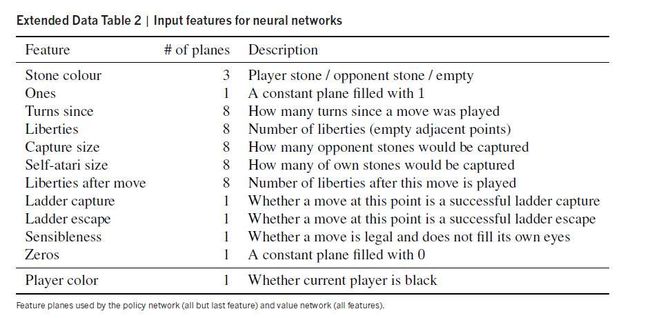
所以,输入模型的特征是一个361×n维度的向量。基于这些向量来训练模型。
最终,AlphaGo只依靠一个13层的卷积神经网络就能训练出一个比较好的落子分类器。比起图像识别竞赛用到的20、30层的深层神经网络还是比较浅了。这些都是特征工程的功劳。
3.3 初步采用什么样的模型?
我们了解到,下围棋的算法本质上就是一个分类器,而最简单的分类器就是逻辑回归。可以预期它的分类效果不一定很好,但是速度非常快,在需要快速迭代的业务场景中可能有优势。所以逻辑回归是我们考虑的一类模型。
但是在复杂的围棋博弈中,需要更多高维度的抽象特征,这些构造起来非常麻烦,而经过我们之前的博文介绍,神经网络具有这样抽象高维特征的能力。但是神经网络有许多种类,什么卷积神经网络、全连接神经网络、反馈神经网络等等,到底用哪一种呢?
我们可以继续研究围棋的业务特点来寻找启发。我们发现,围棋的棋盘本来就是个 19×19 的矩阵,真有点像一张 19×19 像素的照片。而处理图像照片的最典型神经网络就是卷积神经网络。而且我们之前的博文专门介绍过卷积神经网络,其最关键特质的在于假设图像空间中局部的像素联系较为紧密,所以其卷积层的每个神经元只关注上一层的一些局部区域,这样能够充分利用输入数据的二维结构和局部特性,减少运算过程中的参数。你可以想象成,上一层的数据区,有一个滑动的窗口,只有这个窗口内的数据会和下一层的某个神经元有关联。而这种 “局部连接性”刚好与围棋的一些特点相似,比如围棋的大部分争夺是在局部区域进行的,不同的局部争夺共同组成了围棋的全局性。所以卷积神经网络也是我们考虑的一类模型。
3.4 采用哪些数据做训练?
标签、特征、模型基本定好了,剩下的就是数据了。从哪里得到数据呢?还是回到我们之前的棋谱,那本质上是个有时间顺序的序列。如果我们能够搜集到大量标记好落子顺序的棋谱,每一步落子之前的局面全都作为特征(s,361×n维度的向量),这一步落子位置作为标签(a,361维度的向量),那不就得到了大量的有标注的数据< s , a >吗?
这还是得感谢网络时代,如今网络上有大量棋牌室,全都记录了人类下棋的过程,每天都产生大量有标注的数据。DeepMind就是直接从围棋对战平台KGS(可以理解成外国的联众围棋游戏大厅)获得16万局6至9段人类选手的围棋对弈棋谱,总共有3000万个的< s , a >位置,训练出来了一个类似人类下棋行为的模型。
4. 分析baseline的优化思路
DeepMind团队基于卷积神经网络和逻辑回归做了两个模型:一个叫做“监督学习策略网络” pσ (supervised learning (SL) policy network pσ ,田渊栋大神称作“走棋网络”),一个叫做“快速策略” pπ (fast policy pπ ,田渊栋大神称作“快速走子”**)。其实就是两个版本的落子选择器(分类器)。

4.1 评估baseline的效果
这个两个模型模型的效果如下:
- “监督学习策略网络”已经可以和业余水平的人类选手过招,能正确符合57%的人类落子行为,互有胜负。
- 可以把“快速策略”看做是“监督学习策略网络”的轻量级版本,它能够比“监督学习策略网络”快1000倍,但是只能正确符合24%的人类落子行为。
- 总体来说还是蛮惊人的。但是距离职业棋手,还是有很大的距离。
4.2 分析其下棋水平不高的原因
为什么baseline的下棋水平不高呢?猜测可能有以下几个原因:
- 我们主要是拿网络棋牌室的数据去训练,这些人的水平本来就离顶尖职业棋手就有相当大一段距离。俗话说:“跟臭棋篓子下棋,越下越臭”。与大量业余选手下棋,训练出来的行为也难以达到职业水准。
- 古往今来,真正顶尖的棋手本来就不多,顶尖的对局棋谱相应也就不多,拿这些数据做训练远远不够。
- 更本质的问题是,我们的“估值函数”有问题。无论是卷积神经网络还是逻辑回归,都可以近似理解为基于3000万个的有标注的数据< s , a >,评价在当前局面s下,落在某一位置a的概率,也就是p(a|s)。我们选择p(a|s)取最大值情况下的落子位置a。但这个过程没有考虑棋局的输赢信息!也就是说赢棋的落子方案也学,输棋的落子方案同样学习。这样的话,让模型怎么去分辨自己落子是赢棋还是输棋的落子方案呢?
- 即便分出了赢棋输棋方的落子方案,赢棋者的落子不一定都是好棋(如两个臭棋篓子下棋),输棋者的落子不一定都是差棋(如两个顶尖高手的精彩对弈)。那到底应该学习赢棋过程中的哪一步落子< s , a >呢?像baseline这样的模型看来更适合学习对弈双方都会走的棋路,也就是常见的“定式”。
- 更进一步,落子之后的棋局演化情况在上面的模型中根本没有体现。不把这样的行为考虑进来估计很难在棋力上有一个质的飞跃。
4.3 从对原因的分析中产生优化的思路
经过以上的原因分析,我们大致知道猜想到了问题的所在,由此可以进一步确定我们的优化思路:
- 核心目标是改进评估函数,使之更好地体现某一步落子对全局的输赢结果的影响,以全局的输赢为目标进行优化。
- 一方面,可以基于历史棋局的输赢情况进行重新训练。如果训练数据不够,可以考虑通过落子选择器自己与自己对局来增加训练样本数或者强化学习。
- 另一方面,在下棋实战的时候,需要对棋局的演化情况有一个评估,需要蒙特卡罗树搜索(Monte Carlo Tree Search,MCTS)。具体展开内容见后文。
- 将两个指标综合评估,得到落子优劣情况的评判。指导我们落子。
5. 基于历史棋局评估落子优劣:估值网络
5.1 采用新的标签
在之前的模型中,我们是基于标注数据< s , a >进行训练的,也就是以当前局面s作为特征,下一步落子a作为标签。现在我们要基于局面整体的输赢进行训练,就要对原有的标签和特征进行改造。
需要增加新的标签z,表示局面对应的胜负情况:可以用1表示赢棋,-1表示输棋,0表示和棋(博主理解是“多劫循环”,也就是双方可以无休止地走下去的情况)。
而特征就是(s,a),它表示在a处落子之后的新的局面(本质上还是一个局面,可以用s’表示,《Nature》原文就是这样表示的)。
也就是说基于有标注的数据<(s,a),z>(表示当前局面为s,下一步落子为a的新局面下,输赢情况为z的数据)进行训练。
5.2 采用更多的数据
既然要基于历史棋局,可不可以直接以之前的16万局棋谱的输赢情况和落子情况一起进行训练呢?DeepMind团队试了一试,发现结果过拟合。
分析原因,大概就是我们刚才说的赢棋者的落子不一定都是好棋(如两个臭棋篓子下棋),输棋者的落子不一定都是差棋(如两个顶尖高手的精彩对弈)的情况。围棋的落子是相互之间强烈相关(strongly correlated) 的,有时候一两着棋就觉得了整个棋局的输赢。那到底应该学习赢棋过程中的哪一两步落子< s , a >呢?
其实我们可以换一个思路。如果真存在一两着决定胜负的棋,那就说明其他的走法很可能就会演化到输棋,那把演化到输棋的棋局也拿过来进行训练,就可以在这一步棋上训练出赢棋的概率很高的权重。 而之前过拟合的原因很可能就是我们训练数据当做仍未穷尽棋局演化的各种可能,把臭棋也当做好棋来学了。所以需要想一个办法产生更多高质量的棋局演化可能用来训练。
既然靠人类对弈已经满足不了机器的胃口,那就用机器自己与自己对局来增加训练样本数,这就是传说中的左右互搏。比如开局,先用某个落子选择器走n步,由于n是随机的,这就产生出n个局面分支。觉得局面还不够多样化,再完全随机掷m次骰子,就又在每个局面分支上产生m新的局面分支。如此循环往复,就得到了非常丰富的局面s和这些局面对应的结果z。有了这些训练样本< s , z >,再加上卷积神经网络,就可以得到一个函数 v(s) ,输出在局面s下的赢棋概率。
按《Nature》原文的说法,他们通过自我博弈(self-play)产生了3000万个标注样本< s , z >,每个样本的局面s都来自不同的一局棋(each sampled from a separate game),以此来防止过拟合(这些挑出来的样本是否可能也是臭棋?)。注意,之前也是3000万个标注样本< s , z >,但它们只来自于16万局人类博弈的棋谱。
而基于此训练出来的函数叫做“估值网络”(value network vθ ),输入的是361×n维度的向量,输出的是一个值,也就是在该局面下胜利的概率。
5.3 估值网络与走棋网络下棋的对比
我们知道,走棋网络输入的s是361×n维度的向量,下一步落子位置a是361维度的向量。其下棋规则是判断选择p(a|s)取最大值情况下的落子位置a。p(a|s)就是模型的估值函数。
而估值网络输出的只是一个值 v(s) 。那判断下一步棋的落子位置呢?其实只要将下一步落子产生的新局面(s,a)作为输入s’,求出各个新局面的 v(s′) ,选择 v(s′) 取最大值情况下的落子位置a就行了。 v(s′) 就是模型的估值函数。
所以这两个网络作为落子选择器的差别本质上就是估值函数的算法不一样。
5.4 增强学习
我们继续分析,既然走棋网络p(a|s)可以自己产生数据,那么可否用自己产生的数据来训练走棋网络p(a|s)自己(而不是估值网络 v(s) )呢?而这就是增强学习的思想。

比如我们已经有了一个“走棋网络” pσ ,先用 pσ 和 pσ 对弈,比如1万局,就得到了一万个新棋谱,加入到训练集当中,训练出 pσ1 。然后再让 pσ1 和 pσ1 对局,得到另外一万个新棋谱,这样可以训练出 pσ2 ,如此往复,可以得到 pσn 。我们给 pσn 起一个新名字,叫做“增强学习的策略网络” pρ (reinforcement learning (RL) policy network pρ )。这时,再让 pρ 和 pσ 对局,在不用任何搜索的情况下赢棋的概率可达80%,效果拔群。
当然,具体的训练过程比较复杂。这里先不展开,仅对其具体效果进行分析。既然 pρ 这么强,我们在实战中直接用这个模型怎么样?可惜,这样的方法反而不如之前的“走棋网络” pσ 。《Nature》的论文中认为这可能是因为增强学习的策略网络是落子选择过于单一,基本就只选择它认为最好的那样走法(the single best move),而人类的棋手更愿意思考更多的有前途的路数(a diverse beam of promising moves)再决策。所以增强学习“还有很长的路要走”(田渊栋)。
但是增强学习可以提供更多质量更好的样本便于估值网络 v(s) 去训练。这样, v(s) 就可以给出下一步落子在棋盘上任意位置之后,如果双方都使用 pρ 来走棋,我方赢棋的概率。如果训练 v(s) 的时候全部都使用“走棋网络” pσ 而不用增强学习的策略网络 pρ 呢?实验表明基于 pρ 训练的 v(s) ,比基于 pσ 训练的 v(s) 的效果更好。
5.5 评估估值网络的效果
实践表明:估值网络 v(s) 对棋局输赢的预测效果要好于快速走子 pπ 结合蒙特卡罗树搜索接结果,也接近达到了走棋网络 pσ 结合蒙特卡罗树搜索接效果,而且其计算量是后者的1/15000(using 15,000 times
less computation)。
注意这里是对输赢的预测效果,而不是对落子可能性的预测。

6. 基于棋局演化评估落子优劣:蒙特卡罗树搜索
以上的方法我们都是基于当下的落子情况来评估落子路径优劣的。但人类的下棋思维是“手下一着子,心想三步棋”(selects actions by lookahead search),要对之后的棋局有个评估。那怎么让机器去思考接下来的发展呢?这就需要传说中的蒙特卡罗树搜索(MCTS)。
6.1 基于估值网络 v(s) 的MCTS
我们就先不说蒙特卡罗树搜索(MCTS)的术语吧,什么选择、扩展、模拟、反向传播啥的的。这里直接以下棋的思维方式来解释这个过程,尽量生(shuo)动(ren)些(hua)。
首先,我们有一个“走棋网络” pσ ,它生成了一个当前局面s的下一步走棋位置 a1 的概率分布。“走棋网络”的特点是模拟人类的常见走棋行为,但并不评估走棋之后的赢棋的概率(赢棋的概率与分布概率是两个不同的概念)。但可以假设,优秀的走棋路数应该在人类常见的走棋范围内,这就大大减少了需要考虑的可能性。那怎么从这些选择中找出最优的那个落子呢?咱不是刚好有个估值网络 v(s′) 吗?直接用它筛选赢棋的概率较高的可能落子局面 (s,a1) 不就可以了吗?
这已经完成了一步落子选择,但是距离“手下一着子,心想三步棋”的标准还差一些。那就继续假设走了 a1 之后,再考虑对方最可能怎么走。其思路与上面一样。那这样对方走了一招 a2 。紧接着可以再走一着 a3 。
好了,现在走了3步棋了。是不是就够了呢?未必。如果评估 v(s,a1) 的赢棋的概率是70%, v(s,a1,a2) 对方的赢棋的概率是60%(对应我方赢棋的概率是-60%),而走到第三步的时候评估的赢棋的概率 v(s,a1,a2,a3) 是35%呢?那你还要不要走 a1 这个位置?

这需要我们重新理解 v(s) 的实际意义:它用来预测该局面以增强学习的策略网络 pρ 的方式自我博弈后的赢棋的概率(predicts the winner of games played by the RL policy
network against itself)。而在我们蒙特卡罗树搜索过程中,不是用 pρ 的方式来选择落子的,所以不符合 v(s) 的定义。这就需要用新的方法来评估局面s下的赢棋的概率,也就是要对原来位置的赢棋的概率 v(s) 进行更新。那怎么更新呢?最简单的方法就是加权平均。为了不至于混淆,我们直接用 v∗ 来表示某一局面的赢棋的概率估值函数。刚开始时 v∗(s,a1)=70% ,而下完第三步后其更新为:
v∗(s,a1)=(70%−60%+35%)/3=15% 。
此时 v∗(s,a1) 已经变为15%,已经不是之前的70%,也就是说 a1 的位置可能不是赢棋的概率最大的位置了。需要重新挑选出一个位置 a′1 ,使得 v∗(s,a′1) 达到最大值,然后继续推演并不断更新不同位置的 v∗(s) 。(其实,在第2步对方落子的时候就应该更新 v∗(s,a1) 了,过程与上面类似。这里只是做了一个简化处理,便于理解。)
这就是蒙特卡罗树搜索的基本过程。可见,这套思路是可以不断演化下去的,越到后面,算出来的 v∗(s,a1) 应该越准确,当时间限制到的时候(围棋比赛有时限规则,因此时间规划也是一门学问),就可以返回出最佳位置 a1 了。
这种算法的一个好处是:可以并行化,因此可以大量提高计算速度。
它还有一个好处,就是:它演化出来的各种状态都可以保存起来,如果对方的落子就在自己的演化路径之中,这些状态就可以直接拿来用了。这就节省了大量运算时间。
需要说明的是,这里只是对蒙特卡罗树搜索做一个原理性的简化解释。真实的搜索过程可以增加许多策略,远比这里复杂。对MCTS感兴趣的读者可以看这篇文章。
6.2 基于快速走子 pπ 的MCTS
其实,我们还有另一种蒙特卡罗树搜索。基本演化过程与上面类似,但是选择落子的方式是基于快速走子 pπ 的。
首先,我们还是有一个“走棋网络” pσ ,还是由它先挑出一些人类常见的走棋可能。那我们对于各种可能状态直接用快速走子 pπ 一路走到底决出胜负。比如 pσ 提供三种落子可能,都用快速走子 pπ 模拟对局到底,得到的结果是2胜1负。以1表示胜,-1表示负。则“胜利”的落子选项的估值函数 v∗(s,a1) =1
然后,对手从“胜利”的落子选项中用“走棋网络” pσ 再拓展出3个落子可能,同样都用快速走子 pπ 模拟对局到底,得到的结果是2胜1负。
此时可以更新 v∗(s,a1)=(1+1−1)/3=1/3 ,我方再基于对方的落子局面用“走棋网络” pσ 再拓展出一些走棋可能,同样都可以继续用快速走子 pπ 模拟对局到底,得到结果后返回更新所通过的各个走子状态的的估值函数 v∗(s) 。如此不断反复。
这就体现出 pπ 的快速反应速度的优越性了。速度越快,模拟出来的未来对局就越多,对落子之后的局面判断就越准了。
6.3 综合两种搜索策略形成新的估值函数
这两种搜索各有优劣,而且在一定程度上互补。所以DeepMind将这两种策略组合到一起,效果就有质的飞跃了。以下是他们对比各种组合方式的结果:

其组合方式非常简单粗暴,就是做一个算术平均:
v∗=vθ+z2,(z就是快速走子后的返回的胜负结果)
工程实现上,还对估值函数增加了一个附加值(bonus)。目的是在快速定位比较好的落子方案的同时,又给其他小概率位置一定的探索可能,增加搜索丰富性。
其实蒙特卡罗树搜索是一个很传统的技术,但是如果不用先验的知识随机搜索,这棵树的宽度和深度要非常巨大才能返回一个相对靠谱点的值,这样的计算量是天文数字。但是通过16万局人类对弈训练出来的“走棋网络” pσ ,能够砍掉很多小概率的分支,减少搜索的宽度。而通过同样数据训练出来的“快速走子” pπ ,和通过3千万局机器对弈训练出来的“估值网络” v(s) ,能够共同使得在探索深度比较小的情况下,返回比较好的局面估值效果,减少了搜索的深度。再加上一些细节的策略,整体的效果就是减少了计算量,提高了预测精度。
7. 总结
到此为止,AlphaGo的算法原理基本介绍完了。其实也并不复杂,而且这些都不是AlphaGo或者DeepMind团队首创的。但是强大的DeepMind团队将这些结合在一起,再加上Google公司的超级计算资源,成就了超越绝大部分顶尖棋手的人工智能。真令人赞叹不已,向这些背后的工程师致敬。
8. 参考文献
《Nature》:Mastering the game of Go with deep neural networks and tree search
田渊栋:AlphaGo的分析
How AlphaGo Works
木遥:关于 AlphaGo 论文的阅读笔记
董飞编译How AlphaGo Works
袁行远:左右互搏,青出于蓝而胜于蓝?—阿尔法狗原理解析
Introduction to Monte Carlo Tree Search