hdu 1055 Color a Tree 贪心

Color a Tree

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 1096    Accepted Submission(s): 357

Problem Description

Bob is very interested in the data structure of a tree. A tree is a directed graph in which a special node is singled out, called the "root" of the tree, and there is a unique path from the root to each of the other nodes. 

Bob intends to color all the nodes of a tree with a pen. A tree has N nodes, these nodes are numbered 1, 2, ..., N. Suppose coloring a node takes 1 unit of time, and after finishing coloring one node, he is allowed to color another. Additionally, he is allowed to color a node only when its father node has been colored. Obviously, Bob is only allowed to color the root in the first try. 

Each node has a “coloring cost factor”, Ci. The coloring cost of each node depends both on Ci and the time at which Bob finishes the coloring of this node. At the beginning, the time is set to 0. If the finishing time of coloring node i is Fi, then the coloring cost of node i is Ci * Fi. 

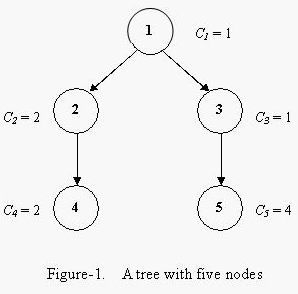
For example, a tree with five nodes is shown in Figure-1. The coloring cost factors of each node are 1, 2, 1, 2 and 4. Bob can color the tree in the order 1, 3, 5, 2, 4, with the minimum total coloring cost of 33.



Given a tree and the coloring cost factor of each node, please help Bob to find the minimum possible total coloring cost for coloring all the nodes.

 

Input

The input consists of several test cases. The first line of each case contains two integers N and R (1 <= N <= 1000, 1 <= R <= N), where N is the number of nodes in the tree and R is the node number of the root node. The second line contains N integers, the i-th of which is Ci (1 <= Ci <= 500), the coloring cost factor of node i. Each of the next N-1 lines contains two space-separated node numbers V1 and V2, which are the endpoints of an edge in the tree, denoting that V1 is the father node of V2. No edge will be listed twice, and all edges will be listed. 

A test case of N = 0 and R = 0 indicates the end of input, and should not be processed. 

 

Output

For each test case, output a line containing the minimum total coloring cost required for Bob to color all the nodes.

 

Sample Input

   
   
   
   

    
    
    
    5 1
1 2 1 2 4
1 2
1 3
2 4
3 5
0 0
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    33
   
   
   
   

题意：一棵树，父亲染色以后，这个节点才允许被染色。染色的代价= c[i]*t c[i] 表示这个点的权值，t表示这个点被染色的时间。

以为是dp，没想到是贪心。这个题出的太有意思了。

贪心策略： 选择一个点，如果这个点的权值最大，必然如果他的父亲被染色了，就一定会先染色这个点。

那么这个节点就和他的父亲被绑定在一起了。

绑定以后，他们的权值=c[i]+c[fa[i]]， 因为父亲先染色，孩子后染色，所以染父亲需要耗费  c[fa[i]]+2* c[i]的代价 因为是先后连续的关系

选择点的策略  有多个点绑定以后，他的节点数num[i]=与这个节点绑定的点的个数

选择 c[i]/num[i]最大的节点与他的父亲合并即可。

代码如下：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

#define maxn 1007
int total[maxn];
int c[maxn];
int fa[maxn];
int pre[maxn];
int num[maxn];
int find(int u){
    if(u == pre[u]) return u;
    return pre[u] = find(pre[u]);
}
int main(){
    int n,r;
    while(scanf("%d%d",&n,&r),n+r){
        for(int i = 1;i <= n; i++)
            scanf("%d",&c[i]);
        fa[r] = 0;
        int u,v;
        for(int i = 0;i < n-1;i++){
            scanf("%d%d",&u,&v);
            fa[v] = u;
        }
        for(int i = 0;i <= n; i++)
            pre[i] = i,num[i]=1;
        memset(total,0,sizeof(total));

        c[0] = 0;
        for(int i = 0;i < n; i++){
            u = 0;
            for(int j = 1;j <= n; j++){
                if(pre[j] == j){
                    if(u == 0 || c[u]*num[j]<c[j]*num[u]){
                        u = j;
                    }
                }
            }
            v = find(fa[u]);
            total[v] += num[v]*c[u]+total[u];
            num[v] += num[u];
            c[v] += c[u];
            pre[u] = v;
        }
        printf("%d\n",total[0]);
    }
    return 0;
}