<编程珠玑>笔记(二) 三个算法

 在第二章里，作者提出了三个问题，然后慢慢引出对应的算法实现。

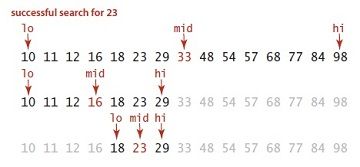
1  Binary search 二分查找

  Given a sequential file that contain at most 4x10⁹ 32-bit integers in random order, find a 32-bit integer that is not in the file.

  How would you solve this problem with ample main memory?

  How would you solve it if you could use several external "scratch" files but only a few hundred bytes of main memory? 

1)  bitmap technique

  With ample main memory, we could use the bitmap technique and dedicate 2³² 8-bit bytes to a bitmap representing the integers.

2)  binary search

          

  The insight is that we can probe a range by counting the elements above and below its midpoint: either the upper or the lower range has at most half the elements in the total range. Because the total range has a missing element, the smaller half must also have a missing element.

  Its only drawback is that the entire table must be known and sorted in advance.

 

2  Rotate -> reverse

  Rotate a one-dimensional vector x of n elements left by i positions. For instance, with n=8 and i=3, the vector abcdefgh is rotated into defghabc.

  Can you rotate the vector in time proportional to n using only a few dozen extra bytes of storage?

1) time and space constraints

  space-expensive -- copy the first i elementsto a temporary array, move the remaining (n-i) elements left i places, and then copy the first i from the temporary array back to the last position in x.

  time-expensive -- define a function to rotate x left one position(in time proportional to n) and call it i times.

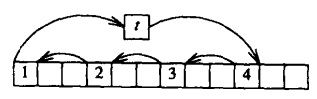
2) delicate juggling act

  move x[0] to the temporary t, then move x[i] to x[0], x[2i] to x[i], and so on, until we come back to taking an element from x[0], at which point we instead take the element from t and stop the process.

  When i is 3 and n is 12, that phase moves the elements in this order. If that process did not move all the elements, then we start over at x[1], and continue until we move all the elements.

 

3) revese

  starting with ab, we reverse a to get a^rb, reverse b to get a^rb^r, and then reverse the whole thing to get (a^rb^r)^r, which is exactly ba

reverse(0, i-1)    // cbadefgh
reverse(i, n-1)    // cbahgfed
reverse(0, n-1)    // defghabc

 

3  Signatures

  Given a dictionary of English words, find all sets of anagram.

  For instance, "pots", "stop" and "tops" are all anagrams of each other.