BZOJ 1502 NOI2005 月下柠檬树 Simpson自适应公式
题目大意:给定一棵由圆台和圆锥构成的柠檬树,月光以α的夹角平行射向地面,求阴影部分面积
补充题目大意:看到这题我产生了心理阴影,求阴影部分面积
题目不好分析,但其实就是求一堆圆和一堆梯形的面积交
样例如图(画的有点烂),将顶点看做半径为0的圆,则图中圆的半径即为给定圆的半径,圆心距为h/tan(α),直线为两圆公切线
这题我们采用辛普森自适应公式
首先辛普森公式见度受百科 http://baike.baidu.com/view/2710883.htm?fr=aladdin
比较遗憾的是 辛普森公式虽然强大 但是只能处理三次以内的函数,对于无理函数完全无力,所以没有办法求圆的精确面积
但是我们可以做一些处理,让这个公式“万能”起来
首先我们对于任意函数f(x),取f(l),f(r)以及f(mid)强行套用辛普森公式,这相当于求了一个过( l,f(l) ), ( r,f(r) ), ( mid,f(mid) )三点的抛物线的面积
但是这样得到的面积只能是粗略面积
于是我们进行一步递归处理
对于l~r部分求出的面积,我们利用辛普森公式求出l~mid和mid~r两部分的面积,然后我们把l~r部分的面积与分部求出的两部面积之和进行比较,若在误差允许范围之内则返回l~r部分的面积,否则递归处理l~mid和mid~r
即
double Get_Area(l,r)
{
double mid=(l+r)/2.0;
if( Simpson(l,mid) + Simpson(mid,r) - Simpson(l,r) < eps )
return Simpson(l,r);
return Get_Area(l,mid) + Get_Area(mid,r);
}
然后就过去了
此外,公切线的求法物理老师讲过,但是被我略过了,现在想想我真是对不起任何一科老师了、、、
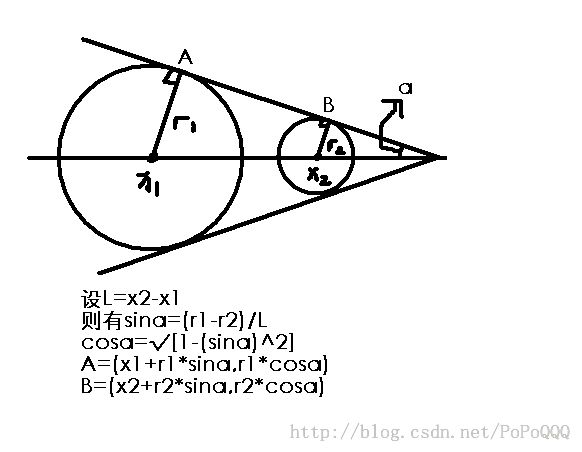
废话不说上图
这个公式在r1<r2时同样适用 所以不要加绝对值
注意两圆内含时不存在公切线
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define eps (1e-6)
#define M 510
using namespace std;
struct point{ double x,y; };
struct line{
point p1,p2;
double k,b;
line(){}
line(double x1,double y1,double x2,double y2)
{
p1.x=x1;
p1.y=y1;
p2.x=x2;
p2.y=y2;
}
void Get_Function()
{
k=(p1.y-p2.y)/(p1.x-p2.x);
b=p1.y-k*p1.x;
}
double f(double x)
{
return k*x+b;
}
}lines[M];
struct Circle{ double x,r; }circles[M];
int n,tot;
double alpha;
double f(double x)
{
int i;
double re=0;
for(i=1;i<=n;i++)
{
double dis=fabs(x-circles[i].x);
if( dis - circles[i].r > -eps )
continue;
double y = sqrt( circles[i].r * circles[i].r - dis * dis );
re=max(re,y);
}
for(i=1;i<=tot;i++)
if( x>=lines[i].p1.x && x<=lines[i].p2.x )
re=max(re, lines[i].f(x) );
return re;
}
double Simpson(double fl,double fr,double fmid,double h)
{
return h*(fl+4*fmid+fr)/6.0;
}
double Get_Area(double l,double r,double mid,double fl,double fr,double fmid,double area)
{
double lmid=(l+mid)/2.0;
double rmid=(r+mid)/2.0;
double flmid=f(lmid);
double frmid=f(rmid);
double larea=Simpson(fl,fmid,flmid,mid-l);
double rarea=Simpson(fmid,fr,frmid,r-mid);
if( fabs(larea+rarea-area) < eps )
return area;
else
return Get_Area(l,mid,lmid,fl,fmid,flmid,larea)+
Get_Area(mid,r,rmid,fmid,fr,frmid,rarea);
}
int main()
{
int i;
double l,r;
cin>>n>>alpha;
++n;alpha=1/tan(alpha);
for(i=1;i<=n;i++)
{
cin>>circles[i].x;
circles[i].x*=alpha;
circles[i].x+=circles[i-1].x;
}
for(i=1;i<n;i++)
cin>>circles[i].r;
for(i=1;i<=n;i++)
{
l=min(l,circles[i].x-circles[i].r);
r=max(r,circles[i].x+circles[i].r);
}
for(i=2;i<=n;i++)
{
double L = circles[i].x - circles[i-1].x ;
if( L - fabs( circles[i-1].r - circles[i].r ) < eps )
continue;
double sin_alpha=( circles[i-1].r - circles[i].r ) / L ;
double cos_alpha=sqrt( 1 - sin_alpha * sin_alpha );
lines[++tot]=line( circles[i-1].x + circles[i-1].r * sin_alpha , circles[i-1].r * cos_alpha ,
circles[i ].x + circles[i ].r * sin_alpha , circles[i ].r * cos_alpha );
lines[tot].Get_Function();
}
double mid=(l+r)/2;
double fl=f(l);
double fr=f(r);
double fmid=f(mid);
printf("%.2lf\n", 2 * Get_Area( l , r , mid , fl , fr , fmid , Simpson(fl,fr,fmid,r-l) ) );
}