从PCA到Kernel PCA（Python）

PCA不进行分类的动作，而只做做数据预处理，将样本变换到一个容易分类（向最大化方差的方向，principal component axes，投影）的更低维的新的特征空间中。Kernel PCA比PCA多了一步，也即先升维（RBF包括多项式核均是升高到无穷维）再进行投影的动作，因为有些非线性可分的数据集只有在升维的视角下才线性可分。

PCA

• 均值化的数据：
  
  ∑ixi=0

# python 
>>> X-np.mean(X, 0)
                # 一个二维矩阵减去一维向量？对，
                # 这里用到的技术是numpy中broadcasting（广播机制）

• 样本协方差矩阵（sample-covariance matrix C ）
  

  C=1N∑ixixTi=1NXXT
  
  其中， X 的每一列表示一个样本（特征向量）

• 特征分解
  

  C=UΛUT=∑αλαuαuTα

• projection or transform

yi=UTkxi

1N∑iyiyTi=1N∑iUTkxixTiUk=UTk(1N∑ixixTi)Uk=UTkCUk=UTkUΛUUTk=Λk

the projected data are de-correlated in this new axis.

• 重构
  
  yi=UTkxi⇓Ukyi=UkUTkxi=xi

import pandas as pd
import numpy as np

df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data', header=None)
X, y = df.values[:, 1:], df.values[:, 0]

# step 1
X -= X.mean(0)

## step 2
N = X.shape[0]
C = X.T.dot(X)/N

## step 3
Lambda, Q = np.linalg.eig(C)

## step 4
k = 3
eigen_pairs = [(Lambda[i], Q[:, i]) for i in range(len(Lambda))]
eigen_pairs = sorted(eigen_pairs, reverse=True, key=lambda k: k[0])
W = np.column_stack((eigen_pairs[i][1] for i in range(k=3)))

## step 5
X_pca = X.dot(W)

Kernel PCA

以 Radial Basis Function（RBF） kernel PCA（不同的核，体现在代码上仅仅是一处细微的差别）为例进行说明：

• 计算核矩阵（相似度矩阵） K

Kij=k(x(i),x(j))=exp(−γ∥x(i)−x(j)∥2)

这是最为常见的RBF（Rational Basis Function）核函数，也有多项式核：

Kij=k(x(i),x(j))=(<x(i),x(j)>+θ)p

和 sigmoid型（hyperbolic tangent）核：

Kij=k(x(i),x(j))=tanh(η<x(i),x(j)>+θ)

其矩阵形式也即：

K=⎡⎣⎢⎢⎢⎢⎢⎢k(x(1),x(1)),k(x(2),x(1)),⋯,k(x(n),x(1)),k(x(1),x(2)),k(x(2),x(2)),⋯,k(x(n),x(2)),⋯,⋯,⋱,⋯,k(x(1),x(n))k(x(2),x(n))⋯k(x(n),x(n))⎤⎦⎥⎥⎥⎥⎥⎥n×n

• center the K

K′=K−1nK−K1n+1nK1n

其中 1n 是 n×n 的元素值全为 1n 矩阵。

• 对 K′ 进行特征值分解，获得对应于前 k 个特征值的特征向量。与标准PCA算法不同的是，这里获得特征向量不再是 principal component axes，而已经是全部样本在这些轴上的投影了，也即是我们所需的进行降维后的数据了。

这里为了验证核机制的性能，我们在如下的数据集上进行测试：

from sklearn.datasets import make_moons

X, y = make_moons(n_samples=200, random_state=123)
plt.scatter(X[y==0, 0], X[y==0, 1], colors='r', marker='^', alpha=.4)
plt.scatter(X[y==1, 0], X[y==1, 1], colors='b', marker='o', alpha=.4)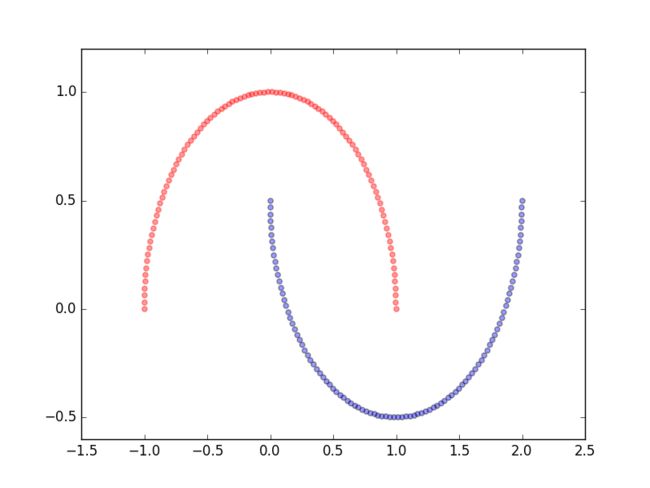

from scipy.spatial.distance import pdist, squareform

def rbf_kpca(X, gamma, k):
    sq_dist = pdist(X, metric='sqeuclidean')
                            # N = X.shape[0] 
                            # sq_dist.shape = N*(N-1)/2
    mat_sq_dist = squareform(sq_dist)
                            # mat_sq_dist.shape = (N, N)
    # step 1
    K = np.exp(-gamma*mat_sq_dist)

    # step 2
    N = X.shape[0]
    one_N = np.ones((N, N))/N
    K = K - one_N.dot(K) - K.dot(one_N) + one_N.dot(K).dot(one_N)

    # step 3
    Lambda, Q = np.linalg.eig(K)
    eigen_pairs = [(Lambda[i], Q[:, i]) for i in range(len(Lambda))]
    eigen_pairs = sorted(eigen_pairs, reverse=True, key=lambda k: k[0])
    return np.column_stack((eigen_pairs[i][1] for i in range(k)))

调用：

X_kpca = rbf_kpca(X, gamma=15, k=2)

一个非线性可分的数据集

from sklearn.datasets import make_circles
X, y = make_circles(n_samples=1000, noise=.1, factor=.2, random_state=123)
plt.scatter(X[y==0, 0], X[y==0, 1], color='r', marker='^', alpha=.4)
plt.scatter(X[y==1, 0], X[y==1, 1], color='b', marker='o', alpha=.4)
plt.show()

在这样的一个非线性可分的数据集，显然如何找到最大方差的方向都不可能使最后的数据集线性可分。接下来，我们探讨KPCA的核机制是如何工作的，使线性不可分的数据集变得线性可分，

应用kernel trick：

X_kpca = rbf_kpca(X, gamma=15, k=2)

可视化：

fig, ax = plt.subplots(1, 2, figsize=(8, 4))

ax[0].scatter(X_kpca[y==0, 0], X_kpca[y==0, 1], color='r', marker='^', alpha=.4)
ax[0].scatter(X_kpca[y==1, 0], X_kpca[y==1, 1], color='b', marker='o', alpha=.4)

label_count = np.bincount(y)
                                # 统计各类别出现的次数
                                # label_count[0] = 500
                                # label_count[1] = 500
ax[1].scatter(X_kpca[y==0, 0], np.zeros(label_count[0]), color='r')
ax[1].scatter(X_kpca[y==1, 0], np.zeros(label_count[1]), color='b')
                                # y轴置零
                                # 投影到x轴
ax[1].set_ylim([-1, 1])
ax[0].set_xlabel('PC1')
ax[0].set_ylabel('PC2')
ax[1].set_xlabel('PC1')

plt.show()

PCA 与 KPCA 的另一点重要不同

不同在于对新数据、新样本（当然还是同一类型数据，比如测试样本之于训练样本）的转换方式不同；

标准PCA算法，转换矩阵（transformation matrix Wd×k ）对应于训练样本的协方差矩阵的特征向量，使用 W 可继续作用于新的数据集， x′1×d⋅Wd×k 。而KPCA， K 的特征向量（ Ka=λα 中的 α ）即为变换后的样本。
对于新的样本，我们想要计算：

ϕ(x′)Tv

而特征向量 v=∑ia(i)ϕ(x(i)) ，则：

ϕ(x′)Tv=∑ia(i)ϕ(x′)Tϕ(x(i))=∑ia(i)k(x′,x(i))

from scipy.spatial.distance import sqdist, squareform

def rbf_kpca(X, gamma, k):
    sq_dists = sqdist(X, metric='sqeuclidean')
    mat_sq_dists = squareform(sq_dists)
    K = np.exp(-gamma*mat_sq_dists)
    N = X.shape[0]
    one_N = np.ones((N, N))/N
    K = K-one_N.dot(K)-K.dot(one_N)+one_N.dot(K).dot(one_N)
    Lambda, Q = np.linalg.eigh(K)
    alphas = np.column_stack((Q[:, -i]for i in range(1, 1+k)))
    lambdas = [Lambda[-i] for i in range(1, k+1)]
    return alphas, lambdas

def proj_new(X_new, X, gamma, alphas, lambdas):
    k = np.exp(-gamma*np.sum((X-X_new)**2, 1))
    return k.dot(alphas/lambdas)
                                # alphas/lambdas，归一化后的alphas

X, y = make_moons(n_samples=100, random_state=123)
                                # 设置random_state，为了可重复性
alphas, lambdas = rbf_kpca(X, gamma=15, k=1)
X_new = X[25]
                    # 以当前样本的某一样本作为新的样本进行测试
X_proj = proj_new(X_new, X, gamma=15, alphas, lambdas)
print(alphas[25])
print(X_proj)
                    # [-0.07877284]
                    # [-0.07877284]