平面分拆的 Macmahon 公式
平面分拆指的是计数组合学中的一大类计数问题,这些问题的一个共同特点就是表述简单,但是解决起来很困难,且解法往往天马行空精彩绝伦,此外它们还与交错矩阵猜想、表示论、概率论等分支有着奇妙的联系。本文要介绍的是其中最简单的一个:受限制的平面分拆的 Macmahon 公式
平面分拆的 Macmahon 公式
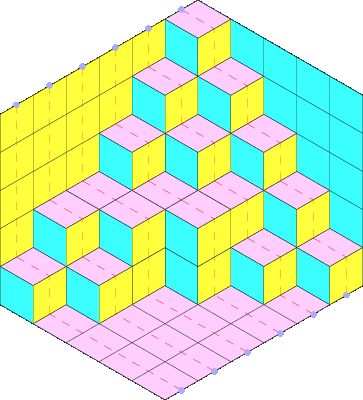
问题:一个边长为 $a\times b\times c$ 的平行六边形,每个内角都是 120 度。用边长为 1 的菱形铺砌,有多少种不同的方法?
下图是一种铺砌的示例:
我们观察这张图,发现它很像是在墙角 "堆箱子"(虽然它是个平面图形,但是我们想象在空间中鸟瞰它)。不仅如此,箱子的堆放方式还满足一个规律:从里到外,箱子的高度是递减的。用准确的语言描述:设 $A$ 是一个 $a\times b$ 矩阵, 其元素 $a_{ij}$ 表示地面上第 $i$ 行第 $j$ 列处箱子的高度,则 $A$ 满足条件:
每一行从左到右,每一列从上到下,$A$ 的元素都是递减的;(于是 $a_{11}$ 必然是矩阵中最大的元素)
每个元素 $a_{ij}$ 是介于 $0$ 和 $c$ 之间的非负整数。(箱子的高度不能超过天花板的高度 $c$)
我们把这样的矩阵 $A$ 叫做一个受限制的平面分拆,参数为 $(a,b,c)$。在上面的例子中,对应的平面分拆的参数为 $(6,5,5)$:(习惯上空白位置的 0 不写出来)
\[A=\begin{matrix}5&4&3&2&1\\4&3&2&1&\\3&3&2&&\\2&2&&&\\2&1&&&\\1&&&&\end{matrix}.\]
反之每一个受限制的平面分拆都对应于一个堆箱子的方式,从而对应于六边形的一个菱形铺砌。于是我们就把开头的铺砌问题转化为平面分拆的计数问题:
满足如下两个条件的 $a\times b$ 矩阵有多少个?
元素都是 $[0,c]$ 之间的非负整数;
每一行从左到右,每一列从上到下都是递减的。
设答案为 $M(a,b,c)$,则我们有一个非常令人吃惊的表达式:
Macmahon 公式:\[M(a,b,c)=\prod_{i=1}^a\prod_{j=1}^b\prod_{k=1}^c\frac{i+j+k-1}{i+j+k-2}.\]
虽然问题看起来很初等,但是答案的复杂暗示我们它并不像看起来那么容易。接下来你会看到,用一个巧妙的方法可以把问题转化为求一个行列式的值。
不相交的路径组
我们知道在平面上从点 $(0,c)$ 出发,每次向右或者向下移动一个单位的距离,到达点 $(b,0)$ 的路径总数为 $\begin{pmatrix}b+c\\b\end{pmatrix}$,这样的一条路径叫做 Gauss 路径。
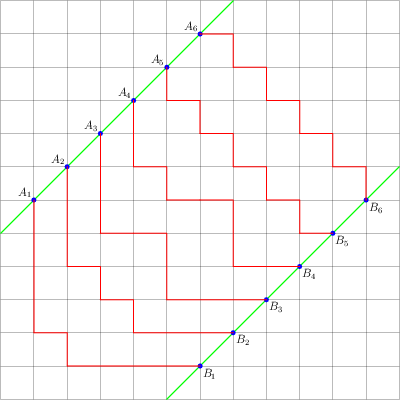
设 $A$ 是一个受限制的平面分拆,其参数 $(a,b,c)$ 的含义如前文所述,把 $A$ 的每一行的高度图投影到绿色的墙壁上,就得到了一条从 $(0,c)$ 到 $(b,0)$ 的 Gauss 路径,一共有 $a$ 条这样的路径:
但是平面分拆的列要满足递降关系,这个递降关系反映在路径上就是第二行对应的路径应该位于第一行对应的路径的下方(可以有交点),而第三行对应的路径又位于第二行对应的路径的下方,依此类推。
接下来是关键的一步: 如果把第一行对应的路径整体向右上方平移 $a$ 个单位,第二行对应的路径整体向右上方平移 $a-1$ 个单位,... ,第 $a$ 行对应的路径整体向右上方平移 1 个单位,则得到的 $a$ 条平移后的路径两两之间将没有任何公共点。我们称之为一个不相交的路径组。效果如下图所示:
这里 $A_i=(i,c+i)$,$B_j=(b+j,j)$,$\{p_i:A_i\rightarrow B_i,1\leq i\leq a\}$ 是一个不相交的路径组。反过来对每一个这样的不相交的路径组,你也可以很容易地写出对应的平面分拆来。
于是我们的问题又进一步转化为
设 $\{A_i=(i,c+i),1\leq i\leq a\}$ 和 $\{B_j=(b+j,j),1 \leq j\leq a\}$ 是平面上两组顶点集,求出所有不相交的路径组 $\mathcal{P}=\{p_i,1\leq i\leq a\}$ 的数目,其中 $p_i$ 是从 $A_i$ 出发到 $B_i$ 的 Gauss 路径。
Gessel - Viennot 的巧妙方法
考虑这样一个 $a\times a$ 的矩阵 $M$,其元素 $m_{ij}$ 就定义为从点 $A_i$ 出发到达点 $B_j$ 的所有 Gauss 路径的数目。由于点 $A_i$ 坐标为 $(i,c+i)$,点 $B_j$ 坐标为 $(b+j,j)$,不难得到这个数目是 $\begin{pmatrix}b+c\\b+i-j\end{pmatrix}$。这里如果 $b+i-j<0$ 则 $\begin{pmatrix}b+c\\b+i-j\end{pmatrix}=0$。Gessel - Viennot 引理非常意外地告诉我们:
Gessel - Viennot 引理:顶点集合 $\{A_i,1\leq i\leq a\}$ 和 $\{B_j,1\leq j\leq a\}$ 之间的不相交路径组的个数恰好为
\[\det M=\det_{1\leq i,j\leq a}\left(\left(\begin{array}{c}b+c\\b+i-j\end{array}\right)\right).\]
Gessel - Viennot 引理对更一般的图也成立,它在许多组合问题中都有精彩的应用。关于这方面可以参看 Aigner 的书 "proofs from the book" 以及 Stanley 的 "enumerative combinatorics"。
证明是非常之简洁的。把 $\det M$ 按照行列式的定义展开:
\[\begin{align*}\det M&=\sum_{\sigma}\text{sign}(\sigma)m_{ij}\\&=\sum_{\sigma}\text{sign}(\sigma)\left(\sum_{p_1:A_1\to B_{\sigma(1)}}1\right)\cdots\left(\sum_{p_a:A_a\to B_{\sigma(a)}}1\right).\end{align*}\]
现在我们取出其中的一项
\[\left(\sum_{p_1:A_1\to B_{\sigma(1)}}1\right)\cdots\left(\sum_{p_a:A_a\to B_{\sigma(a)}}1\right),\]
把它展开得到很多个 1 的和,每个 1 对应于一个路径组 $\mathcal{P}_\sigma=\{p_i,1\leq i\leq a\}$ ,这里 $p_i: A_i\rightarrow B_{\sigma(i)}$。因此这个和就是所有对应置换 $\sigma$ 的路径组 $\mathcal{P}_\sigma$ 的个数,从而
\[\det M=\sum_{\sigma,\mathcal{P}_\sigma}\text{sign}(\sigma).\]
我们要证明在上面的求和中所有相交的路径组对应的和项是可以两两配对抵消的,剩下的只有不相交的路径组,而不相交的路径组只有在 $\sigma$ 为恒等置换时才可能发生(从图上可以很容易看出这一点,如果 $\sigma$ 不是恒等置换,则路径组 $\mathcal{P}_\sigma$ 中必有相交的路径)。这样就得到 $\det M=\sum\limits_{\mathcal{P}}1$,而且 $\mathcal{P}$ 只跑遍满足每个路径都是从 $A_i$ 到 $B_i$ 的不相交路径组,这就是所求的答案。
对每一个相交的路径组 $\mathcal{P}_\sigma$, 我们要找另一个与之配对的 $\mathcal{P}_{\sigma'}$,使得 $\text{sign}(\sigma)=-\text{sign}(\sigma')$,则这二者对应的和项就抵消掉了。这一步很容易:在 $\mathcal{P}_\sigma$ 的所有交点中, 我们找出位于 "最东北" 方向的那一个, 这个点是唯一确定的一个,记作 $C$。当然可能有好几条路径(多于 2 条)都经过 $C$ 点,为此我们选择最大的 $i$ 使得 $p_i:A_i\rightarrow B_{\sigma(i)}$ 经过 $C$,再选择最大的 $j,j<i$ 使得 $p_j:A_j\rightarrow B_{\sigma(j)}$ 经过 $C$。
现在我们构造 $\mathcal{P}_{\sigma'}$ 如下:交换 $p_i$ 和 $p_j$ 在 $C$ 点之后的部分,保持其它 $p_k$ 不动。
(想象两个人分别从 $A_i$ 和 $A_j$ 出发沿着路径 $p_i$ 和 $p_j$ 前往目的地 $B_{\sigma(i)}$ 和 $B_{\sigma(j)}$。当他们在点 $C$ 相遇时,强迫他们改变路线,沿着对方剩下的路径前往对方的目的地)
于是在 $\mathcal{P}_{\sigma'}$ 中有 $p_i':A_i\rightarrow B_{\sigma(j)}$,$p_j':A_j\rightarrow B_{\sigma(i)}$。显然置换 $\sigma'$ 与 $\sigma$ 只差一个对换 $(ij)$,因此符号相反。更重要的是如果对 $\mathcal{P}_{\sigma'}$ 也进行这个变换的话,又回到了 $\mathcal{P}_\sigma$(这一点很重要,这才能保证是名符其实的 "两两配对"),因此它们对应的和项抵消,这就证明了结论。
Dodgson's condensation method
为了求出行列式的值,我们介绍一个古老的方法:Dodgson's condensation。这是一个递归求解行列式的方法:设 $A$ 是一个 $n\times n$ 矩阵,用 $A_i^j$ 表示删去 $A$ 的第 $i$ 行和第 $j$ 列后剩下的 $n-1$ 阶矩阵,用 $A_{1,n}^{1,n}$ 表示删去 $A$ 的第 1 行第 1 列和第 $n$ 行第 $n$ 列后剩下的 $n-2$ 阶矩阵,则我们有恒等式
\[ \det A\cdot \det A_{1,n}^{1,n}=\det A_1^1\det A_n^n-\det A_1^n\det A_n^1.\]
这个结论的证明不难,可以见维基百科,这里就不再照抄一遍了。
我们对 $a$ 归纳来证明
Macmahon 公式:\[\det_{1\leq i,j\leq a}\left(\left(\begin{array}{c}b+c\\b+i-j\end{array}\right)\right)=\prod_{i=1}^a\prod_{j=1}^b\prod_{k=1}^c\frac{i+j+k-1}{i+j+k-2}.\]
首先你需要对 $a=1$ 和 $a=2$ 的情形手算验证(略繁琐,不过只是一个 2 阶矩阵),设 $M_a(b,c)$ 为所求的行列式,注意到
\[\left\{\begin{array}{l}(M_a(b,c))_1^1=M_{a-1}(b,c),\\(M_a(b,c))_n^n=M_{a-1}(b,c),\\(M_a(b,c))_1^n=M_{a-1}(b-1,c+1),\\(M_a(b,c))_n^1=M_{a-1}(b+1,c-1),\\(M_a(b,c))^{1,n}_{1,n}=M_{a-2}(b,c).\end{array}\right.\]
然后应用归纳假设即可。
这个行列式的求法不是唯一的,不过 Dodgson 的方法是最好的。你可能怀疑这么笨拙的方法居然还能称得上是好方法。实际上在组合行列式的领域,复杂的行列式比比皆是,有的行列式甚至光把答案写出来都要占半页纸。想靠人的大脑凭借奇思妙想几下解出来非常困难。相比之下 Dodgson 算法则直接了当,只要找到递推关系,剩下的事情交给计算机即可。
番外话
说点八卦的东西。Dodgson 是 19 世纪英国牛津大学的数学教授,细心点的读者可能注意到这位老兄的名字实在让人不敢恭维:Dodgson,dog ... son?大概他也知道自己的名字难登大雅之堂,所以他给自己取了一个很好听的笔名:Lewis Carroll。
你对这个名字没有反应么?那好,我们继续说说他的轶事。这位老兄虽然名字略俗,受过的教育可不含糊,也算上层社会体面人物。但是按照今天的话说,是个不折不扣的怪蜀黍,对萝莉有着特别的喜爱,尤其喜爱给她们拍裸照,这一点和冠希哥趣味相投,所以后人基本认定他是一个恋童癖大叔。他曾经专门为邻居家的女儿写了一部童话来哄她开心,这就是大名鼎鼎的 "艾丽斯漫游奇境记"。虽然创作动机不纯,但是这部童话非常精彩,以至于当时的英国女王都变成了他的粉丝。女王命令手下的大臣把 Dodgson 的全部著作都搜集呈上来,于是大臣献上了一本厚厚的 "符号逻辑",当然结果你猜得到的 ...
时光一转到了 20 世纪 80 年代,三位数学家 William Mills,David Robbins 和 Howard Rumsey 在研究计算行列式的快速数值算法时,受 Dodgson 算法的启发,发现了交错符号矩阵猜想。这是计数组合学里面最重要的猜想之一,堪称组合数学中 “皇冠上的明珠”。我向你推荐 Bressoud 的书 “Proofs and Confirmations: the story of the alternating sign matrix conjecture“,我保证里面的故事和 "爱丽丝漫游奇境记" 一样奇妙 ...