贪心算法(2)-Kruskal最小生成树

原文地址 http://www.acmerblog.com/greedy-kruskal-spanning-tree-mst-5326.html

参考地址 http://www.geeksforgeeks.org/greedy-algorithms-set-2-kruskals-minimum-spanning-tree-mst/

什么是最小生成树？

生成树是相对图来说的，一个图的生成树是一个树并把图的所有顶点连接在一起。一个图可以有许多不同的生成树。一个有 n 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边。最小生成树其实是最小权重生成树的简称。生成树的权重是考虑到了生成树的每条边的权重的总和。

最小生成树有几条边？

最小生成树有（V – 1）条边，其中V是给定的图的顶点数量。

Kruskal算法

下面是步骤寻找MST使用Kruskal算法

1 1，按照所有边的权重排序(从小到大)
2
3 2，选择最小的边。检查它是否形成与当前生成树形成环。如果没有形成环，讲这条边加入生成树。否则，丢弃它。
4
5 3，重复第2步，直到有生成树（V-1）条边

步骤2使用并查集算法来检测环。如果不熟悉并查集建议阅读下并查集。

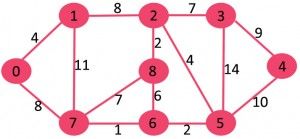
该算法是一种贪心算法。贪心的选择是选择最小的权重的边，并不会和当前的生成树形成环。让我们了解一个例子，考虑下面输入图

spanning-tree-mst

该图包含9个顶点和14个边。因此，形成最小生成树将有（9 – 1）= 8条边。

01 排序后：
02 Weight   Src    Dest
03 1         7      6
04 2         8      2
05 2         6      5
06 4         0      1
07 4         2      5
08 6         8      6
09 7         2      3
10 7         7      8
11 8         0      7
12 8         1      2
13 9         3      4
14 10        5      4
15 11        1      7
16 14        3      5

现在从已经排序的边中逐个选择

1. Pick edge 7-6: No cycle is formed, include it.

2. Pick edge 8-2: No cycle is formed, include it.

3. Pick edge 6-5: No cycle is formed, include it.

4. Pick edge 0-1: No cycle is formed, include it.

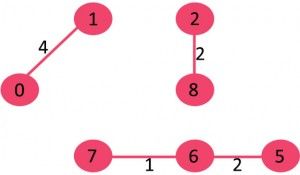
5. Pick edge 2-5: No cycle is formed, include it.

6. Pick edge 8-6: Since including this edge results in cycle, discard it.

7. Pick edge 2-3: No cycle is formed, include it.

8. Pick edge 7-8: Since including this edge results in cycle, discard it.

9. Pick edge 0-7: No cycle is formed, include it.

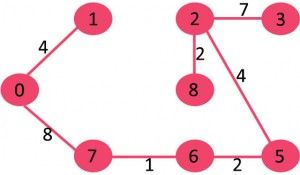
10. Pick edge 1-2: Since including this edge results in cycle, discard it.

11. Pick edge 3-4: No cycle is formed, include it.

目前为止一家有了 V-1 条边，可以肯定V个顶点都一包含在内，到此结束。

代码实现：

001 // Kruskal 最小生成树算法
002 #include <stdio.h>
003 #include <stdlib.h>
004 #include <string.h>
005
006 // 带有权重的边
007 struct Edge
008 {
009     int src, dest, weight;
010 };
011
012 // 无向图
013 struct Graph
014 {
015     // V-> 顶点个数, E->边的个数
016     int V, E;
017     // 由于是无向图，从 src 到 dest的边，同时也是 dest到src的边，按一条边计算
018     struct Edge* edge;
019 };
020
021 //构建一个V个顶点 E条边的图
022 struct Graph* createGraph(int V, int E)
023 {
024     struct Graph* graph = (struct Graph*) malloc( sizeof(struct Graph) );
025     graph->V = V;
026     graph->E = E;
027     graph->edge = (struct Edge*) malloc( graph->E * sizeof( struct Edge ) );
028     return graph;
029 }
030
031 //并查集的结构体
032 struct subset
033 {
034     int parent;
035     int rank;
036 };
037
038 // 使用路径压缩查找元素i
039 int find(struct subset subsets[], int i)
040 {
041     if (subsets[i].parent != i)
042         subsets[i].parent = find(subsets, subsets[i].parent);
043
044     return subsets[i].parent;
045 }
046
047 // 按秩合并 x，y
048 void Union(struct subset subsets[], int x, int y)
049 {
050     int xroot = find(subsets, x);
051     int yroot = find(subsets, y);
052     if (subsets[xroot].rank < subsets[yroot].rank)
053         subsets[xroot].parent = yroot;
054     else if (subsets[xroot].rank > subsets[yroot].rank)
055         subsets[yroot].parent = xroot;
056     else
057     {
058         subsets[yroot].parent = xroot;
059         subsets[xroot].rank++;
060     }
061 }
062
063 // 很据权重比较两条边
064 int myComp(const void* a, const void* b)
065 {
066     struct Edge* a1 = (struct Edge*)a;
067     struct Edge* b1 = (struct Edge*)b;
068     return a1->weight > b1->weight;
069 }
070
071 // Kruskal 算法
072 void KruskalMST(struct Graph* graph)
073 {
074     int V = graph->V;
075     struct Edge result[V];  //存储结果
076     int e = 0;  //result[] 的index
077     int i = 0;  // 已排序的边的 index
078
079     //第一步排序
080     qsort(graph->edge, graph->E, sizeof(graph->edge[0]), myComp);
081
082     // 为并查集分配内存
083     struct subset *subsets =
084         (struct subset*) malloc( V * sizeof(struct subset) );
085
086     // 初始化并查集
087     for (int v = 0; v < V; ++v)
088     {
089         subsets[v].parent = v;
090         subsets[v].rank = 0;
091     }
092
093     // 边的数量到V-1结束
094     while (e < V - 1)
095     {
096         // Step 2: 先选最小权重的边
097         struct Edge next_edge = graph->edge[i++];
098
099         int x = find(subsets, next_edge.src);
100         int y = find(subsets, next_edge.dest);
101
102         // 如果此边不会引起环
103         if (x != y)
104         {
105             result[e++] = next_edge;
106             Union(subsets, x, y);
107         }
108         // 否则丢弃，继续
109     }
110
111     // 打印result[]
112     printf("Following are the edges in the constructed MST\n");
113     for (i = 0; i < e; ++i)
114         printf("%d -- %d == %d\n", result[i].src, result[i].dest,
115                                                    result[i].weight);
116     return;
117 }
118
119 // 测试
120 int main()
121 {
122     /* 创建下面的图：
123              10
124         0--------1
125         |  \     |
126        6|   5\   |15
127         |      \ |
128         2--------3
129             4       */
130     int V = 4;  // 顶点个数
131     int E = 5;  //边的个数
132     struct Graph* graph = createGraph(V, E);
133     // 添加边 0-1
134     graph->edge[0].src = 0;
135     graph->edge[0].dest = 1;
136     graph->edge[0].weight = 10;
137
138     graph->edge[1].src = 0;
139     graph->edge[1].dest = 2;
140     graph->edge[1].weight = 6;
141
142     graph->edge[2].src = 0;
143     graph->edge[2].dest = 3;
144     graph->edge[2].weight = 5;
145
146     graph->edge[3].src = 1;
147     graph->edge[3].dest = 3;
148     graph->edge[3].weight = 15;
149
150     graph->edge[4].src = 2;
151     graph->edge[4].dest = 3;
152     graph->edge[4].weight = 4;
153
154     KruskalMST(graph);
155
156     return 0;
157 }

结果如下：

1 Following are the edges in the constructed MST
2 2 -- 3 == 4
3 0 -- 3 == 5
4 0 -- 1 == 10

 时间复杂度：

O(ElogE) 或 O(ElogV)。 排序使用 O(ELogE) 的时间，之后我们遍历中使用并查集O(LogV) ，所以总共复杂度是 O(ELogE + ELogV)。E的值最多为V^2，所以

O(LogV) 和 O(LogE) 可以看做是一样的。