第三章信息编码与数据表示(一)
第三章信息编码与数据表示
一.进位计数值
基本概念
基数R
指在这种进位制中允许使用的基本数码个数。基数为R的数制称为R进制数。 R进制数的主要特点就是逢R进1
权Wi
权也称位权,指某一位i上的数码的权重值,即权与数码所处的位置i有关。 Wi =Ri。
假设任意数值N用R进制数来表示,形式为:
N=(Dm-1Dm-2…D0 .D-1D-2 …D-k )R
其中,Di为该进制的基本符号,Di∈[0,R-1],i = -k, -k+1, ……,m-1;小数点在D0和D-1之间。
(11011.011)2=1×24+ 1×23+ 0×22+1×21+ 1×2-0+ 0×2-1 + 1×2-2 + 1×2-3=(27.375)10
(2345.459)10=2×103+ 3×102+ 4×101+5×100+ 4×10-1+ 5×10-2+ 9×10-3
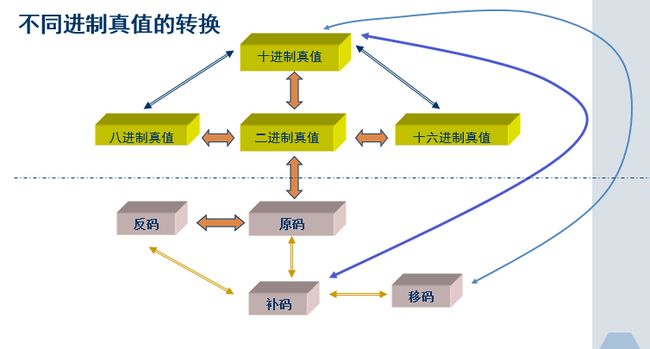
二.不同进制转换
常见的进制###:
十进制(Decimal)、二进制(Binary)、八进制(Octal)、十六进制(Hexdecimal)数分别用D、B、Q、H来标志。
* 实例*
(2B.D)16=(2B.D)H=(43.8125)10=(53.64)Q
其他进制转化为十进制:
实例
(5AC.E6)16= 5×162+ 10×161 +12×160 +14×16-1+ 6×16-2 =(1452.8984375)10
十进制变二进制,八进制,十六进制:
转换方法:可以分为以下两种方法
直接转换:十进制→二、八、十六进制
间接转换:十进制→二进制→ 八、十六进制
- 十进制→R进制
转换方法
整数部分:除以R取余,先得低位,直到商为0。
小数部分:乘R取整,先得高位,直到积为0或者达到精度要求为止。
实例:

(123.75)10=( 173.6 )8
当小数部分不能整除为二进制时,则乘以2取整的过程中,积不会为0;或者当小数部分转化为二进制位数很长,这时由精度来决定二进制位数。
若要求精度大于10%,则表示“=”左右两边的十进制值的差的绝对值<10%。
即,10%>2-n
所以 n=4
- 二进制→八,十六进制
二进制→八进制
以小数点为中心分别向两边分组,每三位一组,写出对应的八进制数字。(不够位数则在两边加0补足3位 )
二进制→十六进制
以小数点为中心分别向两边分组,每四位一组,写出对应的十六进制符号。(不够位数则在两边加0补足4位 )
实例
(1011111.11)2=( 137.6 )8=( 5F.C )16 - 八进制→二进制
将每位八进制数展开为3位二进制数,最高位和最低位的0可以略去。 - 十六进制→二进制:
将每位十六进制数展开为4位二进制数,最高位和最低位的0可以略去。
实例
(765.23)8=( 111 110 101.010 011 )2
(765.23)16=( 111 0110 0101.0010 0011 )2
计算机中为什么采用二进制表示数据?
1. 具有二值状态的物理器件容易实现。
2. 二进制的运算规则简单,硬件实现容易。
3. 具有逻辑特性,可代表“真假”、“是非”。
4. 抗干扰能力强、可靠性高
三.十进制数的编码
如何在计算机内使用二进制来表示十进制数据?
(1)二-十进制码(BCD码)
(2)十进制数串的表示方法
BCD(Binary Coded Decimal)码:
使用二进制来编码十进制数字0~9。
编码方法:
一般使用4位二进制编码来表示1位十进制数字,在16个编码中选用10个来表示数字0~9。不同的选择构成不同的BCD码 。
分类:
- 有权码:
编码的每一位都有固定的权值,加权求和的值即是表示的十进制数字。如8421码、2421码、5211码、4311码、84 -2-1码等。
- 无权码:
十进制数串的表示方法
字符串形式:
用ASCII码来表示十进制数字或符号位,即1个字节存放1位十进制数字或符号位。
压缩的十进制数串形式:
用BCD码来表示十进制数字,即1个字节存放2个十进制的数字;符号位放在最低位数字位之后,一般用C(12)表示正号,用D(13)表示负号。
例如 +258被表示成258CH,占用两个字节,-34被表示为034DH,也占用两个字节。
共同点:
必须给出它在主存中的首地址和位长
采用十进制表示数据的优点是:
对于需要大量地进行输入输出数据而运算简单的场合,大大减少了十→二和二→十转换,提高了机器的运行效率;
十进制数串的位长可变,许多机器中规定该长度从0到31,有的甚至更长。不受定点数和浮点数统一格式的约束,从而提高了数据的表示范围和运算精度。
数据格式
计算机中参与运算的数据有两种:
无符号数据( Unsigned )
所有的二进制数据位数均用来表示数值本身,没有正负之分。带符号数据( Signed)
二进制数据位,包括符号位和数值位。计算机中的带符号数据又称为机器数。
机器数
把“+”、“-”符号代码化,并保存在计算机中的数据。
机器数的特点:
- 机器数的表示范围受计算机机器字长的限制。
- 符号必须数值化。
- 机器数的小数点是用规定的隐含方式表达的。
真值:
是指机器数所真正表示的数值,用数值并冠以“+”、“-”符号的方法来表示。
机器数的编码方法
:原码、反码、补码、移码。
计算机硬件如何区分它们是无符号数据还是带符号数据的呢?
根据执行不同的指令
小数点的表示方法
在机器数中,小数点及其位置是隐含规定的;有两种隐含方式:
定点数:小数点的位置是固定不变的
浮点数:小数点的位置是浮动的
定点机器数分为定点小数、定点整数两种。
浮点机器数中小数点的位置由阶码规定,因此是浮动的。
定点机器数的小数点的位置是固定不变的,可以分为两种:
定点小数:用于表示纯小数,小数点隐含固定在最高数据位的左边,整数位则用于表示符号位。
定点整数:用于表示纯整数,小数点位置隐含固定在最低位之后,最高位为符号位。
原码表示法
表示方法:
最高位表示数的符号,其他位表示数值位。
符号位:
0——正数,1——负数。
数值位:
与绝对值相同。
实例
例1:X=1011,Y=-1011,则:
[X]原=0,1011 ; [Y]原= 1,1011 ;
例2:X=0.1101,Y=- 0.1101,则:
[X]原=0.1101 ;[Y]原= 1.1101 ;
例3: X=1011, Y=- 0.1101,求X和Y的8位原码机器数。
[X]原=0,0001011 ;[Y]原= 1.1101000 ;
0 的表示:
0 的原码表示有两种形式,即分别按照正数和负数表示。
[+0]原= 00…0 [-0]原= 10…0
表示范围:对于n+1位原码机器数X,它所能表示的数据范围为:
定点整数:-(2^n-1)≤X ≤ 2^n-1
定点小数:-(1-2^-n)≤X ≤ 1-2^-n
溢出:当机器遇到一个超出它的机器数表示范围的数据
反码表示
表示方法:
最高位表示数的符号,其他位表示数值位。
符号位:
0-正数,1-负数。
数值位:
正数时,与绝对值相同;负数时,为绝对值取反。
X=1011,Y=-1011,则:
[X]反= 0,1011 ;[Y]反=1,0100 ;
例2:X=0.1101,Y=- 0.1101,则:
[X]反=0.1101 ;[Y]反=1.0010 ;
例3: X=1011, Y=- 0.1101,求X和Y的8位反码机器数。
[X]反=0,0001011 ;[Y]反=1.0010111 ;
0 的表示:
0 的反码表示有两种形式,即分别按照正数和负数表示。
[+0]反= 00…0 [-0]反= 11…1
表示范围:
对于n+1位反码机器数X,它所能表示的数据范围为:
定点整数:
-(2^n-1)≤X ≤ 2^n-1
定点小数:
-(1-2^-n)≤X ≤ 1-2^-n
补码表示
表示方法:
最高位为符号位,其他位为数值位。
符号位:
0-正数,1-负数。
数值位:
正数时,与绝对值相同;负数时,为绝对值取反后,末位加1。
简单算法:
负数时候,从后往前看,遇到第一个1,这个1以及以后的1后不变,前面求反。
实例
例1:X=1011,Y=-1011,则:
[X]补= 0,1011;[Y]补=1,0101;
例2:X=0.1101,Y=- 0.1101,则:
[X]补= 0.1101;[Y]补=1. 0011 ;
例3: X=1011, Y=- 0.1101,求X和Y的8位补码机器数。
[X]补= 0,0001011;[Y]补=1.0011000;
0 的表示:
0 的补码表示形式是唯一的,即分别按照正数和负数表示均一致,为全零。
[+0]补= 00…0 [-0]补= 00…0
表示范围:
对于n+1位补码机器数X,它所能表示的数据范围为:
定点整数:
-2^n≤X ≤ 2^n-1
定点小数:-1≤X ≤ 1-2^-n
计算机中的整型数据(int)均用补码来表示。
移码表示
表示方法:
最高位为符号位,其他位为数值位。
符号位:
1-正数,0-负数。
数值位:
正数时,与绝对值相同;负数时,为绝对值取反后,末位加1。
即即负数时候,为补码的符号位取反
实例
例1:X=1011,Y=-1011,则:
[X]移=1,1011 ;[Y]移=0,0101;
例2:X=0.1101,Y=- 0.1101,则:
[X]移= 1.1101 ;[Y]移= 0.0011 ;
例3: X=1011, Y=- 0.1101,求X和Y的8位移码机器数。
[X]移=1,00001011;[Y]移= 0.00110000 ;
0 的表示:
0 的移码表示形式是唯一的,即分别按照正数和负数表示均一致。
[+0]移= 10…0 [-0]移= 10…0
表示范围:
对于n+1位移码机器数X,它所能表示的数据范围为:
定点整数:
-2^n ≤X ≤ 2^n-1
定点小数:
-1≤X ≤ 1-2^-n
移码通常作为浮点数的阶码,一般只用来表示定点整数。
定点机器数转换
机器数转换为真值
四种定点机器数转换为真值的方法要点是:
首先根据机器数的符号位确定真值的正负,然后对照机器数的定义和表示,反方向求出真值的绝对值
机器数之间的相互转换
原码、补码、反码和移码之间的相互转换,最简单的方法是先求出它们的真值,然后再转换为另一种表示方法。