C语言中整型溢出的危害
整型溢出有点老生常谈了,但似乎没有引起多少人的重视。整型溢出会有可能导致缓冲区溢出,缓冲区溢出会导致各种黑客攻击。在这里写下这篇文章,希望大家都了解一下整型溢出,编译器的行为,以及如何防范,以写出更安全的代码。
什么是整型溢出
C语言的整型问题相信大家并不陌生了。对于整型溢出,分为无符号整型溢出和有符号整型溢出。
对于unsigned整型溢出,C的规范是有定义的——“溢出后的数会以2^(8*sizeof(type))作模运算”,也就是说,如果一个unsigned char(1字符,8bits)溢出了,会把溢出的值与256求模。例如:
|
1
2
|
unsigned
char
x = 0xff;
printf
(
"%d\n"
, ++x);
|
上面的代码会输出:0 (因为0xff + 1是256,与2^8求模后就是0)
对于signed整型的溢出,C的规范定义是“undefined behavior”,也就是说,编译器爱怎么实现就怎么实现。对于大多数编译器来说,算得啥就是啥。比如:
|
1
2
|
signed
char
x =0x7f;
//注:0xff就是-1了,因为最高位是1也就是负数了
printf
(
"%d\n"
, ++x);
|
上面的代码会输出:-128,因为0x7f + 0x01得到0x80,也就是二进制的1000 0000,符号位为1,负数,后面为全0,就是负的最小数,即-128。
另外,千万别以为signed整型溢出就是负数,这个是不定的。比如:
|
1
2
3
4
|
signed
char
x = 0x7f;
signed
char
y = 0x05;
signed
char
r = x * y;
printf
(
"%d\n"
, r);
|
上面的代码会输出:123
相信对于这些大家不会陌生了。
整型溢出的危害
下面说一下,整型溢出的危害。
示例一:整形溢出导致死循环
|
1
2
3
4
5
6
7
8
|
... ...
... ...
short
len = 0;
... ...
while
(len< MAX_LEN) {
len += readFromInput(fd, buf);
buf += len;
}
|
上面这段代码可能是很多程序员都喜欢写的代码(我在很多代码里看到过多次),其中的MAX_LEN 可能会是个比较大的整型,比如32767,我们知道short是16bits,取值范围是-32768 到 32767 之间。但是,上面的while循环代码有可能会造成整型溢出,而len又是个有符号的整型,所以可能会成负数,导致不断地死循环。
示例二:整形转型时的溢出
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
int
copy_something(
char
*buf,
int
len)
{
#define MAX_LEN 256
char
mybuf[MAX_LEN];
... ...
... ...
if
(len > MAX_LEN){
// <---- [1]
return
-1;
}
return
memcpy
(mybuf, buf, len);
}
|
上面这个例子中,还是[1]处的if语句,看上去没有会问题,但是len是个signed int,而memcpy则需一个size_t的len,也就是一个unsigned 类型。于是,len会被提升为unsigned,此时,如果我们给len传一个负数,会通过了if的检查,但在memcpy里会被提升为一个正数,于是我们的mybuf就是overflow了。这个会导致mybuf缓冲区后面的数据被重写。
示例三:分配内存
关于整数溢出导致堆溢出的很典型的例子是,OpenSSH Challenge-Response SKEY/BSD_AUTH 远程缓冲区溢出漏洞。下面这段有问题的代码摘自OpenSSH的代码中的auth2-chall.c中的input_userauth_info_response() 函数:
|
1
2
3
4
5
6
|
nresp = packet_get_int();
if
(nresp > 0) {
response = xmalloc(nresp*
sizeof
(
char
*));
for
(i = 0; i < nresp; i++)
response[i] = packet_get_string(NULL);
}
|
上面这个代码中,nresp是size_t类型(size_t一般就是unsigned int/long int),这个示例是一个解数据包的示例,一般来说,数据包中都会有一个len,然后后面是data。如果我们精心准备一个len,比如:1073741825(在32位系统上,指针占4个字节,unsigned int的最大值是0xffffffff,我们只要提供0xffffffff/4 的值——0x40000000,这里我们设置了0x4000000 + 1), nresp就会读到这个值,然后nresp*sizeof(char*)就成了 1073741825 * 4,于是溢出,结果成为了 0x100000004,然后求模,得到4。于是,malloc(4),于是后面的for循环1073741825 次,就可以干环事了(经过0x40000001的循环,用户的数据早已覆盖了xmalloc原先分配的4字节的空间以及后面的数据,包括程序代码,函数指针,于是就可以改写程序逻辑。关于更多的东西,你可以看一下这篇文章《Survey of Protections from Buffer-Overflow Attacks》)。
示例四:缓冲区溢出导致安全问题
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
int
func(
char
*buf1, unsigned
int
len1,
char
*buf2, unsigned
int
len2 )
{
char
mybuf[256];
if
((len1 + len2) > 256){
//<--- [1]
return
-1;
}
memcpy
(mybuf, buf1, len1);
memcpy
(mybuf + len1, buf2, len2);
do_some_stuff(mybuf);
return
0;
}
|
上面这个例子本来是想把buf1和buf2的内容copy到mybuf里,其中怕len1 + len2超过256 还做了判断,但是,如果len1+len2溢出了,根据unsigned的特性,其会与2^32求模,所以,基本上来说,上面代码中的[1]处有可能为假的。(注:通常来说,在这种情况下,如果你开启-O代码优化选项,那个if语句块就全部被和谐掉了——被编译器给删除了)比如,你可以测试一下 len1=0x104, len2 = 0xfffffffc 的情况。
示例五:size_t 的溢出
|
1
|
for
(
int
i=
strlen
(s)-1; i>=0; i--) { ... }
|
|
1
|
for
(
int
i=v.size()-1; i>=0; i--) { ... }
|
上面这两个示例是我们经常用的从尾部遍历一个数组的for循环。第一个是字符串,第二个是C++中的vector容器。strlen()和vector::size()返回的都是 size_t,size_t在32位系统下就是一个unsigned int。你想想,如果strlen(s)和v.size() 都是0呢?这个循环会成为个什么情况?于是strlen(s) – 1 和 v.size() – 1 都不会成为 -1,而是成为了 (unsigned int)(-1),一个正的最大数。导致你的程序越界访问。
这样的例子有很多很多,这些整型溢出的问题如果在关键的地方,尤其是在搭配有用户输入的地方,如果被黑客利用了,就会导致很严重的安全问题。
关于编译器的行为
在谈一下如何正确的检查整型溢出之前,我们还要来学习一下编译器的一些东西。请别怪我罗嗦。
编译器优化
如何检查整型溢出或是整型变量是否合法有时候是一件很麻烦的事情,就像上面的第四个例子一样,编译的优化参数-O/-O2/-O3基本上会假设你的程序不会有整形溢出。会把你的代码中检查溢出的代码给优化掉。
关于编译器的优化,在这里再举个例子,假设我们有下面的代码(又是一个相当相当常见的代码):
|
1
2
3
4
5
6
7
|
int
len;
char
* data;
if
(data + len < data){
printf
(
"invalid len\n"
);
exit
(-1);
}
|
上面这段代码中,len 和 data 配套使用,我们害怕len的值是非法的,或是len溢出了,于是我们写下了if语句来检查。这段代码在-O的参数下正常。但是在-O2的编译选项下,整个if语句块被优化掉了。
你可以写个小程序,在gcc下编译(我的版本是4.4.7,记得加上-O2和-g参数),然后用gdb调试时,用disass /m命信输出汇编,你会看到下面的结果(你可以看到整个if语句块没有任何的汇编代码——直接被编译器和谐掉了):
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
7 int len = 10;
8 char* data = (char *)malloc(len);
0x00000000004004d4 <+4>: mov $0xa,%edi
0x00000000004004d9 <+9>: callq 0x4003b8 <malloc@plt>
9
10
if
(data + len < data){
11
printf
(
"invalid len\n"
);
12
exit
(-1);
13 }
14
15 }
0x00000000004004de <+14>: add $0x8,%rsp
0x00000000004004e2 <+18>: retq
|
对此,你需要把上面 char* 转型成 uintptr_t 或是 size_t,说白了也就是把char*转成unsigned的数据结构,if语句块就无法被优化了。如下所示:
|
1
2
3
|
if
((
uintptr_t
)data + len < (
uintptr_t
)data){
... ...
}
|
关于这个事,你可以看一下C99的规范说明《 ISO/IEC 9899:1999 C specification 》第 §6.5.6 页,第8点,我截个图如下:(这段话的意思是定义了指针+/-一个整型的行为,如果越界了,则行为是undefined)
注意上面标红线的地方,说如果指针指在数组范围内没事,如果越界了就是undefined,也就是说这事交给编译器实现了,编译器想咋干咋干,那怕你想把其优化掉也可以。在这里要重点说一下,C语言中的一个大恶魔—— Undefined! 这里都是“野兽出没”的地方,你一定要小心小心再小心。
花絮:编译器的彩蛋
上面说了所谓的undefined行为就全权交给编译器实现,gcc在1.17版本下对于undefined的行为还玩了个彩蛋(参看Wikipedia)。
下面gcc 1.17版本下的遭遇undefined行为时,gcc在unix发行版下玩的彩蛋的源代码。我们可以看到,它会去尝试去执行一些游戏NetHack, Rogue 或是Emacs的 Towers of Hanoi,如果找不到,就输出一条NB的报错。
|
1
2
3
4
5
6
|
execl(
"/usr/games/hack"
,
"#pragma"
, 0);
// try to run the game NetHack
execl(
"/usr/games/rogue"
,
"#pragma"
, 0);
// try to run the game Rogue
// try to run the Tower's of Hanoi simulation in Emacs.
execl(
"/usr/new/emacs"
,
"-f"
,
"hanoi"
,
"9"
,
"-kill"
,0);
execl(
"/usr/local/emacs"
,
"-f"
,
"hanoi"
,
"9"
,
"-kill"
,0);
// same as above
fatal(
"You are in a maze of twisty compiler features, all different"
);
|
正确检测整型溢出
在看过编译器的这些行为后,你应该会明白——“在整型溢出之前,一定要做检查,不然,就太晚了”。
我们来看一段代码:
|
1
2
3
4
5
|
void
foo(
int
m,
int
n)
{
size_t
s = m + n;
.......
}
|
上面这段代码有两个风险:1)有符号转无符号,2)整型溢出。这两个情况在前面的那些示例中你都应该看到了。所以,你千万不要把任何检查的代码写在 s = m + n 这条语名后面,不然就太晚了。undefined行为就会出现了——用句纯正的英文表达就是——“Dragon is here”——你什么也控制不住了。(注意:有些初学者也许会以为size_t是无符号的,而根据优先级 m 和 n 会被提升到unsigned int。其实不是这样的,m 和 n 还是signed int,m + n 的结果也是signed int,然后再把这个结果转成unsigned int 赋值给s)
比如,下面的代码是错的:
|
1
2
3
4
5
6
7
|
void
foo(
int
m,
int
n)
{
size_t
s = m + n;
if
( m>0 && n>0 && (SIZE_MAX - m < n) ){
//error handling...
}
}
|
上面的代码中,大家要注意 (SIZE_MAX – m < n) 这个判断,为什么不用m + n > SIZE_MAX呢?因为,如果 m + n 溢出后,就被截断了,所以表达式恒真,也就检测不出来了。另外,这个表达式中,m和n分别会被提升为unsigned。
但是上面的代码是错的,因为:
1)检查的太晚了,if之前编译器的undefined行为就已经出来了(你不知道什么会发生)。
2)就像前面说的一样,(SIZE_MAX – m < n) 可能会被编译器优化掉。
3)另外,SIZE_MAX是size_t的最大值,size_t在64位系统下是64位的,严谨点应该用INT_MAX或是UINT_MAX
所以,正确的代码应该是下面这样:
|
1
2
3
4
5
6
7
8
9
|
void
foo(
int
m,
int
n)
{
size_t
s = 0;
if
( m>0 && n>0 && ( UINT_MAX - m < n ) ){
//error handling...
return
;
}
s = (
size_t
)m + (
size_t
)n;
}
|
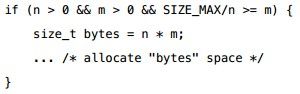
在《苹果安全编码规范》(PDF)中,第28页的代码中:
如果n和m都是signed int,那么这段代码是错的。正确的应该像上面的那个例子一样,至少要在n*m时要把 n 和 m 给 cast 成 size_t。因为,n*m可能已经溢出了,已经undefined了,undefined的代码转成size_t已经没什么意义了。(如果m和n是unsigned int,也会溢出),上面的代码仅在m和n是size_t的时候才有效。
不管怎么说,《苹果安全编码规范》绝对值得你去读一读。
二分取中搜索算法中的溢出
我们再来看一个二分取中搜索算法(binary search),大多数人都会写成下面这个样子:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
int
binary_search(
int
a[],
int
len,
int
key)
{
int
low = 0;
int
high = len - 1;
while
( low<=high ) {
int
mid = (low + high)/2;
if
(a[mid] == key) {
return
mid;
}
if
(key < a[mid]) {
high = mid - 1;
}
else
{
low = mid + 1;
}
}
return
-1;
}
|
上面这个代码中,你可能会有这样的想法:
1) 我们应该用size_t来做len, low, high, mid这些变量的类型。没错,应该是这样的。但是如果这样,你要小心第四行 int high = len -1; 如果len为0,那么就“high大发了”。
2) 无论你用不用size_t。我们在计算mid = (low+high)/2; 的时候,(low + high) 都可以溢出。正确的写法应该是:
|
1
|
int
mid = low + (high - low)/2;
|
上溢出和下溢出的检查
前面的代码只判断了正数的上溢出overflow,没有判断负数的下溢出underflow。让们来看看怎么判断:
对于加法,还好。
|
1
2
3
4
5
6
7
8
9
10
11
|
#include <limits.h>
void
f(
signed
int
si_a,
signed
int
si_b) {
signed
int
sum;
if
(((si_b > 0) && (si_a > (INT_MAX - si_b))) ||
((si_b < 0) && (si_a < (INT_MIN - si_b)))) {
/* Handle error */
return
;
}
sum = si_a + si_b;
}
|
对于乘法,就会很复杂(下面的代码太夸张了):
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
void
func(
signed
int
si_a,
signed
int
si_b)
{
signed
int
result;
if
(si_a > 0) {
/* si_a is positive */
if
(si_b > 0) {
/* si_a and si_b are positive */
if
(si_a > (INT_MAX / si_b)) {
/* Handle error */
}
}
else
{
/* si_a positive, si_b nonpositive */
if
(si_b < (INT_MIN / si_a)) {
/* Handle error */
}
}
/* si_a positive, si_b nonpositive */
}
else
{
/* si_a is nonpositive */
if
(si_b > 0) {
/* si_a is nonpositive, si_b is positive */
if
(si_a < (INT_MIN / si_b)) {
/* Handle error */
}
}
else
{
/* si_a and si_b are nonpositive */
if
( (si_a != 0) && (si_b < (INT_MAX / si_a))) {
/* Handle error */
}
}
/* End if si_a and si_b are nonpositive */
}
/* End if si_a is nonpositive */
result = si_a * si_b;
}
|
更多的防止在操作中整型溢出的安全代码可以参看《INT32-C. Ensure that operations on signed integers do not result in overflow》